18.2.2 菱形的性质 习题课件(含答案)
文档属性
| 名称 | 18.2.2 菱形的性质 习题课件(含答案) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览





文档简介
(共17张PPT)
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.2 菱形
第1课时 菱形的性质
下页
上页
课前预习
预习新知
1.有一组邻边相等的平行四边形叫做菱形,
因此,菱形是特殊的平行四边形,它具有
平行四边形的所有性质
2.菱形是(填“是”或“不是”)轴对称图形,它
有两条对称轴,分别是它的两条对角线
所在的直线
3.菱形的性质:
1)菱形的四条边都相等
(2)菱形的两条对角线互相垂直,并且每
条对角线平分一组对角
4.菱形的两条对角线把菱形分成四个全等的
直角三角形,菱形的面积等于两条对角线
乘积的一半
当堂训练
巩固基础
知识点1菱形的性质
1.(莆田)菱形具有而一般平行四边形不具有的
性质是
A.对边相等
B.对角相等
对角线互相平分D.对角线互相垂直
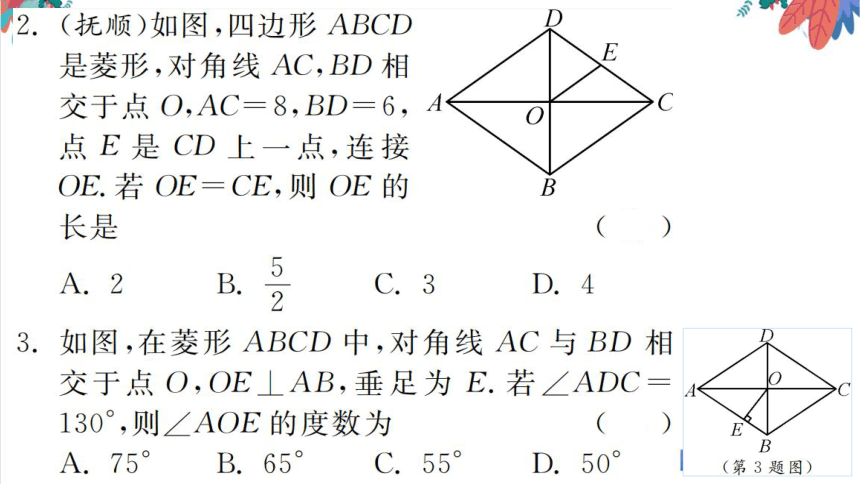
2.(抚顺)如图,四边形ABCD
是菱形,对角线AC,BD相
交于点O,AC=8,BD=6,A
点E是CD上一点,连接
OE.若OE=CE,则OE的
B
长是
(B
3.如图,在菱形ABCD中,对角线AC与BD相
交于点O,OE⊥AB,垂足为E.若∠ADC
130°,则∠AOE的度数为
B
A.75°
D.50°
C
B
(第3题图)
(广州)如图,若菱形ABCD的顶点A,B的坐
标分别为(3,0),(-2,0),点D在y轴上,则
点C的坐标是(—5,4)
在菱形ABCD中,∠A=30°.在同一平面内
以对角线BD为底边作顶角为120°的等腰
角形BDE,则∠EBC的度数为45或105°
B O
(第4题图)
如图,四边形ABCD是菱形,CE⊥AB交AB
的延长线于点E,CF⊥AD交AD的延长线于
点F.求证:DF=BE
证明:连接AC
∵四边形ABCD是菱形
AC平分∠DAB,CD=CB
CEAB CFAD
CF=CE.在Rt△CFD和A
B
CFECE
Rt△CEB中
CD=CB
Rt△CFD≌Rt△CEB(HL)
DE= BE
知识点2菱形的面积
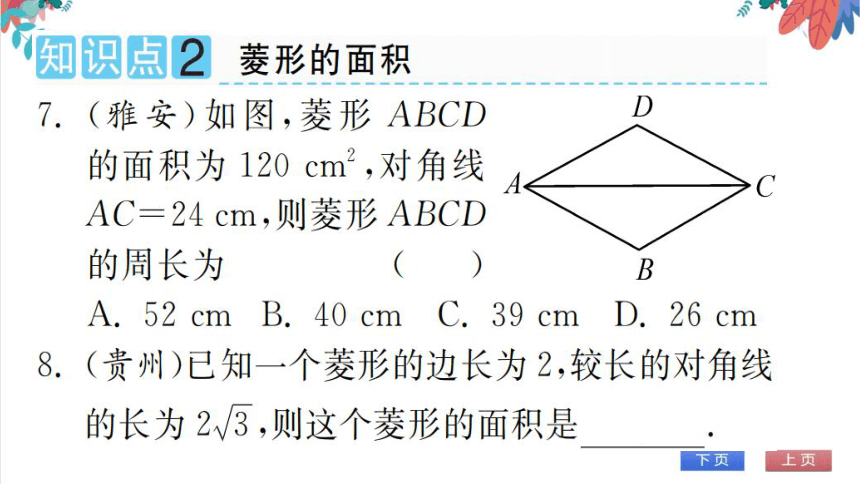
7.(雅安)如图,菱形ABCD
的面积为120cm2,对角线A
C
AC=24cm,则菱形ABCD
的周长为
(A)
B
A.52 cm B. 40 cm
39 cm d.26 cm
8.(贵州)已知一个菱形的边长为2,较长的对角线
的长为23,则这个菱形的面积是23
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.2 菱形
第1课时 菱形的性质
下页
上页
课前预习
预习新知
1.有一组邻边相等的平行四边形叫做菱形,
因此,菱形是特殊的平行四边形,它具有
平行四边形的所有性质
2.菱形是(填“是”或“不是”)轴对称图形,它
有两条对称轴,分别是它的两条对角线
所在的直线
3.菱形的性质:
1)菱形的四条边都相等
(2)菱形的两条对角线互相垂直,并且每
条对角线平分一组对角
4.菱形的两条对角线把菱形分成四个全等的
直角三角形,菱形的面积等于两条对角线
乘积的一半
当堂训练
巩固基础
知识点1菱形的性质
1.(莆田)菱形具有而一般平行四边形不具有的
性质是
A.对边相等
B.对角相等
对角线互相平分D.对角线互相垂直
2.(抚顺)如图,四边形ABCD
是菱形,对角线AC,BD相
交于点O,AC=8,BD=6,A
点E是CD上一点,连接
OE.若OE=CE,则OE的
B
长是
(B
3.如图,在菱形ABCD中,对角线AC与BD相
交于点O,OE⊥AB,垂足为E.若∠ADC
130°,则∠AOE的度数为
B
A.75°
D.50°
C
B
(第3题图)
(广州)如图,若菱形ABCD的顶点A,B的坐
标分别为(3,0),(-2,0),点D在y轴上,则
点C的坐标是(—5,4)
在菱形ABCD中,∠A=30°.在同一平面内
以对角线BD为底边作顶角为120°的等腰
角形BDE,则∠EBC的度数为45或105°
B O
(第4题图)
如图,四边形ABCD是菱形,CE⊥AB交AB
的延长线于点E,CF⊥AD交AD的延长线于
点F.求证:DF=BE
证明:连接AC
∵四边形ABCD是菱形
AC平分∠DAB,CD=CB
CEAB CFAD
CF=CE.在Rt△CFD和A
B
CFECE
Rt△CEB中
CD=CB
Rt△CFD≌Rt△CEB(HL)
DE= BE
知识点2菱形的面积
7.(雅安)如图,菱形ABCD
的面积为120cm2,对角线A
C
AC=24cm,则菱形ABCD
的周长为
(A)
B
A.52 cm B. 40 cm
39 cm d.26 cm
8.(贵州)已知一个菱形的边长为2,较长的对角线
的长为23,则这个菱形的面积是23
