18.2.3 正方形 习题课件(含答案)
文档属性
| 名称 | 18.2.3 正方形 习题课件(含答案) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览






文档简介
(共19张PPT)
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.3 正方形
下页
上页
课前预习
习新知
1.正方形的四条边都相等,四个角都是直角.因
此,正方形既是菱形,又是矩形,即有个角
是直角的菱形是正方形或者有组邻边
相等的矩形是正方形,它们可以作为正方形
的判定方法
2.正方形的对角线互相垂直平分且相等,每
条对角线平分一组对角
3.正方形是(填“是”或“不是”)轴对称图形
4.平行四边形、矩形、菱形、正方形的关系用下图
表示:
当堂训练
巩固基础
知识点1正方形的性质
平行四边形、矩形、菱形、正方形都具有的性质
是
A.对角线相等
B.对角线互相垂直
对角线互相平分
D.对角线互相垂直平分且相等
2.如图,点P是正方形ABCD的对角线BD上的
点,且BP=BC,则∠ACP的度数为(D
4
D
(第2题图)
(凉山)如图,在菱形ABCD中,∠B=60°,AB=4,
以AC为边长的正方形ACEF的周长为(
A.14
B.15
C.16
D.17
(宜昌)如图,正方形ABCD
的边长为1,点E,F分别是对
角线AC上的两点,EG⊥G
E
AB,EⅠ⊥AD,FH⊥AB,
FJ⊥AD,垂足分别为G,Ⅰ,
H,J,则图中阴影部分的面积B
等于
(B
A.1
B.
60°B
E
(第3题图)
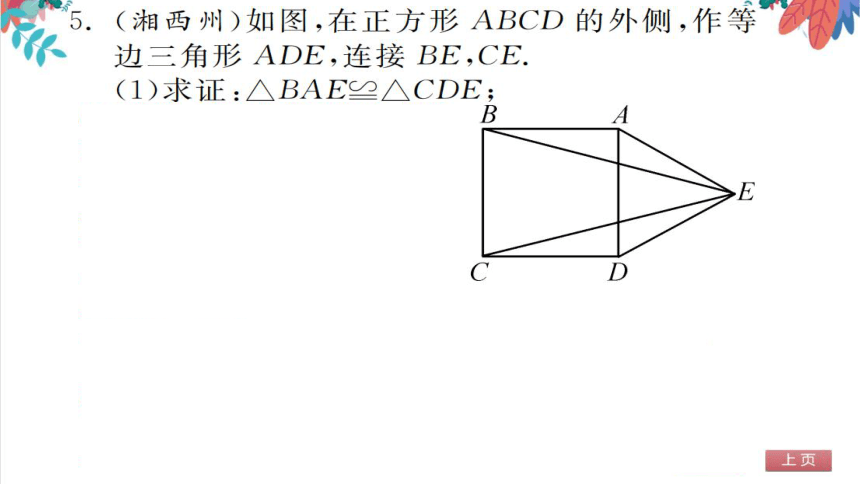
(1)证明:∵四边形ABCD是正B
方形
AB=CD,且∠BAD
E
CDA=90°
∴△ADE是等边三角形,
∴AE=DE,且∠EAD
∠EDA=60
∠BAE=150°,∠CDE=150°.∴∠BAE
CDE
AB=CD,
在△BAE和△CDE中,∠BAE=∠CDE,
AE-DE,
△BAE≌△CDE(SAS
知识点2正方形的判定
6.已知四边形ABCD中,∠A=∠B=∠C=90°,
如果添加一个条件,使四边形ABCD是正方
形,则这个条件可以是
A.∠D=90°
B. AB=CD
C. AD=BO
D. BO
D
7.如图,在△ABC中,∠ACB=90°,BC的垂直
平分线EF交BC于点D,交AB于点E,且
BE=BF.添加一个条件,仍
B
不能证明四边形BECF为正
方形的是
A. BC=AC
B.CF⊥BF
C. BD=DF
D. AC=BE
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.3 正方形
下页
上页
课前预习
习新知
1.正方形的四条边都相等,四个角都是直角.因
此,正方形既是菱形,又是矩形,即有个角
是直角的菱形是正方形或者有组邻边
相等的矩形是正方形,它们可以作为正方形
的判定方法
2.正方形的对角线互相垂直平分且相等,每
条对角线平分一组对角
3.正方形是(填“是”或“不是”)轴对称图形
4.平行四边形、矩形、菱形、正方形的关系用下图
表示:
当堂训练
巩固基础
知识点1正方形的性质
平行四边形、矩形、菱形、正方形都具有的性质
是
A.对角线相等
B.对角线互相垂直
对角线互相平分
D.对角线互相垂直平分且相等
2.如图,点P是正方形ABCD的对角线BD上的
点,且BP=BC,则∠ACP的度数为(D
4
D
(第2题图)
(凉山)如图,在菱形ABCD中,∠B=60°,AB=4,
以AC为边长的正方形ACEF的周长为(
A.14
B.15
C.16
D.17
(宜昌)如图,正方形ABCD
的边长为1,点E,F分别是对
角线AC上的两点,EG⊥G
E
AB,EⅠ⊥AD,FH⊥AB,
FJ⊥AD,垂足分别为G,Ⅰ,
H,J,则图中阴影部分的面积B
等于
(B
A.1
B.
60°B
E
(第3题图)
(1)证明:∵四边形ABCD是正B
方形
AB=CD,且∠BAD
E
CDA=90°
∴△ADE是等边三角形,
∴AE=DE,且∠EAD
∠EDA=60
∠BAE=150°,∠CDE=150°.∴∠BAE
CDE
AB=CD,
在△BAE和△CDE中,∠BAE=∠CDE,
AE-DE,
△BAE≌△CDE(SAS
知识点2正方形的判定
6.已知四边形ABCD中,∠A=∠B=∠C=90°,
如果添加一个条件,使四边形ABCD是正方
形,则这个条件可以是
A.∠D=90°
B. AB=CD
C. AD=BO
D. BO
D
7.如图,在△ABC中,∠ACB=90°,BC的垂直
平分线EF交BC于点D,交AB于点E,且
BE=BF.添加一个条件,仍
B
不能证明四边形BECF为正
方形的是
A. BC=AC
B.CF⊥BF
C. BD=DF
D. AC=BE
