20.2 数据的波动程度(第1课时)习题课件(含答案)
文档属性
| 名称 | 20.2 数据的波动程度(第1课时)习题课件(含答案) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
20.2 数据的波动程度
第1课时 方差的意义
下页
上页
课前预习
预习新知
1.方差:设有n个数据x1,x2,…,xn,它们的平均数
为x,我们把(x1-x)2,(x2-x)2,…,(xn-x)2的
平均数叫做这组数据的方差,用s2表示.即
+…+(
72
2.方差是反映一组数据的波动大小的特征
量,方差越大,数据的波动性也越大
知织点1方差的计算
1.(自贡)在一次数学测试后,随机抽取九年级
(3)班5名学生的成绩(单位:分)如下:80,98,
98,83,91,下列关于这组数据的说法错误的是
A.众数是98
B.平均数是90
C.中位数是91
D.方差是56
2.(襄阳)一组数据3,2,3,4,x的平均数是3,则
它的方差是0.4
个样本的方差s2
20)2+(
20)
(x10-20)2],那么这个样本的容量
是10,式子中的20表示样本平均数
知识点2方差的应用
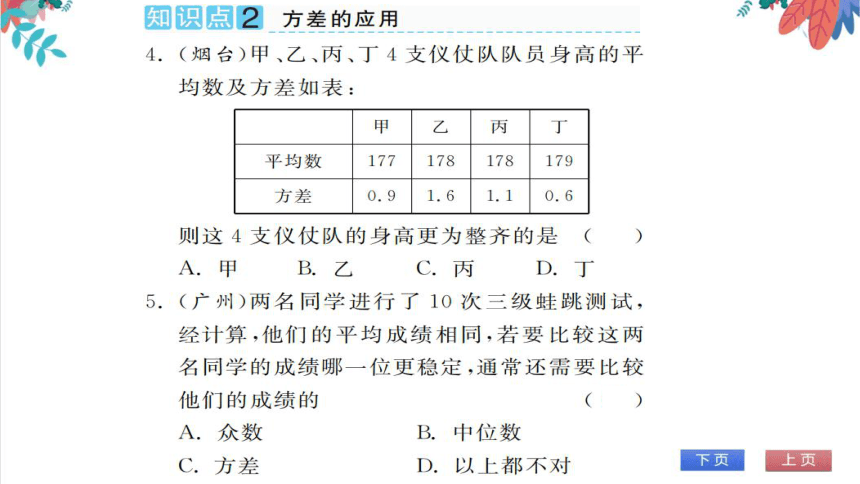
(烟台)甲、乙、丙、丁4支仪仗队队员身高的平
均数及方差如表
甲乙丙丁
平均数
77
78
78
79
方差
0.9
6
10.6
则这4支仪仗队的身高更为整齐的是(D
C.丙
5.(广州)两名同学进行了10次三级蛙跳测试,
经计算,他们的平均成绩相同,若要比较这两
名同学的成绩哪一位更稳定,通常还需要比较
他们的成绩的
A.众数
B.中位数
C.方差
D.以上都不对
(泰州)某科普小组有5名成员,身高(单位:cm
分别为:160,165,170,163,167.增加1名身高为
165cm的成员后,现科普小组成员的身高与原来
相比,下列说法正确的是
CC
A.平均数不变,方差不变
B.平均数不变,方差变大
C.平均数不变,方差变小
D.平均数变小,方差不变
(张家界)若一组数据a1,a2,a3的平均数为4,
方差为3,那么数据a1+2,a2+2,a3+2的平
均数和方差分别是
( B
C.3,4
D.6,5
8.(大庆)甲、乙两人进行飞镖比赛,每人各投5
次,所得平均环数相等,其中甲所得环数的方
差为15,乙所得环数如下:0,1,5,9,10,那么
成绩较稳定的是甲(填“甲”或“乙”)
9.(黄冈)需要对一批排球的质量进行检查,其中
质量超过标准的克数记为正,不足标准的克数
记为负,现抽取8个排球,通过检测得到如下
数据(单位:g):+1,-2,+1,0,+2,-3,0,+1,
这组数据的方差是2.5
10.甲、乙两人在5次打靶测试中命中的环数如下
甲:8,8,7,8,9;乙:5,9,7,10,9.
1)填写下表
平均数众数中位数方差
甲
0.4
乙
(2)教练根据这5次成绩,选择甲参加射击比
赛,教练的理由是什么
解:因为他们的平均数相等,而甲的方差小
发挥比较稳定,所以选择甲参加射击比赛
20.2 数据的波动程度
第1课时 方差的意义
下页
上页
课前预习
预习新知
1.方差:设有n个数据x1,x2,…,xn,它们的平均数
为x,我们把(x1-x)2,(x2-x)2,…,(xn-x)2的
平均数叫做这组数据的方差,用s2表示.即
+…+(
72
2.方差是反映一组数据的波动大小的特征
量,方差越大,数据的波动性也越大
知织点1方差的计算
1.(自贡)在一次数学测试后,随机抽取九年级
(3)班5名学生的成绩(单位:分)如下:80,98,
98,83,91,下列关于这组数据的说法错误的是
A.众数是98
B.平均数是90
C.中位数是91
D.方差是56
2.(襄阳)一组数据3,2,3,4,x的平均数是3,则
它的方差是0.4
个样本的方差s2
20)2+(
20)
(x10-20)2],那么这个样本的容量
是10,式子中的20表示样本平均数
知识点2方差的应用
(烟台)甲、乙、丙、丁4支仪仗队队员身高的平
均数及方差如表
甲乙丙丁
平均数
77
78
78
79
方差
0.9
6
10.6
则这4支仪仗队的身高更为整齐的是(D
C.丙
5.(广州)两名同学进行了10次三级蛙跳测试,
经计算,他们的平均成绩相同,若要比较这两
名同学的成绩哪一位更稳定,通常还需要比较
他们的成绩的
A.众数
B.中位数
C.方差
D.以上都不对
(泰州)某科普小组有5名成员,身高(单位:cm
分别为:160,165,170,163,167.增加1名身高为
165cm的成员后,现科普小组成员的身高与原来
相比,下列说法正确的是
CC
A.平均数不变,方差不变
B.平均数不变,方差变大
C.平均数不变,方差变小
D.平均数变小,方差不变
(张家界)若一组数据a1,a2,a3的平均数为4,
方差为3,那么数据a1+2,a2+2,a3+2的平
均数和方差分别是
( B
C.3,4
D.6,5
8.(大庆)甲、乙两人进行飞镖比赛,每人各投5
次,所得平均环数相等,其中甲所得环数的方
差为15,乙所得环数如下:0,1,5,9,10,那么
成绩较稳定的是甲(填“甲”或“乙”)
9.(黄冈)需要对一批排球的质量进行检查,其中
质量超过标准的克数记为正,不足标准的克数
记为负,现抽取8个排球,通过检测得到如下
数据(单位:g):+1,-2,+1,0,+2,-3,0,+1,
这组数据的方差是2.5
10.甲、乙两人在5次打靶测试中命中的环数如下
甲:8,8,7,8,9;乙:5,9,7,10,9.
1)填写下表
平均数众数中位数方差
甲
0.4
乙
(2)教练根据这5次成绩,选择甲参加射击比
赛,教练的理由是什么
解:因为他们的平均数相等,而甲的方差小
发挥比较稳定,所以选择甲参加射击比赛
