第十八章 平行四边形 整合与提高 习题课件(含答案)
文档属性
| 名称 | 第十八章 平行四边形 整合与提高 习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:32 | ||
图片预览





文档简介
(共17张PPT)
第十八章 整合与提高
下页
上页
考点专训
考点1平行四边形的性质
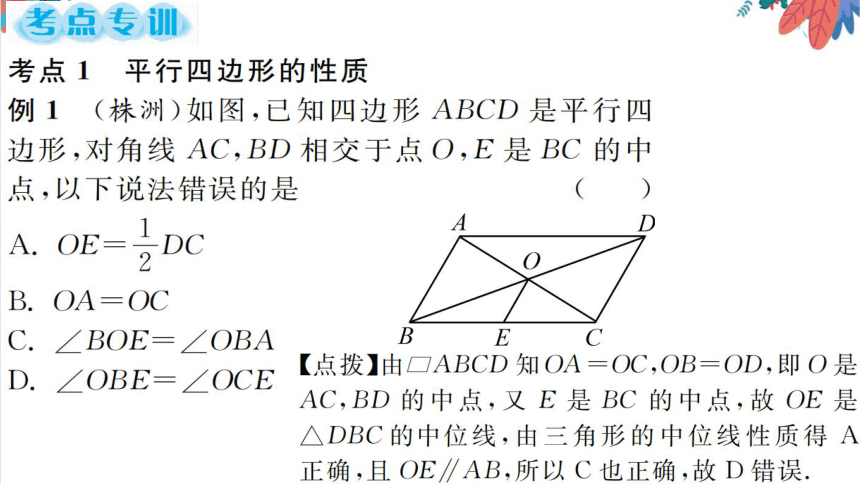
例1(株洲)如图,已知四边形ABCD是平行四
边形,对角线AC,BD相交于点O,E是BC的中
,以下说法错误的是
A OE
DO
B OA=OC
∠BOE=∠OBA
E
D.∠OBE
OCE
考点2平行四边形的判定
例2在四边形ABCD中,对角线AC,BD相交
于点O,下列条件中不能判定四边形ABCD是平
行四边形的是
A.OA=OC,OB=ODB.AD∥BC,AB∥DC
C.AD∥BC,AD=BCD.AB∥DC,AD=BC
【点拨】根据平行四边形的判定定理逐一排查可
得答案
例3已知平面直角坐标系内有四个点O(0,0)
A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点
的四边形是平行四边形,则x=4或-2
点拨】以O,A,B,C为顶点的四边形是平行四边
考点3三角形的中位线
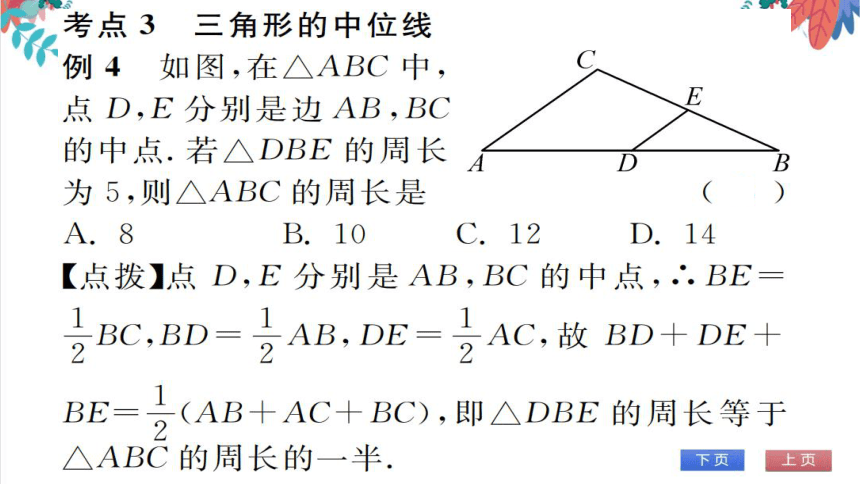
例4如图,在△ABC中,
点D,E分别是边AB,BC
的中点.若△DBE的周长
为5,则△ABC的周长是
( B
B.10
D.14
【点拨】点D,E分别是AB,BC的中点,∴BE
BC. BD
AB,DE=AC,故BD+DE
BE=(AB+AC+BC),即△DBE的周长等于
考点4特殊平行四边形的性质与判定
例5(酒泉)如图,在□ ABCD B
中,AB=3cm,BC=5cm,
B=60°,G是CD的中点,E
是边AD上的一动点,EG的延
E D
长线与BC的延长线相交于点F,连接CE,DF
(1)证明:∵四边形ABCD是平行四边形
∴BC∥AD
∠FCG=∠EDG,∠CFG=∠DEG
G是CD的中点,∴CG=DG
△CGF≌△DGE(AAS).∴GF=EG
又∵CG=DG,∴四边形CEDF是平行四边形
(2)①当AE
cm时,四边形CEDF是矩形
②当AE=2cm时,四边形CEDF是菱形
【点拨】(1)∵G是CD的中点,∴要证明四边形
CEDF是平行四边形,可以考虑证明EG=GF,由
已知条件易证△CGF≌△DGE
(2)①当∠CED=90°时,由(1)知□CEDF为矩
形,在□ABCD中,AB=CD=3cm,∠ADC
∠B=60°,得∠ECD=30°,故DE
CD
cm.再由AE=AD-DE求得.②当EC=DE
优生特训
将一张矩形纸片折叠一次,使折痕平分这个矩
形的面积,则这样的折法有
A.2种B.3种C.4种D.无数种
如图,E,F,G,H分别是BD,BC,AC,AD的
中点,且AB=CD,下列结论:①EG⊥FH;
②四边形EFGH是矩形;③HF平分∠EHG;
④EG=(BC-AD);⑤四边形EFGH是菱
形.其中正确的有
A
B.2个C.3个D.4个
第十八章 整合与提高
下页
上页
考点专训
考点1平行四边形的性质
例1(株洲)如图,已知四边形ABCD是平行四
边形,对角线AC,BD相交于点O,E是BC的中
,以下说法错误的是
A OE
DO
B OA=OC
∠BOE=∠OBA
E
D.∠OBE
OCE
考点2平行四边形的判定
例2在四边形ABCD中,对角线AC,BD相交
于点O,下列条件中不能判定四边形ABCD是平
行四边形的是
A.OA=OC,OB=ODB.AD∥BC,AB∥DC
C.AD∥BC,AD=BCD.AB∥DC,AD=BC
【点拨】根据平行四边形的判定定理逐一排查可
得答案
例3已知平面直角坐标系内有四个点O(0,0)
A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点
的四边形是平行四边形,则x=4或-2
点拨】以O,A,B,C为顶点的四边形是平行四边
考点3三角形的中位线
例4如图,在△ABC中,
点D,E分别是边AB,BC
的中点.若△DBE的周长
为5,则△ABC的周长是
( B
B.10
D.14
【点拨】点D,E分别是AB,BC的中点,∴BE
BC. BD
AB,DE=AC,故BD+DE
BE=(AB+AC+BC),即△DBE的周长等于
考点4特殊平行四边形的性质与判定
例5(酒泉)如图,在□ ABCD B
中,AB=3cm,BC=5cm,
B=60°,G是CD的中点,E
是边AD上的一动点,EG的延
E D
长线与BC的延长线相交于点F,连接CE,DF
(1)证明:∵四边形ABCD是平行四边形
∴BC∥AD
∠FCG=∠EDG,∠CFG=∠DEG
G是CD的中点,∴CG=DG
△CGF≌△DGE(AAS).∴GF=EG
又∵CG=DG,∴四边形CEDF是平行四边形
(2)①当AE
cm时,四边形CEDF是矩形
②当AE=2cm时,四边形CEDF是菱形
【点拨】(1)∵G是CD的中点,∴要证明四边形
CEDF是平行四边形,可以考虑证明EG=GF,由
已知条件易证△CGF≌△DGE
(2)①当∠CED=90°时,由(1)知□CEDF为矩
形,在□ABCD中,AB=CD=3cm,∠ADC
∠B=60°,得∠ECD=30°,故DE
CD
cm.再由AE=AD-DE求得.②当EC=DE
优生特训
将一张矩形纸片折叠一次,使折痕平分这个矩
形的面积,则这样的折法有
A.2种B.3种C.4种D.无数种
如图,E,F,G,H分别是BD,BC,AC,AD的
中点,且AB=CD,下列结论:①EG⊥FH;
②四边形EFGH是矩形;③HF平分∠EHG;
④EG=(BC-AD);⑤四边形EFGH是菱
形.其中正确的有
A
B.2个C.3个D.4个
