第十九章 一次函数 复习整合与提高 习题课件(含答案)
文档属性
| 名称 | 第十九章 一次函数 复习整合与提高 习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:32 | ||
图片预览






文档简介
(共18张PPT)
第十九章 整合与提高
下页
上页
考点专训
考点1函数的有关概念及图象
例1(黃冈)在函数y
中,自变量x的
取值范围是
B. x
4
C.x≥-4且x≠0
D.x>0且x≠-4
【点拨】由题意可得,根据二次根式的概念和分式
的概念,自变量x的取值范围为x十4≥0且x≠
0,即可求得
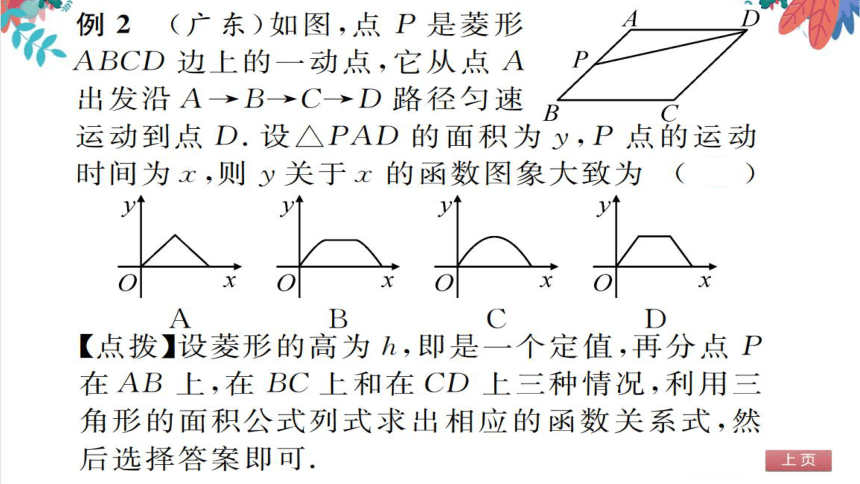
例2(广东)如图,点P是菱形
ABCD边上的一动点,它从点A
出发沿A→B→>C→>D路径匀速
运动到点D.设△PAD的面积为y,P点的运动
时间为x,则y关于x的函数图象大致为(D)
考点2一次函数的图象和性质
例3如图,直线y
x轴、y轴分别交于点A和点
D
B,点C,D分别为线段AB,OB
的中点,点P为OA上一动点,A4
PC+PD值最小时点P的坐标为
A.(-3,0)
B.(-6,0)
例4(枣庄)如图,直线y=2x+4
与x,y轴分别交于A,B两点,以
OB为边在y轴右侧作等边
△OBC,将点C向左平移,使其对
应点C′恰好落在直线AB上,则点
C的坐标为
1,2)
【点拨】由已知先求出点B的坐标为(0,4),则
OB=4,根据等腰三角形“三线合一”的性质,且
CC垂直平分OB,∴C,C点的纵坐标为2,把y
2代入y=2x+4,得x
,即C(-1,2)
考点3确定一次函数的解析式
例5若一次函数y=kx+b(k≠0)的图象经过
A(1,3),B(0,-2)两点,则这个一次函数的解
析式是y=5x-2
【点拨】根据待定系数法把A,B两点的坐标代入
kx+b中可得关于k,b的方程组,解这个方程
组得k,b的值,即可得到一次函数的解析式
考点4一次函数与一元一次不等式
例6一次函数y=kx+b与y2=x+a的图象如
图所示,则kx+b>x+a的解集为x-2
【点拨】先确定两直线的交点,y={x+b+yy2=x+a
可知x=-2时,y1=y2,根据
图象上方的函数值大于下方的
函数值可知,kx+b>x+a就
是交点左侧的图象,故x<-2
考点5一次函数的实际应用
某果园计划新购进A,B两个品381
例7(荆州)为更新果树品种
60
种的果树苗栽植培育,若计划购
进这两种树苗共45棵,其中A
2040x/棵
种树苗的单价为7元/棵,购买B
种树苗所需费用y(单位:元)与购买棵数x之间
存在如图所示的函数关系
(1)求y与x的函数解析式;
第十九章 整合与提高
下页
上页
考点专训
考点1函数的有关概念及图象
例1(黃冈)在函数y
中,自变量x的
取值范围是
B. x
4
C.x≥-4且x≠0
D.x>0且x≠-4
【点拨】由题意可得,根据二次根式的概念和分式
的概念,自变量x的取值范围为x十4≥0且x≠
0,即可求得
例2(广东)如图,点P是菱形
ABCD边上的一动点,它从点A
出发沿A→B→>C→>D路径匀速
运动到点D.设△PAD的面积为y,P点的运动
时间为x,则y关于x的函数图象大致为(D)
考点2一次函数的图象和性质
例3如图,直线y
x轴、y轴分别交于点A和点
D
B,点C,D分别为线段AB,OB
的中点,点P为OA上一动点,A4
PC+PD值最小时点P的坐标为
A.(-3,0)
B.(-6,0)
例4(枣庄)如图,直线y=2x+4
与x,y轴分别交于A,B两点,以
OB为边在y轴右侧作等边
△OBC,将点C向左平移,使其对
应点C′恰好落在直线AB上,则点
C的坐标为
1,2)
【点拨】由已知先求出点B的坐标为(0,4),则
OB=4,根据等腰三角形“三线合一”的性质,且
CC垂直平分OB,∴C,C点的纵坐标为2,把y
2代入y=2x+4,得x
,即C(-1,2)
考点3确定一次函数的解析式
例5若一次函数y=kx+b(k≠0)的图象经过
A(1,3),B(0,-2)两点,则这个一次函数的解
析式是y=5x-2
【点拨】根据待定系数法把A,B两点的坐标代入
kx+b中可得关于k,b的方程组,解这个方程
组得k,b的值,即可得到一次函数的解析式
考点4一次函数与一元一次不等式
例6一次函数y=kx+b与y2=x+a的图象如
图所示,则kx+b>x+a的解集为x-2
【点拨】先确定两直线的交点,y={x+b+yy2=x+a
可知x=-2时,y1=y2,根据
图象上方的函数值大于下方的
函数值可知,kx+b>x+a就
是交点左侧的图象,故x<-2
考点5一次函数的实际应用
某果园计划新购进A,B两个品381
例7(荆州)为更新果树品种
60
种的果树苗栽植培育,若计划购
进这两种树苗共45棵,其中A
2040x/棵
种树苗的单价为7元/棵,购买B
种树苗所需费用y(单位:元)与购买棵数x之间
存在如图所示的函数关系
(1)求y与x的函数解析式;
