第十七章 勾股定理 整合与提高 习题课件(含答案)
文档属性
| 名称 | 第十七章 勾股定理 整合与提高 习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:32 | ||
图片预览





文档简介
(共14张PPT)
第十七章 整合与提高
下页
上页
考点专训
考点1勾股定理及其应用
例1在Rt△ABC中,AB=12,AC=6,则BC
63或65
点拨】利用勾股定理在直角三角形中已知任意
两边长可求第三边长,但必颏分清直角边、斜边,
本题并未指明,故要分情况给予求解,因为AB>
AC,所以分两种情况:(1)当AB为斜边时,则
BC=√AB2=AC=63;(2)当BC为斜边时,
Bc
AC2+AB2=6√5
考点2勾股定理的逆定理及其应用
例2(达州)如图,在5×5的正方形网格中,从
在格点上的点A,B,C,D中任取三点,能构成直
角三角形的个数是3
【点拨】从A,B,C,D中任取
点有A,B,C;A,B,D;A,C,D;
B,C,D四种情况,首先利用勾BD
C
股定理求出AB2,BC2,AC,
AD2,CD),BD2,再看有两边的
平方和等于第三边的平方,进而得到答案
例3如图,在△ABC中,D为BC边上一点,
AB=15,BD=9,AD=12,AC=13
(1)求证:AD⊥BC;
(2)求△ABC的面积
【点拔】已知△ABD三边的长度,利用勾股定理的
逆定理先证出AD⊥BC,然后在Rt△ADC中,利
用勾股定理求出CD,最后根据三角形面积公式
得出△ABC的面积
(1)证明:122+92=152
即AD2+BD2=AB2
△ABD为直角三角形,且
∠ADB=90°
B
∴ADBC
(2)解:由(1)知,∠ADB=90
则∠ADC=90°,△ACD为直角三角形
DCENACZ-AD
∴BC=BD+DC=9+5=14
°·△ABC
BC·AD
14×12=84
优生特训
以下列各组数为边长,能组成直角三角形的有
①1,2,:3’4
③32,42,52;④9,40,41
⑤m2+n2,m2-n2,2mn(m
0).
A.5个B.4个C.3个D.2个
如图,数轴上点A,B分别对应1,2,过点B作
PQ⊥AB,以点B为圆心,AB长为半径画弧,
交PQ于点C,以原点O为圆心,OC长为半径
画弧,交数轴于点M,则点M对应的数是
C B
A.3
B.√5
B
O12M3
(第2题图)
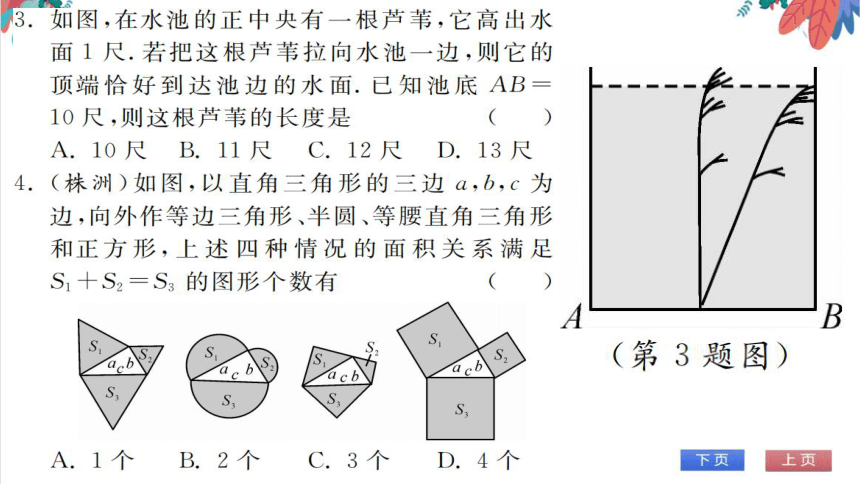
3.如图,在水池的正中央有一根芦苇,它高出水
面1尺.若把这根芦苇拉向水池一边,则它的
顶端恰好到达池边的水面.已知池底AB
10尺,则这根芦苇的长度是
D
A.10尺B.11尺C.12尺D.13尺
4.(株洲)如图,以直角三角形的三边a,b,c为
边,向外作等边三角形、半圆、等腰直角三角形
和正方形,上述四种情况的面积关系满足
S1+S2=S3的图形个数有
D
A.1个B.2个C.3个D.4个
第十七章 整合与提高
下页
上页
考点专训
考点1勾股定理及其应用
例1在Rt△ABC中,AB=12,AC=6,则BC
63或65
点拨】利用勾股定理在直角三角形中已知任意
两边长可求第三边长,但必颏分清直角边、斜边,
本题并未指明,故要分情况给予求解,因为AB>
AC,所以分两种情况:(1)当AB为斜边时,则
BC=√AB2=AC=63;(2)当BC为斜边时,
Bc
AC2+AB2=6√5
考点2勾股定理的逆定理及其应用
例2(达州)如图,在5×5的正方形网格中,从
在格点上的点A,B,C,D中任取三点,能构成直
角三角形的个数是3
【点拨】从A,B,C,D中任取
点有A,B,C;A,B,D;A,C,D;
B,C,D四种情况,首先利用勾BD
C
股定理求出AB2,BC2,AC,
AD2,CD),BD2,再看有两边的
平方和等于第三边的平方,进而得到答案
例3如图,在△ABC中,D为BC边上一点,
AB=15,BD=9,AD=12,AC=13
(1)求证:AD⊥BC;
(2)求△ABC的面积
【点拔】已知△ABD三边的长度,利用勾股定理的
逆定理先证出AD⊥BC,然后在Rt△ADC中,利
用勾股定理求出CD,最后根据三角形面积公式
得出△ABC的面积
(1)证明:122+92=152
即AD2+BD2=AB2
△ABD为直角三角形,且
∠ADB=90°
B
∴ADBC
(2)解:由(1)知,∠ADB=90
则∠ADC=90°,△ACD为直角三角形
DCENACZ-AD
∴BC=BD+DC=9+5=14
°·△ABC
BC·AD
14×12=84
优生特训
以下列各组数为边长,能组成直角三角形的有
①1,2,:3’4
③32,42,52;④9,40,41
⑤m2+n2,m2-n2,2mn(m
0).
A.5个B.4个C.3个D.2个
如图,数轴上点A,B分别对应1,2,过点B作
PQ⊥AB,以点B为圆心,AB长为半径画弧,
交PQ于点C,以原点O为圆心,OC长为半径
画弧,交数轴于点M,则点M对应的数是
C B
A.3
B.√5
B
O12M3
(第2题图)
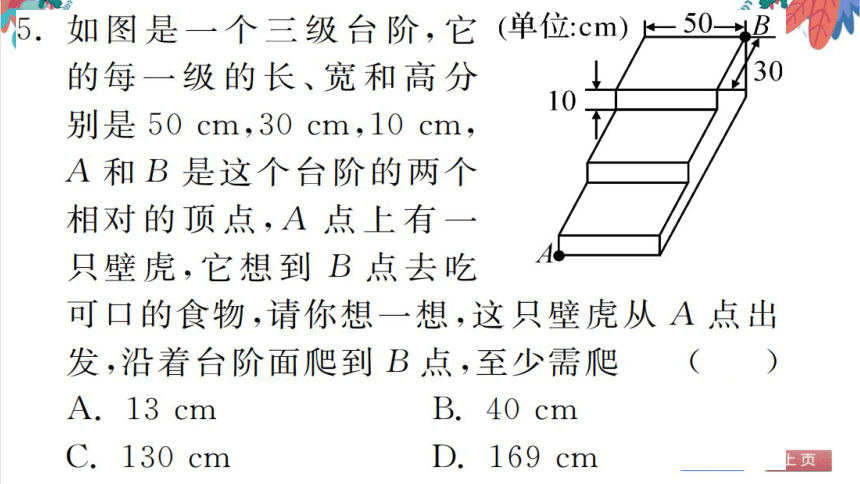
3.如图,在水池的正中央有一根芦苇,它高出水
面1尺.若把这根芦苇拉向水池一边,则它的
顶端恰好到达池边的水面.已知池底AB
10尺,则这根芦苇的长度是
D
A.10尺B.11尺C.12尺D.13尺
4.(株洲)如图,以直角三角形的三边a,b,c为
边,向外作等边三角形、半圆、等腰直角三角形
和正方形,上述四种情况的面积关系满足
S1+S2=S3的图形个数有
D
A.1个B.2个C.3个D.4个
