2022年华东师大版九年级数学下册第27章 圆 单元训练卷(Word版含答案)
文档属性
| 名称 | 2022年华东师大版九年级数学下册第27章 圆 单元训练卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 497.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览



文档简介
华东师大版九年级数学下册
第27章 圆
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
A.点P在⊙O外 B.点P在⊙O上
C.点P在⊙O内 D.无法确定
2. 如图,在平面直角坐标系中,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为上一点(不与O,A两点重合),则cos C的值为( )
A. B. C. D.
3. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影=( )
A.π B.2π C.π D.π
4. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A.2 B.3 C.4 D.5
5. 如图,已知⊙O的直径AB⊥弦CD于点E.则下列结论中一定正确的是( )
A.AE=OE B.CE=DE C.OE=CE D.∠AOC=60°
6. 如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
A. B. C. D.
7. 如图,点A,B,C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,若∠DCE=40°,则∠ACB的度数为( )
A.140° B.70° C.110° D.80°
8. 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,到半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.3π B.4π C.5π D.6π
9.如图,圆内接正六边形的边长为4,以其各边为直径作半圆,则图中阴影部分的面积为( )
A.24-4π B.12+4π C.24+8π D.24+4π
10. 如图,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC,下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD:S△BOC=AD2:AO2;④OD:OC=DE:EC;⑤OD2=DE·CD.正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共6小题,4*6=24)
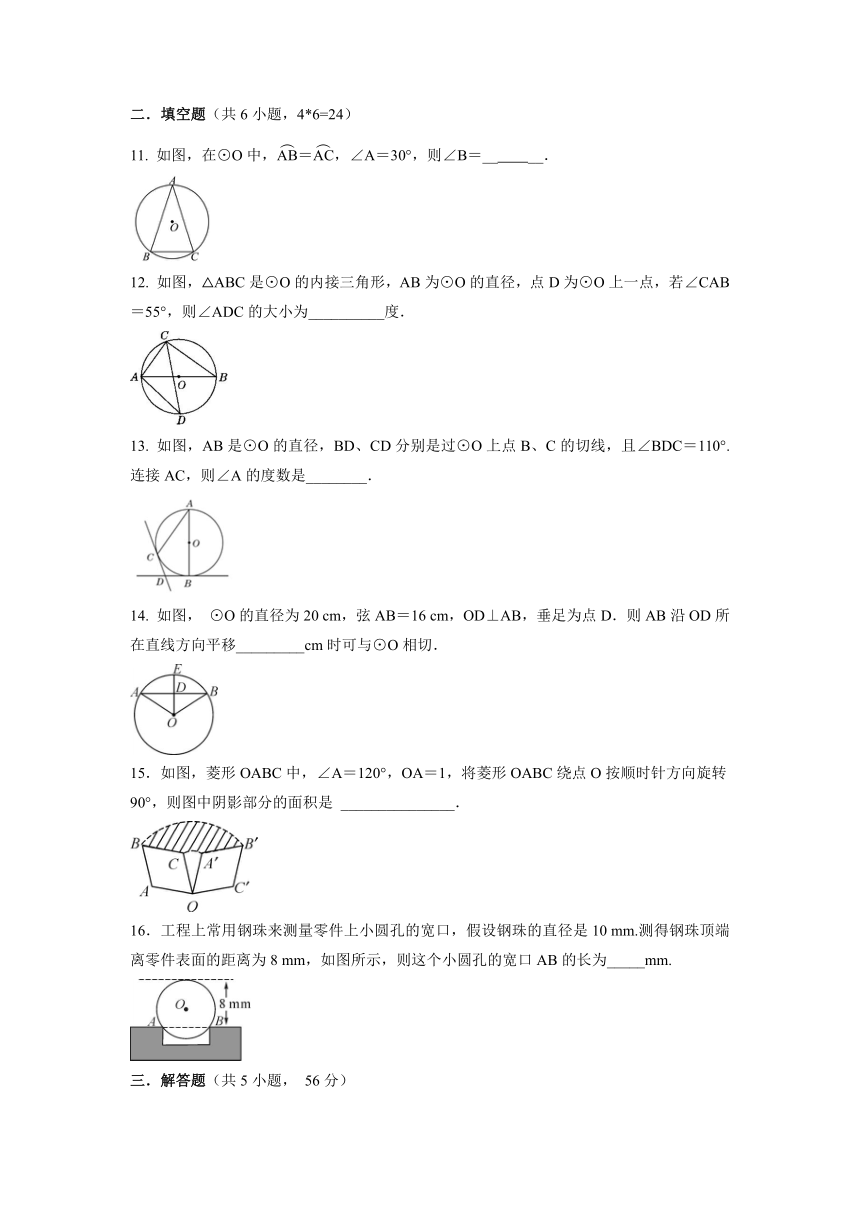
11. 如图,在⊙O中,=,∠A=30°,则∠B=__ __.
12. 如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D为⊙O上一点,若∠CAB=55°,则∠ADC的大小为__________度.
13. 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=110°.连接AC,则∠A的度数是________.
14. 如图, ⊙O的直径为20 cm,弦AB=16 cm,OD⊥AB,垂足为点D.则AB沿OD所在直线方向平移_________cm时可与⊙O相切.
15.如图,菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O按顺时针方向旋转90°,则图中阴影部分的面积是 _______________.
16.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10 mm.测得钢珠顶端离零件表面的距离为8 mm,如图所示,则这个小圆孔的宽口AB的长为_____mm.
三.解答题(共5小题, 56分)
17.(6分) 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面图;(要求尺规作图,保留作图痕迹,不写作法)
(2)若有水部分的水面宽AB=32 cm,水最深处的地方高度为8 cm,求这个圆形截面的半径.
18.(8分) 如图,圆O通过五边形OABCD的四个顶点.若∠AOD=150°,∠A=75°,∠D=60°,求证:BC=DC.
19.(8分) 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=10,BC=6,求CD的长.
20.(10分) 如图, A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连结CD,AD.
(1)求证:DB平分∠ADC;
(2)若BE=3,ED=6,求AB的长.
21.(12分) 如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连结OF.
(1)求证:OD∥BE;
(2)猜想:OF与CD有何数量关系?并说明理由.
22.(12分) 如图①,已知⊙O是△ADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
(1)求证:AC=BC;
(2)如图②,在图①的基础上作⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH∥BC,求∠ACF的度数;
(3)在(2)的条件下,若△ABD的面积为6,△ABD与△ABC的面积比为2∶9,求CD的长.
参考答案
1-5CADAB 6-10ACCAC
11.75°
12.35
13.35°
14.4或16
15.π-
16.8
17.解:(1)如图所示.
(2)连结OA,易知点D为AB的中点,∵AB=32 cm,∴AD=AB=16 cm,设这个圆形截面的半径为x cm,又∵CD=8 cm,∴OD=(x-8) cm,在Rt△OAD中,∵OD2+AD2=OA2,即(x-8)2+162=x2,解得x=20,∴圆形截面的半径为20 cm.
18. 证明:连结OB,OC.∵OA=OB=OC=OD,∴△OAB,△OBC,△OCD皆为等腰三角形.∵∠A=75°,∠D=60°,∴∠1=180°-2∠A=180°-2×75°=30°,∠2=180°-2∠D=180°-2×60°=60°.∵∠AOD=150°,∴∠3=∠AOD-∠1-∠2=150°-30°-60°=60°=∠2,∴BC=DC
19.(1)证明:连接AC,OC,如图,∵CD为切线,∴OC⊥CD,又∵CD⊥AD,∴OC∥AD,∴∠OCB=∠E,∵OB=OC,∴∠OCB=∠B,∴∠B=∠E,∴AE=AB
(2)解:∵AB为直径,∴∠ACB=90°,∴AC==8,∵AB=AE=10,AC⊥BE,∴CE=BC=6,∵CD·AE=AC·CE,∴CD==
20. 解:(1)∵AB=BC,∴=,∴∠ADB=∠BDC,∴DB平分∠ADC (2)由(1)可知,=,∴∠BAC=∠ADB,又∵∠ABE=∠ABD,∴△ABE∽△DBA,∴=,∵BE=3,ED=6,∴BD=9,∴AB2=BE·BD=3×9=27,∴AB=3
21.解:(1)连结OE,∵AM,DE是⊙O的切线,OA,OE是⊙O的半径,∴∠ADO=∠EDO,∠DAO=∠DEO=90°,∴∠AOD=∠EOD=∠AOE.∵∠ABE=∠AOE,∴∠AOD=∠ABE,∴OD∥BE
(2)OF=CD.理由如下:连结OC,∵BC,CE是⊙O的切线,OB,OE是⊙O半径,∴∠OBC=90°,∠OCB=∠OCE,同理:∠ADO=∠EDO.∵∠OAD+∠OBC=180°,∴AM∥BN,∴∠ADO+∠EDO+∠OCB+∠OCE=180°,∴∠EDO+∠OCE=90°,∴∠DOC=90°,在Rt△DOC中,∵F是DC的中点,∴OF=CD
22.解:(1)证明:∵DC平分∠ADB,∴∠ADC=∠BDC,∴=,∴AC=BC
(2)连接AO并延长交BC于点I,交⊙O于点J.∵AH是⊙O的切线,且AH∥BC,∴AI⊥BC.由垂径定理,得BI=IC,∴AI垂直平分BC,∴AB=AC=BC,∴△ABC是等边三角形,∠ABC=60°=∠F,∵FC是直径,∴∠FAC=90°,∴∠ACF=180°-90°-60°=30°
(3)过点D作DG⊥AB,∵△ABC为等边三角形,∠ACF=30°,∴AB⊥CF,∴AE=BE,∵S△ABC=AB2=27,∴AB=6,∴AE=3,CE=9,在Rt△AEO中,设EO=x,则AO=2x,∴AO2=AE2+OE2,∴(2x)2=(3)2+x2,∴x=3,∴⊙O的半径为6,∴CF=12,∵S△ABD=AB×DG×=6×DG×=6,∴DG=2.过点D作DP⊥CF,连接OD,∵AB⊥CF,DG⊥AB,∴四边形PDGE为矩形,∴PE=DG=2,∴CP=PE+CE=2+9=11.在Rt△OPD中,OP=5,OD=6,∴DP==,∴在Rt△CPD中,根据勾股定理得,CD==2
第27章 圆
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
A.点P在⊙O外 B.点P在⊙O上
C.点P在⊙O内 D.无法确定
2. 如图,在平面直角坐标系中,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为上一点(不与O,A两点重合),则cos C的值为( )
A. B. C. D.
3. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影=( )
A.π B.2π C.π D.π
4. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A.2 B.3 C.4 D.5
5. 如图,已知⊙O的直径AB⊥弦CD于点E.则下列结论中一定正确的是( )
A.AE=OE B.CE=DE C.OE=CE D.∠AOC=60°
6. 如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
A. B. C. D.
7. 如图,点A,B,C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,若∠DCE=40°,则∠ACB的度数为( )
A.140° B.70° C.110° D.80°
8. 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,到半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.3π B.4π C.5π D.6π
9.如图,圆内接正六边形的边长为4,以其各边为直径作半圆,则图中阴影部分的面积为( )
A.24-4π B.12+4π C.24+8π D.24+4π
10. 如图,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC,下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD:S△BOC=AD2:AO2;④OD:OC=DE:EC;⑤OD2=DE·CD.正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共6小题,4*6=24)
11. 如图,在⊙O中,=,∠A=30°,则∠B=__ __.
12. 如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D为⊙O上一点,若∠CAB=55°,则∠ADC的大小为__________度.
13. 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=110°.连接AC,则∠A的度数是________.
14. 如图, ⊙O的直径为20 cm,弦AB=16 cm,OD⊥AB,垂足为点D.则AB沿OD所在直线方向平移_________cm时可与⊙O相切.
15.如图,菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O按顺时针方向旋转90°,则图中阴影部分的面积是 _______________.
16.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10 mm.测得钢珠顶端离零件表面的距离为8 mm,如图所示,则这个小圆孔的宽口AB的长为_____mm.
三.解答题(共5小题, 56分)
17.(6分) 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面图;(要求尺规作图,保留作图痕迹,不写作法)
(2)若有水部分的水面宽AB=32 cm,水最深处的地方高度为8 cm,求这个圆形截面的半径.
18.(8分) 如图,圆O通过五边形OABCD的四个顶点.若∠AOD=150°,∠A=75°,∠D=60°,求证:BC=DC.
19.(8分) 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=10,BC=6,求CD的长.
20.(10分) 如图, A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连结CD,AD.
(1)求证:DB平分∠ADC;
(2)若BE=3,ED=6,求AB的长.
21.(12分) 如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连结OF.
(1)求证:OD∥BE;
(2)猜想:OF与CD有何数量关系?并说明理由.
22.(12分) 如图①,已知⊙O是△ADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
(1)求证:AC=BC;
(2)如图②,在图①的基础上作⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH∥BC,求∠ACF的度数;
(3)在(2)的条件下,若△ABD的面积为6,△ABD与△ABC的面积比为2∶9,求CD的长.
参考答案
1-5CADAB 6-10ACCAC
11.75°
12.35
13.35°
14.4或16
15.π-
16.8
17.解:(1)如图所示.
(2)连结OA,易知点D为AB的中点,∵AB=32 cm,∴AD=AB=16 cm,设这个圆形截面的半径为x cm,又∵CD=8 cm,∴OD=(x-8) cm,在Rt△OAD中,∵OD2+AD2=OA2,即(x-8)2+162=x2,解得x=20,∴圆形截面的半径为20 cm.
18. 证明:连结OB,OC.∵OA=OB=OC=OD,∴△OAB,△OBC,△OCD皆为等腰三角形.∵∠A=75°,∠D=60°,∴∠1=180°-2∠A=180°-2×75°=30°,∠2=180°-2∠D=180°-2×60°=60°.∵∠AOD=150°,∴∠3=∠AOD-∠1-∠2=150°-30°-60°=60°=∠2,∴BC=DC
19.(1)证明:连接AC,OC,如图,∵CD为切线,∴OC⊥CD,又∵CD⊥AD,∴OC∥AD,∴∠OCB=∠E,∵OB=OC,∴∠OCB=∠B,∴∠B=∠E,∴AE=AB
(2)解:∵AB为直径,∴∠ACB=90°,∴AC==8,∵AB=AE=10,AC⊥BE,∴CE=BC=6,∵CD·AE=AC·CE,∴CD==
20. 解:(1)∵AB=BC,∴=,∴∠ADB=∠BDC,∴DB平分∠ADC (2)由(1)可知,=,∴∠BAC=∠ADB,又∵∠ABE=∠ABD,∴△ABE∽△DBA,∴=,∵BE=3,ED=6,∴BD=9,∴AB2=BE·BD=3×9=27,∴AB=3
21.解:(1)连结OE,∵AM,DE是⊙O的切线,OA,OE是⊙O的半径,∴∠ADO=∠EDO,∠DAO=∠DEO=90°,∴∠AOD=∠EOD=∠AOE.∵∠ABE=∠AOE,∴∠AOD=∠ABE,∴OD∥BE
(2)OF=CD.理由如下:连结OC,∵BC,CE是⊙O的切线,OB,OE是⊙O半径,∴∠OBC=90°,∠OCB=∠OCE,同理:∠ADO=∠EDO.∵∠OAD+∠OBC=180°,∴AM∥BN,∴∠ADO+∠EDO+∠OCB+∠OCE=180°,∴∠EDO+∠OCE=90°,∴∠DOC=90°,在Rt△DOC中,∵F是DC的中点,∴OF=CD
22.解:(1)证明:∵DC平分∠ADB,∴∠ADC=∠BDC,∴=,∴AC=BC
(2)连接AO并延长交BC于点I,交⊙O于点J.∵AH是⊙O的切线,且AH∥BC,∴AI⊥BC.由垂径定理,得BI=IC,∴AI垂直平分BC,∴AB=AC=BC,∴△ABC是等边三角形,∠ABC=60°=∠F,∵FC是直径,∴∠FAC=90°,∴∠ACF=180°-90°-60°=30°
(3)过点D作DG⊥AB,∵△ABC为等边三角形,∠ACF=30°,∴AB⊥CF,∴AE=BE,∵S△ABC=AB2=27,∴AB=6,∴AE=3,CE=9,在Rt△AEO中,设EO=x,则AO=2x,∴AO2=AE2+OE2,∴(2x)2=(3)2+x2,∴x=3,∴⊙O的半径为6,∴CF=12,∵S△ABD=AB×DG×=6×DG×=6,∴DG=2.过点D作DP⊥CF,连接OD,∵AB⊥CF,DG⊥AB,∴四边形PDGE为矩形,∴PE=DG=2,∴CP=PE+CE=2+9=11.在Rt△OPD中,OP=5,OD=6,∴DP==,∴在Rt△CPD中,根据勾股定理得,CD==2
