鲁教版数学七年级下册7.2解二元一次方程组(1) 课件(共22张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册7.2解二元一次方程组(1) 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
2022年春鲁教版数学
七年级下册数学精品课件
7.2 解二元一次方程组
第1课时(代入消元法)
回顾与思考
1.什么叫二元一次方程?
2.什么叫二元一次方程组?
3.什么叫二元一次方程组的解?
学习目标
1.会用代入消元法解二元一次方程组
2.了解解二元一次方程组的消元思想,初步体现数学研究中“化未知为已知”的化归思想,从而变陌生为熟悉
重点:用代入消元法解二元一次方程组
昨天,我们8个人去红山公园玩,买门票花了34元.
每张成人票5元,每张儿童票3元.他们到底去了几个成人、几个儿童呢
还记得下面这一问题吗
设他们中有x个成人,y个儿童
我们列出的二元一次方程组为
我们怎么获得这个二元一次方程组的解呢
想想以前学习过的一元一次方程,能不能解决这一问题
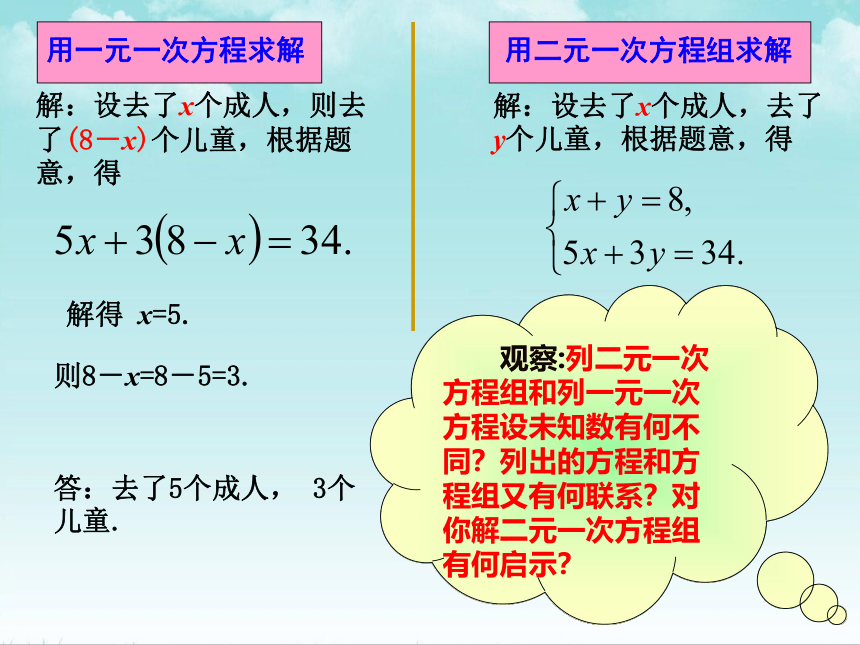
解:设去了x个成人,则去了(8-x)个儿童,根据题意,得
解得 x=5.
则8-x=8-5=3.
答:去了5个成人, 3个儿童.
用一元一次方程求解
用二元一次方程组求解
解:设去了x个成人,去了y个儿童,根据题意,得
观察:列二元一次方程组和列一元一次方程设未知数有何不同?列出的方程和方程组又有何联系?对你解二元一次方程组有何启示?
用二元一次方程组求解
由①,得y = 8-x. ③
将③代入②,得
5x+3(8-x)=34.
解得x = 5.
把x = 5代入③,得y = 3.
所以原方程组的解为
解:
练一练,上节课提出的问题:老牛和小马到底各驮了几个包裹呢?
这就需要解下面的方程组:
①
②
由①得,y=x-2. ③
由于方程组中相同的字母表示同一个未知数,所以方程②中的y也等于x-2,可以用x-2代替方程②中的y.这样有
x+1=2(x-2-1) ④
解所得的一元一次方程④,得x=7.
再把x=7代入③, 得y=5.
这样,我们就得到原方程组的解
因此老牛驮了7个包裹,小马驮了5个包裹.
x-y=2
x+1=2(y-1)
x=7 y=5
解:
想一想:
解二元一次方程组的基本思路是什么?
解二元一次方程组的基本思路是消元,把“二元”变为“一元”.
前面解方程组是将其中一个方程的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程.这种解方程组的方法称为代入消元法,简称代入法.
例1解方程组
3x+2y=14 ①x=y+3 ②
解:将②代入①,得3(y+3)+2y=14.
去括号,得3y+9+2y=14.
移项,合并同类项,得5y=5.
两边同时除以未知数的系数5,得y=1.
将y=1代入②,得x=4.
所以原方程组的解是
x=4 y=1
把所求的解代入原方程组,可以知道你解得对不对.
练习解下列方程组:
y=2x x+y=12
(1)
(2)
x=(y-5)÷24x+3y=65
相信自己,一定能行!
答案:
(1)
x=4 y=8
(2)
x=5 y=15
例2 解方程组:
2x+3y=16 ① x+4y=13 ②
解:由②,得 x=13-4y. ③
将③代入①,得2(13-4y)+3y=16.
去括号,得:26-8y+3y=16.
移项,合并同类项,得-5y=-10.
两边同时除以-5,得y=2.
将y=2代入③,得 x=5.
所以原方程组的解是
x=5 y=2
练习:用代入消元法解下列方程组
(1)
4x+3y=5 x-2y=4
(2)
3x-2y=9 x+2y=3
比一比 看谁算得又对又快!
答案:
(1)
x=2
y=-1
(2)
x=3 y=0
例3 解下列方程组:
解方程组的主要步骤有哪些?
思考
解二元一次方程组的步骤:
第1步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第2步:把此代数式代入没有变形的另一个方程中,可得一个一元一次方程.
第3步:解这个一元一次方程,得到一个未知数的值.
第4步:回代求出另一个未知数的值.
第5步:把方程组的解表示出来.
第6步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
小窍门
用代入消元法解下列方程组
(2)
5x+6y=13
7x+18y= 1
{
X=5
y= 2
(3)
x-y=5
2x+y=4
X=3
y=-2
{
{
{
(1)
{
X+2y=4
2x-y=3
{
X=2
y=1
通过本节课学习,你有什么收获?
1.本节课我们知道了用代入消元法解二元一次方程组的基本思路是“消元”.即 把“二元”化为“一元”,化二元一次方程组为一元一次方程.
2.把求出的解代入原方程组,可以检验解是否正确.
作业:课后习题
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
七年级下册数学精品课件
7.2 解二元一次方程组
第1课时(代入消元法)
回顾与思考
1.什么叫二元一次方程?
2.什么叫二元一次方程组?
3.什么叫二元一次方程组的解?
学习目标
1.会用代入消元法解二元一次方程组
2.了解解二元一次方程组的消元思想,初步体现数学研究中“化未知为已知”的化归思想,从而变陌生为熟悉
重点:用代入消元法解二元一次方程组
昨天,我们8个人去红山公园玩,买门票花了34元.
每张成人票5元,每张儿童票3元.他们到底去了几个成人、几个儿童呢
还记得下面这一问题吗
设他们中有x个成人,y个儿童
我们列出的二元一次方程组为
我们怎么获得这个二元一次方程组的解呢
想想以前学习过的一元一次方程,能不能解决这一问题
解:设去了x个成人,则去了(8-x)个儿童,根据题意,得
解得 x=5.
则8-x=8-5=3.
答:去了5个成人, 3个儿童.
用一元一次方程求解
用二元一次方程组求解
解:设去了x个成人,去了y个儿童,根据题意,得
观察:列二元一次方程组和列一元一次方程设未知数有何不同?列出的方程和方程组又有何联系?对你解二元一次方程组有何启示?
用二元一次方程组求解
由①,得y = 8-x. ③
将③代入②,得
5x+3(8-x)=34.
解得x = 5.
把x = 5代入③,得y = 3.
所以原方程组的解为
解:
练一练,上节课提出的问题:老牛和小马到底各驮了几个包裹呢?
这就需要解下面的方程组:
①
②
由①得,y=x-2. ③
由于方程组中相同的字母表示同一个未知数,所以方程②中的y也等于x-2,可以用x-2代替方程②中的y.这样有
x+1=2(x-2-1) ④
解所得的一元一次方程④,得x=7.
再把x=7代入③, 得y=5.
这样,我们就得到原方程组的解
因此老牛驮了7个包裹,小马驮了5个包裹.
x-y=2
x+1=2(y-1)
x=7 y=5
解:
想一想:
解二元一次方程组的基本思路是什么?
解二元一次方程组的基本思路是消元,把“二元”变为“一元”.
前面解方程组是将其中一个方程的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程.这种解方程组的方法称为代入消元法,简称代入法.
例1解方程组
3x+2y=14 ①x=y+3 ②
解:将②代入①,得3(y+3)+2y=14.
去括号,得3y+9+2y=14.
移项,合并同类项,得5y=5.
两边同时除以未知数的系数5,得y=1.
将y=1代入②,得x=4.
所以原方程组的解是
x=4 y=1
把所求的解代入原方程组,可以知道你解得对不对.
练习解下列方程组:
y=2x x+y=12
(1)
(2)
x=(y-5)÷24x+3y=65
相信自己,一定能行!
答案:
(1)
x=4 y=8
(2)
x=5 y=15
例2 解方程组:
2x+3y=16 ① x+4y=13 ②
解:由②,得 x=13-4y. ③
将③代入①,得2(13-4y)+3y=16.
去括号,得:26-8y+3y=16.
移项,合并同类项,得-5y=-10.
两边同时除以-5,得y=2.
将y=2代入③,得 x=5.
所以原方程组的解是
x=5 y=2
练习:用代入消元法解下列方程组
(1)
4x+3y=5 x-2y=4
(2)
3x-2y=9 x+2y=3
比一比 看谁算得又对又快!
答案:
(1)
x=2
y=-1
(2)
x=3 y=0
例3 解下列方程组:
解方程组的主要步骤有哪些?
思考
解二元一次方程组的步骤:
第1步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第2步:把此代数式代入没有变形的另一个方程中,可得一个一元一次方程.
第3步:解这个一元一次方程,得到一个未知数的值.
第4步:回代求出另一个未知数的值.
第5步:把方程组的解表示出来.
第6步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
小窍门
用代入消元法解下列方程组
(2)
5x+6y=13
7x+18y= 1
{
X=5
y= 2
(3)
x-y=5
2x+y=4
X=3
y=-2
{
{
{
(1)
{
X+2y=4
2x-y=3
{
X=2
y=1
通过本节课学习,你有什么收获?
1.本节课我们知道了用代入消元法解二元一次方程组的基本思路是“消元”.即 把“二元”化为“一元”,化二元一次方程组为一元一次方程.
2.把求出的解代入原方程组,可以检验解是否正确.
作业:课后习题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
