鲁教版数学七年级下册7.3 二元一次方程组的应用(3) 课件(共26张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册7.3 二元一次方程组的应用(3) 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 20:59:42 | ||
图片预览








文档简介
(共26张PPT)
2022年春鲁教版数学
七年级下册数学精品课件
7.3 二元一次方程组的应用(3)
——里程碑上的数
有一对父子,他们的年龄都是一个两位数,爸爸说:“我们俩的年龄之和是68岁哦.”儿子说:“若把你的年龄写在我的年龄的左边,得到一个四位数;再把你的年龄写在我的右边,同样得到一个四位数.”爸爸说:“前一个四位数比后一个四位数大2178.”那么他们俩的年龄各是多少
你会求他们俩的年龄吗?
里程碑上的数
1.用二元一次方程组解决“里程碑上的数”这一有趣的数字问题和行程问题;
2.归纳出用二元一次方程组解决实际问题的一般步骤;
3.体会二元一次方程组解决实际问题的工具性;
4.体会重要的数学思想——转化思想.
里程碑上的数
有两个两位数a和b ,如果将a放在b的左边,就得到一个四位数,那么这个四位数用代数式表示为 ;如果将a放在b的右边,将得到一个新的四位数,那么这个四位数用代数式可表示为 .
(1)一个两位数,个位数字是a,十位数字是b,则这个两位数用代数式表示为 ,若交换个位和十位上的数字,得到一个新的两位数用代数式表示为 .
(2)一个两位数,个位上的数为x,十位上的数为y,如果在它们之间添上一个0,就得到一个三位数,这个三位数用代数式可以表示为 .
10b+a
10a+b
100y+x
100a+b
100b+a
如果28=2×10+8,那么35= .
3×10+5
如果1839=18×100+39,那么1536= .
15×100+36
里程碑上的数
温故而知新
学法指导:经验、模仿、练习→学以致用(相信模仿的力量)
12:00
14:00
13:00
是一个两位数,它的两个数字之和为7.
十位数字与个位数字与12:00时所看到的正好互换了.
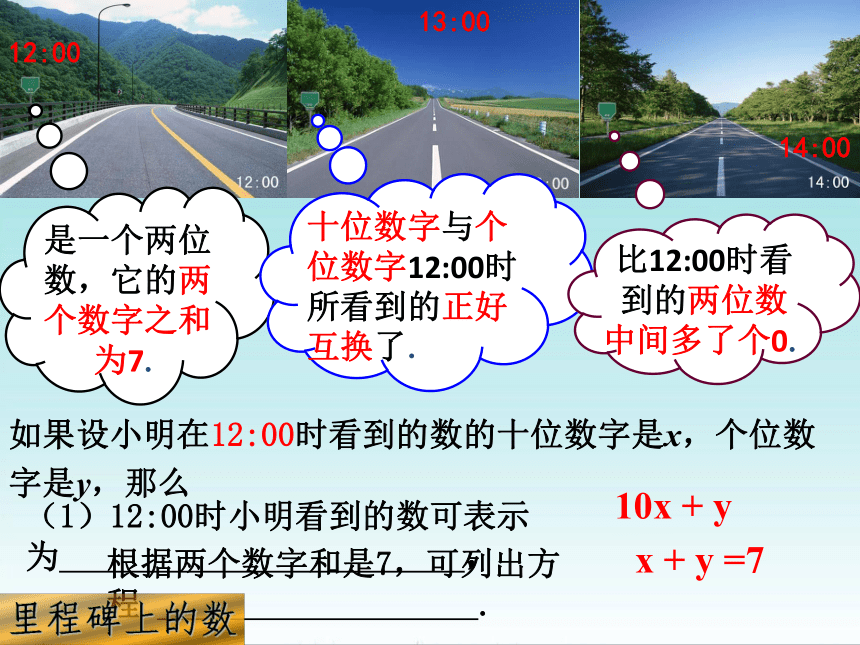
小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?
比12:00时看到的两位数中间多了个0.
里程碑上的数
12:00
14:00
13:00
(1)12:00时小明看到的数可表示为 ,
根据两个数字和是7,可列出方程 .
是一个两位数,它的两个数字之和为7.
十位数字与个位数字12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
10x + y
x + y =7
里程碑上的数
12:00
14:00
13:00
12:00~13:00间摩托车行驶的路程是:
(2)13:00时小明看到的数可表示为 ,
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
10y + x
(10y +x)- (10x +y)
是一个两位数,它的两个数字之和为7。
十位数字与个位数字12:00时所看到的正好互换了。
比12:00时看到的两位数中间多了个0。
里程碑上的数
12:00
14:00
13:00
(3)14:00是小明看到的数可表示为 ,
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
100x + y
(100x +y )- (10y +x )
13:00~14:00间摩托车行驶的路程是:
是一个两位数,它的两个数字之和为7。
十位数字与个位数字12:00时所看到的正好互换了。
比12:00时看到的两位数中间多了个0。
里程碑上的数
是一个两位数,它的两个数字之和为7.
十位与个位数字与12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
(4)12:00~13:00与13:00~14:00两段时间内摩托车的行驶路程有什么关系?你能列出相应的方程吗?
12:00
14:00
13:00
(3)14:00时小明看到的数可表示为 100x + y ,
13:00~14:00间摩托车行驶的路程是:(100x +y )- (10y +x ).
12:00~13:00间摩托车行驶的路程是(10y +x)- (10x +y).
(2)13:00时小明看到的数可表示为 10y + x ,
(1)12:00时小明看到的数可表示为10x + y ,
根据两个数字和是7,可列出方程x + y = 7.
里程碑上的数
是一个两位数,它的两个数字之和为7.
十位与个位数字与12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
解:如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
解得
答:小明在12:00时看到的里程碑上的数是16.
里程碑上的数
12:00是一个两位数,它的两个数字之和为7;
13:00十位与个位数字与12:00所看到的正好互换了;
14:00比12:00时看到的两位数中间多了个0.
分析:设小明在12:00看到的十位数字是x,个位数字是y,那么
时刻 百位数字 十位数字 个位数字 表达式
12:00
13:00
14:00
x
y
10 x + y
y
x
10 y + x
x
0
y
100 x + y
经验解题
里程碑上的数
相等关系:①12:00看到的数,两个数字之和是7
②路程差相等
学法小结:对较复杂的问题可以通过列表格的方法疏理题中的未知量,已知量以及等量关系,使其条理清楚,将复杂问题转化为简单问题.
解:如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
解得
答:小明在12:00时看到的里程碑上的数是16.
里程碑上的数
再看导入的问题
解:设爸爸的年龄为x,儿子的年龄为y,依题意得:
有一对父子,他们的年龄都是一个两位数,爸爸说:“我们俩的年龄之和是68岁哦.”儿子说:“若把你的年龄写在我的年龄的左边,得到一个四位数;若把你的年龄写在我的右边,同样得到一个四位数.”爸爸说:“前一个四位数比后一个四位数大2178.”那么他们俩的年龄各是多少
答:爸爸的年龄为45,儿子的年龄为23.
里程碑上的数
x + y = 68
(100x + y) -(100y + x) = 2178
{
1.审:审清题意(已知什么,求什么 已,未知之间有什么关系 审清题目中的等量关系)
2.设:设未知数(弄清设直接未知数还是间接未知数,语句要完整,有单位的要注明单位)
3.列:列代数式,根据等量关系列方程组;
4.解:解所列的方程组;
5.检:是否是所列方程组的解,是否符合题意;
6.答:答案也必需是完事的语句,注明单位且要与实际生活相符合.
列方程组解应用题的一般步骤是:
列方程组解应用题的关键是:
审、
设、
列、
解、
检、
答。
审清题目中的等量关系.
里程碑上的数
1.两个两位数的和是51,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数。已知前一个四位数比后一个四位数大2673,求这两个两位数.
答:较大的数为39 ,较小的数为12.
里程碑上的数
跟踪练习
x + y = 51
(100x + y) -(100y + x) = 2673
{
解:设较大的数为x,较小的数为y,依题意得:
解得
y=12
x=39
{
x + y = 51
x - y = 27
化简,得
{
跟踪练习
2.李刚骑摩托车在公路上匀速行驶,早晨7:00时看到里程碑上的数是一个两位数,它的数字之和是9;8:00时看里程碑上的两位数与7:00时看到的个位数和十位数互换了;9:00时看到里程碑上的数是7:00时看到的数的8倍,李刚在7:00时看到的数字是多少
里程碑上的数
时刻 十 个 表达式
7:00
8:00
9:00 8倍的“数”
3.一个两位数的十位数字与个位数字的和为7,如果将十位数与个位数字对调后,所得的数比原数小27,求原来的两位数.
解:设原来两位数的十位数字为x,个位数字为y,根据题意,得
解之得:
答:原来的两位数为52.
分析:
个位
十位
原数
新数
表达式
x
y
10x+y
10y+x
y
x
里程碑上的数
4.甲、乙两人相距42km,如果两人从两地相向而行,2小时后相遇,如果二人同时从两地出发,同向而行,14小时后甲追上乙,求二人的速度.
解:设甲的速度为x,乙的速度为y,则
化简,得
解得
所以甲的速度为12km/h,乙的速度为9km/h.
甲
乙
甲
乙
甲
乙
甲
乙
2x
2y
14x
14y
甲
乙
表达式
同向
异向
2x
2y
2x+2y=42
14y
42
14x
14y+42= 14x
里程碑上的数
2x+2y=42
14y+42=14x
x=12
y=9
x+y=21
x-y=3
1.小亮和小明做加法游戏, 小明在第一个加数的后面多写一个0, 所得和是242; 小亮在另一个加数的后面多写一个0, 所得和是341,求原来的两个加数分别是多少
解:设第一个加数为x,第二个加数为y, 根据题意得:
=
=
+
+
341
242
10
10y
x
y
x
=
=
32
21
y
x
当堂检测
里程碑上的数
解:设的甲速度为x千米/小时,乙的速度为y千米/小时,根据题意得:
2.A,B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度.
里程碑上的数
当堂检测
3.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
解:设十位上数字是x,个位上的数字是y,依题意得
x=5
y=6
里程碑上的数
当堂检测
勤于总结
1.审:审清题意:已知什么,求什么 已,未知之间有什么关系 审清题目中的等量关系;
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,根据等量关系列方程组;
4.解:解所列的方程;
5.检:是否是所列方程解;是否符合题意;
6.答:答案也必需是完事的语句,注明单位且要贴近生活.
列方程解应用题的一般步骤是:
列方程解应用题的关键是:审清题目中的等量关系。
审、设、列、解、检、答。
里程碑上的数
学法小结:对较复杂的问题可以通过列表格、画线段等方法疏理题中的未知量,已知量以及等量关系,使其条理清楚,将复杂问题转化为简单问题.
作业布置
1.课后习题
2.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
3.A,B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?
里程碑上的数
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
七年级下册数学精品课件
7.3 二元一次方程组的应用(3)
——里程碑上的数
有一对父子,他们的年龄都是一个两位数,爸爸说:“我们俩的年龄之和是68岁哦.”儿子说:“若把你的年龄写在我的年龄的左边,得到一个四位数;再把你的年龄写在我的右边,同样得到一个四位数.”爸爸说:“前一个四位数比后一个四位数大2178.”那么他们俩的年龄各是多少
你会求他们俩的年龄吗?
里程碑上的数
1.用二元一次方程组解决“里程碑上的数”这一有趣的数字问题和行程问题;
2.归纳出用二元一次方程组解决实际问题的一般步骤;
3.体会二元一次方程组解决实际问题的工具性;
4.体会重要的数学思想——转化思想.
里程碑上的数
有两个两位数a和b ,如果将a放在b的左边,就得到一个四位数,那么这个四位数用代数式表示为 ;如果将a放在b的右边,将得到一个新的四位数,那么这个四位数用代数式可表示为 .
(1)一个两位数,个位数字是a,十位数字是b,则这个两位数用代数式表示为 ,若交换个位和十位上的数字,得到一个新的两位数用代数式表示为 .
(2)一个两位数,个位上的数为x,十位上的数为y,如果在它们之间添上一个0,就得到一个三位数,这个三位数用代数式可以表示为 .
10b+a
10a+b
100y+x
100a+b
100b+a
如果28=2×10+8,那么35= .
3×10+5
如果1839=18×100+39,那么1536= .
15×100+36
里程碑上的数
温故而知新
学法指导:经验、模仿、练习→学以致用(相信模仿的力量)
12:00
14:00
13:00
是一个两位数,它的两个数字之和为7.
十位数字与个位数字与12:00时所看到的正好互换了.
小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?
比12:00时看到的两位数中间多了个0.
里程碑上的数
12:00
14:00
13:00
(1)12:00时小明看到的数可表示为 ,
根据两个数字和是7,可列出方程 .
是一个两位数,它的两个数字之和为7.
十位数字与个位数字12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
10x + y
x + y =7
里程碑上的数
12:00
14:00
13:00
12:00~13:00间摩托车行驶的路程是:
(2)13:00时小明看到的数可表示为 ,
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
10y + x
(10y +x)- (10x +y)
是一个两位数,它的两个数字之和为7。
十位数字与个位数字12:00时所看到的正好互换了。
比12:00时看到的两位数中间多了个0。
里程碑上的数
12:00
14:00
13:00
(3)14:00是小明看到的数可表示为 ,
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
100x + y
(100x +y )- (10y +x )
13:00~14:00间摩托车行驶的路程是:
是一个两位数,它的两个数字之和为7。
十位数字与个位数字12:00时所看到的正好互换了。
比12:00时看到的两位数中间多了个0。
里程碑上的数
是一个两位数,它的两个数字之和为7.
十位与个位数字与12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么
(4)12:00~13:00与13:00~14:00两段时间内摩托车的行驶路程有什么关系?你能列出相应的方程吗?
12:00
14:00
13:00
(3)14:00时小明看到的数可表示为 100x + y ,
13:00~14:00间摩托车行驶的路程是:(100x +y )- (10y +x ).
12:00~13:00间摩托车行驶的路程是(10y +x)- (10x +y).
(2)13:00时小明看到的数可表示为 10y + x ,
(1)12:00时小明看到的数可表示为10x + y ,
根据两个数字和是7,可列出方程x + y = 7.
里程碑上的数
是一个两位数,它的两个数字之和为7.
十位与个位数字与12:00时所看到的正好互换了.
比12:00时看到的两位数中间多了个0.
解:如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
解得
答:小明在12:00时看到的里程碑上的数是16.
里程碑上的数
12:00是一个两位数,它的两个数字之和为7;
13:00十位与个位数字与12:00所看到的正好互换了;
14:00比12:00时看到的两位数中间多了个0.
分析:设小明在12:00看到的十位数字是x,个位数字是y,那么
时刻 百位数字 十位数字 个位数字 表达式
12:00
13:00
14:00
x
y
10 x + y
y
x
10 y + x
x
0
y
100 x + y
经验解题
里程碑上的数
相等关系:①12:00看到的数,两个数字之和是7
②路程差相等
学法小结:对较复杂的问题可以通过列表格的方法疏理题中的未知量,已知量以及等量关系,使其条理清楚,将复杂问题转化为简单问题.
解:如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
解得
答:小明在12:00时看到的里程碑上的数是16.
里程碑上的数
再看导入的问题
解:设爸爸的年龄为x,儿子的年龄为y,依题意得:
有一对父子,他们的年龄都是一个两位数,爸爸说:“我们俩的年龄之和是68岁哦.”儿子说:“若把你的年龄写在我的年龄的左边,得到一个四位数;若把你的年龄写在我的右边,同样得到一个四位数.”爸爸说:“前一个四位数比后一个四位数大2178.”那么他们俩的年龄各是多少
答:爸爸的年龄为45,儿子的年龄为23.
里程碑上的数
x + y = 68
(100x + y) -(100y + x) = 2178
{
1.审:审清题意(已知什么,求什么 已,未知之间有什么关系 审清题目中的等量关系)
2.设:设未知数(弄清设直接未知数还是间接未知数,语句要完整,有单位的要注明单位)
3.列:列代数式,根据等量关系列方程组;
4.解:解所列的方程组;
5.检:是否是所列方程组的解,是否符合题意;
6.答:答案也必需是完事的语句,注明单位且要与实际生活相符合.
列方程组解应用题的一般步骤是:
列方程组解应用题的关键是:
审、
设、
列、
解、
检、
答。
审清题目中的等量关系.
里程碑上的数
1.两个两位数的和是51,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数。已知前一个四位数比后一个四位数大2673,求这两个两位数.
答:较大的数为39 ,较小的数为12.
里程碑上的数
跟踪练习
x + y = 51
(100x + y) -(100y + x) = 2673
{
解:设较大的数为x,较小的数为y,依题意得:
解得
y=12
x=39
{
x + y = 51
x - y = 27
化简,得
{
跟踪练习
2.李刚骑摩托车在公路上匀速行驶,早晨7:00时看到里程碑上的数是一个两位数,它的数字之和是9;8:00时看里程碑上的两位数与7:00时看到的个位数和十位数互换了;9:00时看到里程碑上的数是7:00时看到的数的8倍,李刚在7:00时看到的数字是多少
里程碑上的数
时刻 十 个 表达式
7:00
8:00
9:00 8倍的“数”
3.一个两位数的十位数字与个位数字的和为7,如果将十位数与个位数字对调后,所得的数比原数小27,求原来的两位数.
解:设原来两位数的十位数字为x,个位数字为y,根据题意,得
解之得:
答:原来的两位数为52.
分析:
个位
十位
原数
新数
表达式
x
y
10x+y
10y+x
y
x
里程碑上的数
4.甲、乙两人相距42km,如果两人从两地相向而行,2小时后相遇,如果二人同时从两地出发,同向而行,14小时后甲追上乙,求二人的速度.
解:设甲的速度为x,乙的速度为y,则
化简,得
解得
所以甲的速度为12km/h,乙的速度为9km/h.
甲
乙
甲
乙
甲
乙
甲
乙
2x
2y
14x
14y
甲
乙
表达式
同向
异向
2x
2y
2x+2y=42
14y
42
14x
14y+42= 14x
里程碑上的数
2x+2y=42
14y+42=14x
x=12
y=9
x+y=21
x-y=3
1.小亮和小明做加法游戏, 小明在第一个加数的后面多写一个0, 所得和是242; 小亮在另一个加数的后面多写一个0, 所得和是341,求原来的两个加数分别是多少
解:设第一个加数为x,第二个加数为y, 根据题意得:
=
=
+
+
341
242
10
10y
x
y
x
=
=
32
21
y
x
当堂检测
里程碑上的数
解:设的甲速度为x千米/小时,乙的速度为y千米/小时,根据题意得:
2.A,B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度.
里程碑上的数
当堂检测
3.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
解:设十位上数字是x,个位上的数字是y,依题意得
x=5
y=6
里程碑上的数
当堂检测
勤于总结
1.审:审清题意:已知什么,求什么 已,未知之间有什么关系 审清题目中的等量关系;
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,根据等量关系列方程组;
4.解:解所列的方程;
5.检:是否是所列方程解;是否符合题意;
6.答:答案也必需是完事的语句,注明单位且要贴近生活.
列方程解应用题的一般步骤是:
列方程解应用题的关键是:审清题目中的等量关系。
审、设、列、解、检、答。
里程碑上的数
学法小结:对较复杂的问题可以通过列表格、画线段等方法疏理题中的未知量,已知量以及等量关系,使其条理清楚,将复杂问题转化为简单问题.
作业布置
1.课后习题
2.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
3.A,B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?
里程碑上的数
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
