鲁教版数学七年级下册7.4二元一次方程与一次函数(1) 课件(共19张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册7.4二元一次方程与一次函数(1) 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
2022年春鲁教版数学
七年级下册数学精品课件
7.4 二元一次方程与一次函数(1)
十七世纪法国数学家笛卡尔有一次生病卧床,他看见屋顶上的一只蜘蛛顺着左右爬行,笛卡尔看到蜘蛛的“表演”猛的灵机一动.他想,可以把蜘蛛看成一个点,它可以上、下、左、右运动,能不能知道蜘蛛的位置用一组数确定下来呢?
在蜘蛛爬行的启示下,笛卡尔创建了直角坐标系,在坐标系下几何图形(形)和方程(数)建立联系.笛卡尔坐标系起到了桥梁和纽带的而我们可以把图形化成方程来研究,也可以用图象来研究方程.
这节课人们就来研究二元一次方程(数)与一次函数(形)的关系.
一次函数
这是怎么回事?
二元一次方程
你知道y=x+1是什么吗?
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
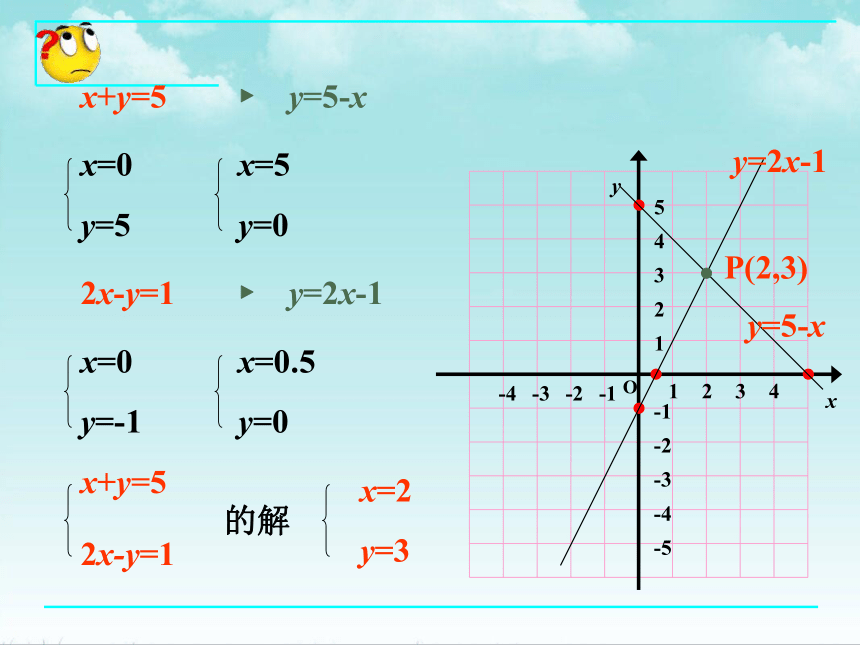
x+y=5
y=5-x
x=0
y=5
2x-y=1
x=0
y=-1
x=5
y=0
x=0.5
y=0
y=2x-1
y=2x-1
y=5-x
P(2,3)
x+y=5
2x-y=1
x=2
y=3
的解
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
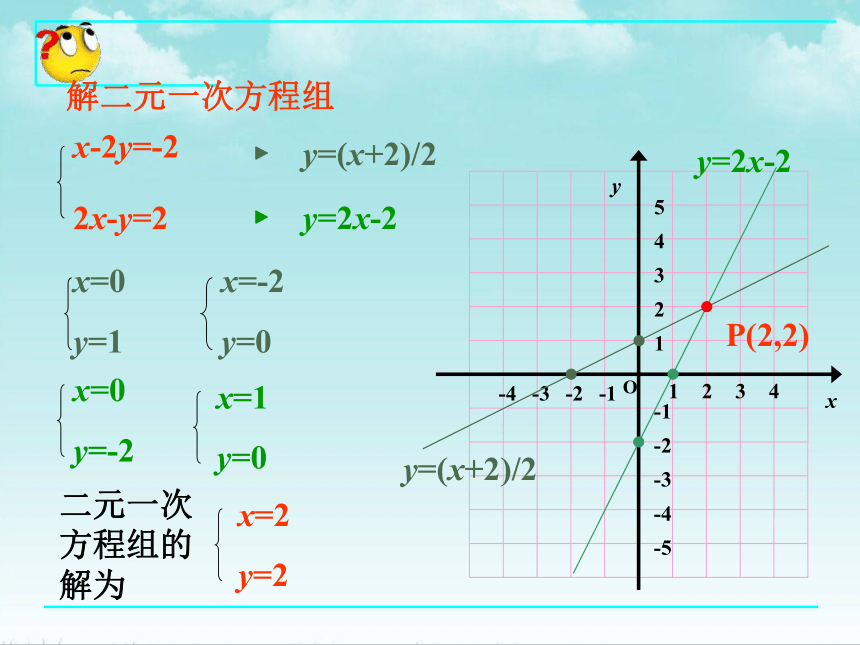
y=(x+2)/2
y=2x-2
x-2y=-2
2x-y=2
x=0
y=1
x=-2
y=0
x=0
y=-2
x=1
y=0
P(2,2)
解二元一次方程组
y=(x+2)/2
y=2x-2
x=2
y=2
二元一次方程组的解为
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
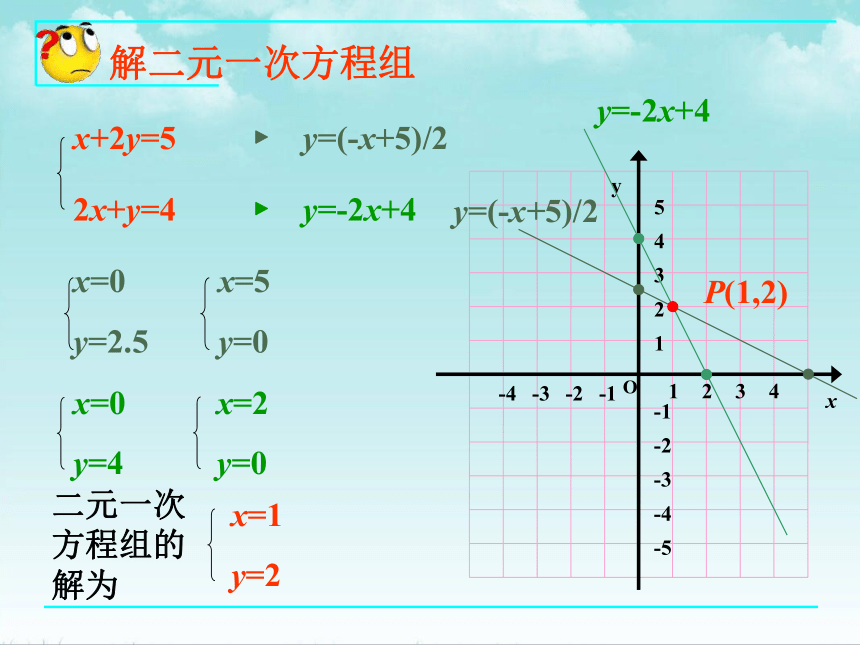
y=(-x+5)/2
y=-2x+4
x+2y=5
2x+y=4
x=0
y=2.5
x=5
y=0
x=0
y=4
x=2
y=0
P(1,2)
解二元一次方程组
y=-2x+4
y=(-x+5)/2
x=1
y=2
二元一次方程组的解为
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
练习
P(3,-2)
6
5
2x+y=4
2x-3y=12
x=3
y=-2
二元一次方程组的解为
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
练习
6
5
y=2-x
y=5-x
无解
(1)函数y=x+1上的任意一点的坐标是否满足方程x-y=-1?
(2)以方程x-y=-1的解为坐标的点在不在函数y=x+1的图象上?
(3)方程x-y=-1与函数y=x+1有何关系?
以方程x-y=-1的解为坐标的点组成的图象与一次函数y=x+1的图象相同.
在同一坐标系下画出y=x+1与y=4x-2的图象,他们的交点坐标是什么?
结论:函数y=x+1和y=4x-2的交点坐标就是有两个函数表达式组成的方程组 的解.
方程组
的解是什么?
用方程的方法可以解决图象的问题.
用图象法可以解决图象问题
噢!函数和方程有联系.
解方程组
解:由
可得
在同一直角坐标系内作出一次函数 的图象l1和 的图象l2, 如图所示
同理,由 可得
所以方程 的解是
得l1,l2的交点为P(2,2).
方程与函数关系的应用
1.把两个方程都 画成函数表达式的形式.
2.画出两个函数的图象.
3.画出交点坐标,交点坐标即为方程组的解.
方程组 解的情况如何?
你能从函数角度解释一下吗?
本节课我们通过操作和思考,揭示了二元一次方程和函数图象之间的对应关系,从而引入二元一次方程组的图象解法,同时也建立了“数”——二元一次方程与“形”——函数图象之间的对应关系,培养了学生初步的数形结合的意识和能力.
课后习题
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
七年级下册数学精品课件
7.4 二元一次方程与一次函数(1)
十七世纪法国数学家笛卡尔有一次生病卧床,他看见屋顶上的一只蜘蛛顺着左右爬行,笛卡尔看到蜘蛛的“表演”猛的灵机一动.他想,可以把蜘蛛看成一个点,它可以上、下、左、右运动,能不能知道蜘蛛的位置用一组数确定下来呢?
在蜘蛛爬行的启示下,笛卡尔创建了直角坐标系,在坐标系下几何图形(形)和方程(数)建立联系.笛卡尔坐标系起到了桥梁和纽带的而我们可以把图形化成方程来研究,也可以用图象来研究方程.
这节课人们就来研究二元一次方程(数)与一次函数(形)的关系.
一次函数
这是怎么回事?
二元一次方程
你知道y=x+1是什么吗?
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
x+y=5
y=5-x
x=0
y=5
2x-y=1
x=0
y=-1
x=5
y=0
x=0.5
y=0
y=2x-1
y=2x-1
y=5-x
P(2,3)
x+y=5
2x-y=1
x=2
y=3
的解
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=(x+2)/2
y=2x-2
x-2y=-2
2x-y=2
x=0
y=1
x=-2
y=0
x=0
y=-2
x=1
y=0
P(2,2)
解二元一次方程组
y=(x+2)/2
y=2x-2
x=2
y=2
二元一次方程组的解为
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=(-x+5)/2
y=-2x+4
x+2y=5
2x+y=4
x=0
y=2.5
x=5
y=0
x=0
y=4
x=2
y=0
P(1,2)
解二元一次方程组
y=-2x+4
y=(-x+5)/2
x=1
y=2
二元一次方程组的解为
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
练习
P(3,-2)
6
5
2x+y=4
2x-3y=12
x=3
y=-2
二元一次方程组的解为
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
练习
6
5
y=2-x
y=5-x
无解
(1)函数y=x+1上的任意一点的坐标是否满足方程x-y=-1?
(2)以方程x-y=-1的解为坐标的点在不在函数y=x+1的图象上?
(3)方程x-y=-1与函数y=x+1有何关系?
以方程x-y=-1的解为坐标的点组成的图象与一次函数y=x+1的图象相同.
在同一坐标系下画出y=x+1与y=4x-2的图象,他们的交点坐标是什么?
结论:函数y=x+1和y=4x-2的交点坐标就是有两个函数表达式组成的方程组 的解.
方程组
的解是什么?
用方程的方法可以解决图象的问题.
用图象法可以解决图象问题
噢!函数和方程有联系.
解方程组
解:由
可得
在同一直角坐标系内作出一次函数 的图象l1和 的图象l2, 如图所示
同理,由 可得
所以方程 的解是
得l1,l2的交点为P(2,2).
方程与函数关系的应用
1.把两个方程都 画成函数表达式的形式.
2.画出两个函数的图象.
3.画出交点坐标,交点坐标即为方程组的解.
方程组 解的情况如何?
你能从函数角度解释一下吗?
本节课我们通过操作和思考,揭示了二元一次方程和函数图象之间的对应关系,从而引入二元一次方程组的图象解法,同时也建立了“数”——二元一次方程与“形”——函数图象之间的对应关系,培养了学生初步的数形结合的意识和能力.
课后习题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
