广平中学2012——2013第一学期第二次数学竞赛试题
文档属性
| 名称 | 广平中学2012——2013第一学期第二次数学竞赛试题 |  | |
| 格式 | zip | ||
| 文件大小 | 61.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-01 17:04:43 | ||
图片预览

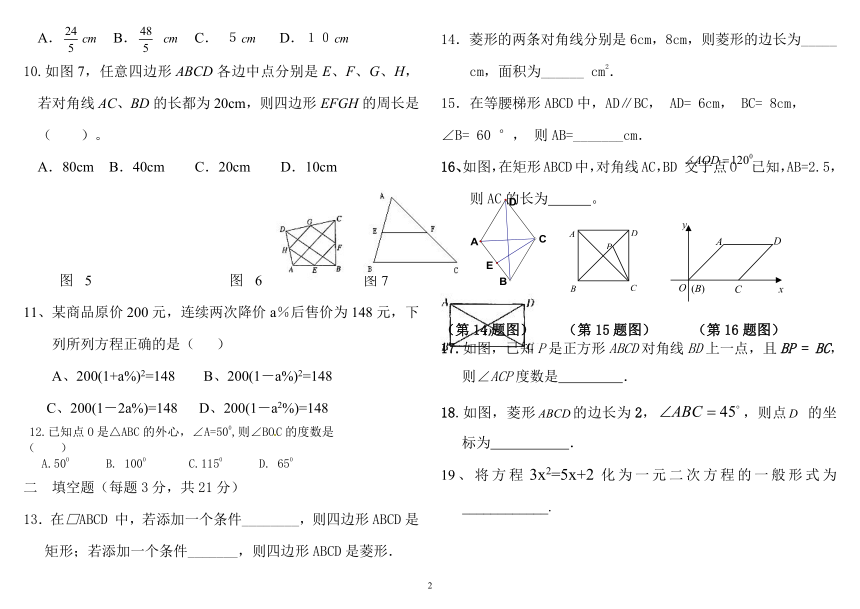
文档简介
广平中学2012——2013第一学期第二次竞赛试题
一选择题(细心选一选 每题3分,共36分)
1.如图1,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm C.9 cm D.12 cm
2.等腰三角形的底和腰是方程的两个根,则这个三角形的周长是( )
A.8 B.10 C.8或10 D. 不能确定
3.如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则AC的度数是( )
A. 30° B. 60° C. 90° D. 120°
4.、用配方法解方程,下列配方正确的是 ( )
A. B.
C. D.
5.如图2,将矩形ABCD沿对角线BD对折,使点C落在C′处,BC′交AD于F,下列不成立的是( )。
A.AF=C′F B.BF=DF
C.∠BDA=∠ADC′ D.∠ABC′=∠ADC′
6.如图3,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF.则∠CDF等于( )。
A.80° B.70° C.65° D.60°
7.如图4,梯形ABCD中,对角线AC与BD交于点O,则图中面积相等的三角形有( )。
A.1对 B.2对 C.3对 D. 4对
图1 图2 图3 图4
8.如图5,EF是△ABC的中位线,若AE=4,AF=5,BC=12,则△AEF的周长是( )
(A)7.5 (B)30 (C)15 (D)24
9.如图6,在菱形ABCD中,,则菱形AB边上的高CE的长是( )。
A. B. C. 5 D.10
10.如图7,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是( )。
A.80cm B.40cm C.20cm D.10cm
图5 图6 图7
11、某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A、200(1+a%)2=148 B、200(1-a%)2=148
C、200(1-2a%)=148 D、200(1-a2%)=148
12.已知点O是△ABC的外心,∠A=500,则∠BOC的度数是 ( )
A.500 B. 1000 C.1150 D. 650
二 填空题(每题3分,共21分)
13.在□ABCD 中,若添加一个条件________,则四边形ABCD是矩形;若添加一个条件_______,则四边形ABCD是菱形.
14.菱形的两条对角线分别是6cm,8cm,则菱形的边长为_____ cm,面积为______ cm2.
15.在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=8cm,
∠B=60°,则AB=_______cm.
16、如图,在矩形ABCD中,对角线AC,BD 交于点O 已知,AB=2.5,则AC的长为 。
(第14题图) (第15题图) (第16题图)
17.如图,已知P是正方形ABCD对角线BD上一点,且BP = BC,则∠ACP度数是 .
18.如图,菱形的边长为2,,则点 的坐标为 .
19、将方程3x2=5x+2化为一元二次方程的一般形式为____________.
答案卷
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
二、填空题
13﹍﹍﹍﹍﹍、﹍﹍﹍﹍﹍﹍14﹍﹍﹍﹍、﹍﹍﹍﹍﹍15﹍﹍﹍
16﹍﹍﹍17﹍﹍﹍18﹍﹍﹍19﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍
三问答题 20、解方程(8分)
.
21.(9分)如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB于E, DF∥AB交AC于F,求证:DE+DF=AC
22.(9分) 已知:如图, □ABCD各角的平分线分别相交于点E,F,G,H,
求证:四边形EFGH是矩形.
23、(9分)如图,AB是⊙O的直径,CD是⊙O的弦,AB=6, ∠DCB=30°,求弦BD的长。
24.(本题满分9分)在梯形ABCD中,AB∥CD,∠A=90°, AB=2,BC=3,CD=1,E是AD中点. 求证:CE⊥BE.
25.(9分)在直径为650mm的圆柱形油罐内装进一些油后,其横截面如图,若油面宽AB=600mm,求油的最大深度。
26、(10分)已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
一选择题(细心选一选 每题3分,共36分)
1.如图1,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm C.9 cm D.12 cm
2.等腰三角形的底和腰是方程的两个根,则这个三角形的周长是( )
A.8 B.10 C.8或10 D. 不能确定
3.如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则AC的度数是( )
A. 30° B. 60° C. 90° D. 120°
4.、用配方法解方程,下列配方正确的是 ( )
A. B.
C. D.
5.如图2,将矩形ABCD沿对角线BD对折,使点C落在C′处,BC′交AD于F,下列不成立的是( )。
A.AF=C′F B.BF=DF
C.∠BDA=∠ADC′ D.∠ABC′=∠ADC′
6.如图3,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF.则∠CDF等于( )。
A.80° B.70° C.65° D.60°
7.如图4,梯形ABCD中,对角线AC与BD交于点O,则图中面积相等的三角形有( )。
A.1对 B.2对 C.3对 D. 4对
图1 图2 图3 图4
8.如图5,EF是△ABC的中位线,若AE=4,AF=5,BC=12,则△AEF的周长是( )
(A)7.5 (B)30 (C)15 (D)24
9.如图6,在菱形ABCD中,,则菱形AB边上的高CE的长是( )。
A. B. C. 5 D.10
10.如图7,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是( )。
A.80cm B.40cm C.20cm D.10cm
图5 图6 图7
11、某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A、200(1+a%)2=148 B、200(1-a%)2=148
C、200(1-2a%)=148 D、200(1-a2%)=148
12.已知点O是△ABC的外心,∠A=500,则∠BOC的度数是 ( )
A.500 B. 1000 C.1150 D. 650
二 填空题(每题3分,共21分)
13.在□ABCD 中,若添加一个条件________,则四边形ABCD是矩形;若添加一个条件_______,则四边形ABCD是菱形.
14.菱形的两条对角线分别是6cm,8cm,则菱形的边长为_____ cm,面积为______ cm2.
15.在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=8cm,
∠B=60°,则AB=_______cm.
16、如图,在矩形ABCD中,对角线AC,BD 交于点O 已知,AB=2.5,则AC的长为 。
(第14题图) (第15题图) (第16题图)
17.如图,已知P是正方形ABCD对角线BD上一点,且BP = BC,则∠ACP度数是 .
18.如图,菱形的边长为2,,则点 的坐标为 .
19、将方程3x2=5x+2化为一元二次方程的一般形式为____________.
答案卷
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
二、填空题
13﹍﹍﹍﹍﹍、﹍﹍﹍﹍﹍﹍14﹍﹍﹍﹍、﹍﹍﹍﹍﹍15﹍﹍﹍
16﹍﹍﹍17﹍﹍﹍18﹍﹍﹍19﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍
三问答题 20、解方程(8分)
.
21.(9分)如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB于E, DF∥AB交AC于F,求证:DE+DF=AC
22.(9分) 已知:如图, □ABCD各角的平分线分别相交于点E,F,G,H,
求证:四边形EFGH是矩形.
23、(9分)如图,AB是⊙O的直径,CD是⊙O的弦,AB=6, ∠DCB=30°,求弦BD的长。
24.(本题满分9分)在梯形ABCD中,AB∥CD,∠A=90°, AB=2,BC=3,CD=1,E是AD中点. 求证:CE⊥BE.
25.(9分)在直径为650mm的圆柱形油罐内装进一些油后,其横截面如图,若油面宽AB=600mm,求油的最大深度。
26、(10分)已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
同课章节目录
