1.1空间几何体的结构同步课时作业-2021-2022学年高一下学期数学人教A版必修2 (word含解析)
文档属性
| 名称 | 1.1空间几何体的结构同步课时作业-2021-2022学年高一下学期数学人教A版必修2 (word含解析) | 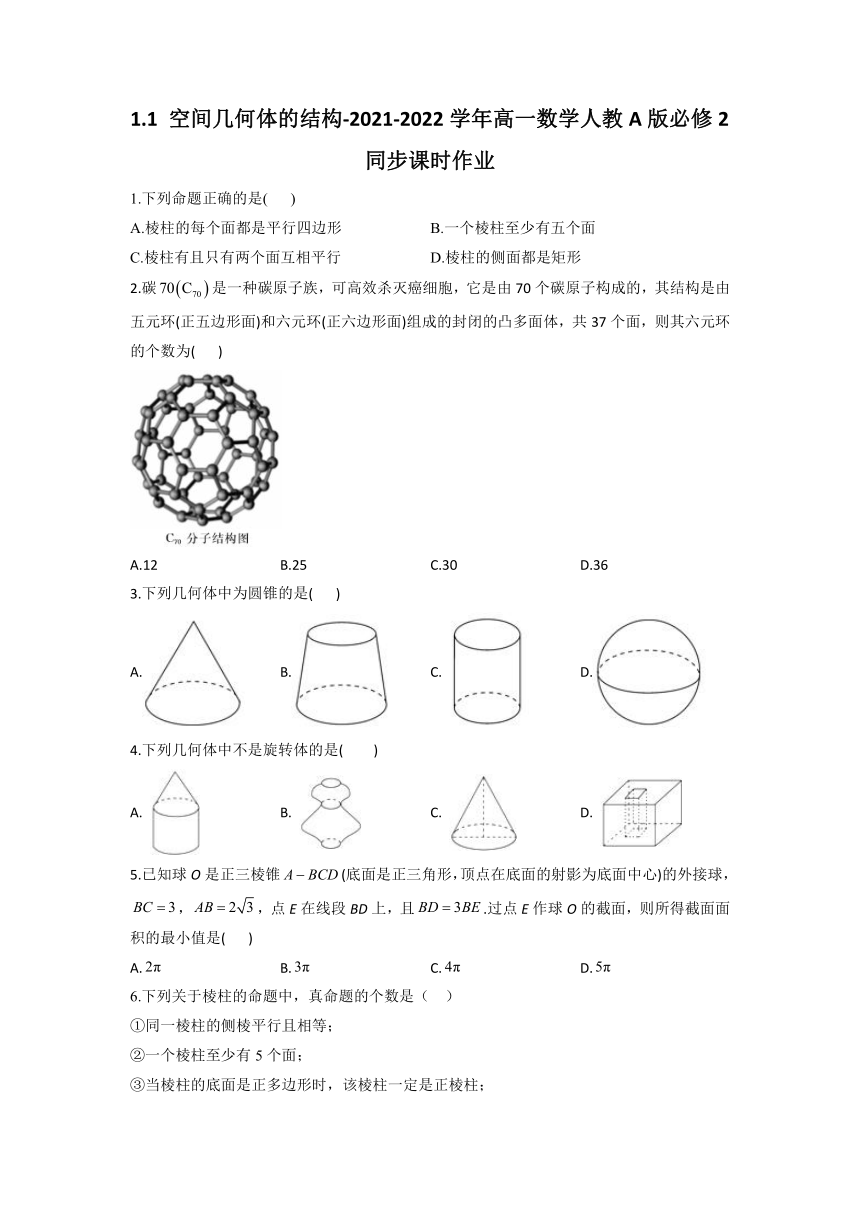 | |
| 格式 | zip | ||
| 文件大小 | 213.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 08:23:23 | ||
图片预览



文档简介
1.1 空间几何体的结构-2021-2022学年高一数学人教A版必修2同步课时作业
1.下列命题正确的是( )
A.棱柱的每个面都是平行四边形 B.一个棱柱至少有五个面
C.棱柱有且只有两个面互相平行 D.棱柱的侧面都是矩形
2.碳是一种碳原子族,可高效杀灭癌细胞,它是由70个碳原子构成的,其结构是由五元环(正五边形面)和六元环(正六边形面)组成的封闭的凸多面体,共37个面,则其六元环的个数为( )
A.12 B.25 C.30 D.36
3.下列几何体中为圆锥的是( )
A. B. C. D.
4.下列几何体中不是旋转体的是( )
A. B. C. D.
5.已知球O是正三棱锥(底面是正三角形,顶点在底面的射影为底面中心)的外接球,,,点E在线段BD上,且.过点E作球O的截面,则所得截面面积的最小值是( )
A. B. C. D.
6.下列关于棱柱的命题中,真命题的个数是( )
①同一棱柱的侧棱平行且相等;
②一个棱柱至少有5个面;
③当棱柱的底面是正多边形时,该棱柱一定是正棱柱;
④当棱柱的底面是等腰梯形时,该棱柱一定是平行六面体.
A.1 B.2 C.3 D.4
7.给出下列说法:
①任何一个几何体都必须有顶点、棱和面;
②一个几何体可以没有顶点;
③一个几何体可以没有棱;
④一个几何体可以没有面.
其中正确的个数是( )
A.1 B.2 C.3 D.4
8.在我国古代数学名著中有这样一个问题:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周长为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺?”这个问题中,葛藤长的最小值为(注:1丈等于10尺)( )
A.2丈4尺 B.2丈5尺 C.2丈6尺 D.2丈8尺
9.已知圆柱的轴截面是正方形,其面积为Q,则它的一个底面的面积为( )
A.Q B. C. D.
10.将一个等腰梯形绕它的较长的底边所在的直线旋转一周,所得的几何体包括( )
A.一个圆柱、两个圆锥 B.两个圆台、一个圆柱
C.两个圆柱、一个圆台 D.一个圆台、两个圆锥
11.“四棱柱是直四棱柱”是“四棱柱的底面是矩形”的_________条件.
12.已知球O的半径为5,球内一点M到球心O的距离为4,过点M的平面截球的截面面积为S,则S的最小值为________.
13.已知圆柱的底面半径为1,若圆柱的侧面展开图的面积为,则圆柱的高为___________.
14.一个正三角形和它的内切圆如图所示,将阴影部分绕直线l旋转得到一个几何体,请描述该几何体的结构特征.
答案以及解析
1.答案:B
解析:对于A,棱柱的上下底面可以是三角形或者是梯形,故A不正确;对于B,面最少的就是三棱柱,共有五个面,B正确;对于C,长方体是棱柱,但是上下、左右、前后都是互相平行的,C不正确;对于D,斜棱柱的侧面可以不是矩形,D错误,故选B.
2.答案:B
解析:根据题意,顶点数就是碳原子数即为70,每个碳原子被3条棱长共用,故棱长数,设正五边形x个,正六边形y个,则,,解得,,故正六边形个数为25个,即六元环的个数为25个,故选B.
3.答案:A
解析:由圆锥的定义可知A选项是圆锥.
4.答案:D
解析:观察图形可知,D不是旋转体.
5.答案:A
解析:如图,是A在底面的射影,由正弦定理得,的外接圆半径,
由勾股定理得棱锥的高,
设球O的半径为R,则,
解得,所以,
在中,由余弦定理得,
所以,所以在中,,
当截面垂直于OE时,截面面积最小,此时半径为,截面面积为.
故选:A.
6.答案:B
解析:①②正确,③④错误,故选B.
7.答案:B
解析:球只有一个曲面,故①错,②对,③对.由于几何体是空间图形,故一定有面,④错.
8.答案:C
解析:由题意,圆柱的侧面展开图是矩形,一条直角边(即圆木的高)长24尺,另一条直角边长(尺),因此葛藤长的最小值为(尺),即为2丈6尺.故选C.
9.答案:C
解析:圆柱的轴截面一边为高,另一边为底面的直径,由轴截面为正方形可知,高与底面直径均为,所以底面半径为,所以底面的面积为.
10.答案:A
解析:将等腰梯形分割成两个直角三角形和一个矩形,如图所示.矩形绕其一边旋转一周得到圆柱,直角三角形绕其一条直角边旋转一周得到圆锥.因此,将该等腰梯形绕它的较长的底边所在的直线旋转一周,可得几何体包括一个圆柱、两个圆锥.故选A.
11.答案:既不充分也不必要
解析:若四棱柱是直四棱柱,只需四棱柱的侧棱垂直底面,但底面不一定是矩形,即充分性不成立;
反之:底面为矩形的四棱柱不一定为直四棱柱,即必要性不成立,
所以“四棱柱是直四棱柱”是“四棱柱的底面是矩形”的既不充分也不必要条件.
故答案为:既不充分也不必要
12.答案:
解析:解:设球的半径为R,截面面积最小的半径为r,由题意可得所以当OM垂直于截面时,截面的半径最小,即截面的面积最小,由,所以截面的面积的最小值为.故答案为:.
13.答案:4
解析:设圆柱的高为,有,得
14.答案:正三角形三边绕直线l旋转形成的面所围成的几何体是圆锥,圆绕直线l旋转形成的面所围成的几何体是球体,所以将阴影部分绕直线l旋转得到的几何体是圆锥挖去一个与圆锥底面和侧面均相切的球.
1.下列命题正确的是( )
A.棱柱的每个面都是平行四边形 B.一个棱柱至少有五个面
C.棱柱有且只有两个面互相平行 D.棱柱的侧面都是矩形
2.碳是一种碳原子族,可高效杀灭癌细胞,它是由70个碳原子构成的,其结构是由五元环(正五边形面)和六元环(正六边形面)组成的封闭的凸多面体,共37个面,则其六元环的个数为( )
A.12 B.25 C.30 D.36
3.下列几何体中为圆锥的是( )
A. B. C. D.
4.下列几何体中不是旋转体的是( )
A. B. C. D.
5.已知球O是正三棱锥(底面是正三角形,顶点在底面的射影为底面中心)的外接球,,,点E在线段BD上,且.过点E作球O的截面,则所得截面面积的最小值是( )
A. B. C. D.
6.下列关于棱柱的命题中,真命题的个数是( )
①同一棱柱的侧棱平行且相等;
②一个棱柱至少有5个面;
③当棱柱的底面是正多边形时,该棱柱一定是正棱柱;
④当棱柱的底面是等腰梯形时,该棱柱一定是平行六面体.
A.1 B.2 C.3 D.4
7.给出下列说法:
①任何一个几何体都必须有顶点、棱和面;
②一个几何体可以没有顶点;
③一个几何体可以没有棱;
④一个几何体可以没有面.
其中正确的个数是( )
A.1 B.2 C.3 D.4
8.在我国古代数学名著中有这样一个问题:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周长为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺?”这个问题中,葛藤长的最小值为(注:1丈等于10尺)( )
A.2丈4尺 B.2丈5尺 C.2丈6尺 D.2丈8尺
9.已知圆柱的轴截面是正方形,其面积为Q,则它的一个底面的面积为( )
A.Q B. C. D.
10.将一个等腰梯形绕它的较长的底边所在的直线旋转一周,所得的几何体包括( )
A.一个圆柱、两个圆锥 B.两个圆台、一个圆柱
C.两个圆柱、一个圆台 D.一个圆台、两个圆锥
11.“四棱柱是直四棱柱”是“四棱柱的底面是矩形”的_________条件.
12.已知球O的半径为5,球内一点M到球心O的距离为4,过点M的平面截球的截面面积为S,则S的最小值为________.
13.已知圆柱的底面半径为1,若圆柱的侧面展开图的面积为,则圆柱的高为___________.
14.一个正三角形和它的内切圆如图所示,将阴影部分绕直线l旋转得到一个几何体,请描述该几何体的结构特征.
答案以及解析
1.答案:B
解析:对于A,棱柱的上下底面可以是三角形或者是梯形,故A不正确;对于B,面最少的就是三棱柱,共有五个面,B正确;对于C,长方体是棱柱,但是上下、左右、前后都是互相平行的,C不正确;对于D,斜棱柱的侧面可以不是矩形,D错误,故选B.
2.答案:B
解析:根据题意,顶点数就是碳原子数即为70,每个碳原子被3条棱长共用,故棱长数,设正五边形x个,正六边形y个,则,,解得,,故正六边形个数为25个,即六元环的个数为25个,故选B.
3.答案:A
解析:由圆锥的定义可知A选项是圆锥.
4.答案:D
解析:观察图形可知,D不是旋转体.
5.答案:A
解析:如图,是A在底面的射影,由正弦定理得,的外接圆半径,
由勾股定理得棱锥的高,
设球O的半径为R,则,
解得,所以,
在中,由余弦定理得,
所以,所以在中,,
当截面垂直于OE时,截面面积最小,此时半径为,截面面积为.
故选:A.
6.答案:B
解析:①②正确,③④错误,故选B.
7.答案:B
解析:球只有一个曲面,故①错,②对,③对.由于几何体是空间图形,故一定有面,④错.
8.答案:C
解析:由题意,圆柱的侧面展开图是矩形,一条直角边(即圆木的高)长24尺,另一条直角边长(尺),因此葛藤长的最小值为(尺),即为2丈6尺.故选C.
9.答案:C
解析:圆柱的轴截面一边为高,另一边为底面的直径,由轴截面为正方形可知,高与底面直径均为,所以底面半径为,所以底面的面积为.
10.答案:A
解析:将等腰梯形分割成两个直角三角形和一个矩形,如图所示.矩形绕其一边旋转一周得到圆柱,直角三角形绕其一条直角边旋转一周得到圆锥.因此,将该等腰梯形绕它的较长的底边所在的直线旋转一周,可得几何体包括一个圆柱、两个圆锥.故选A.
11.答案:既不充分也不必要
解析:若四棱柱是直四棱柱,只需四棱柱的侧棱垂直底面,但底面不一定是矩形,即充分性不成立;
反之:底面为矩形的四棱柱不一定为直四棱柱,即必要性不成立,
所以“四棱柱是直四棱柱”是“四棱柱的底面是矩形”的既不充分也不必要条件.
故答案为:既不充分也不必要
12.答案:
解析:解:设球的半径为R,截面面积最小的半径为r,由题意可得所以当OM垂直于截面时,截面的半径最小,即截面的面积最小,由,所以截面的面积的最小值为.故答案为:.
13.答案:4
解析:设圆柱的高为,有,得
14.答案:正三角形三边绕直线l旋转形成的面所围成的几何体是圆锥,圆绕直线l旋转形成的面所围成的几何体是球体,所以将阴影部分绕直线l旋转得到的几何体是圆锥挖去一个与圆锥底面和侧面均相切的球.
