高中数学苏教版(2022春 )选择性必修第二册 8.3 正态分布(72张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 8.3 正态分布(72张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 11:36:33 | ||
图片预览









文档简介
(共72张PPT)
§8.3 正态分布
第8章 概 率
1.利用实际问题的频率分布直方图,了解正态密度曲线的特点及
曲线所表示的意义.
2.了解变量落在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ
+3σ)内的概率大小.
3.掌握正态分布与标准正态分布的转换,能利用标准正态分布表
求得标准正态分布在某一区间内取值的概率.
学习目标
一所学校同年级的同学的身高,特别高的同学比较少,特别矮的同学也不多,大都集中在某个高度左右;某种电子产品的使用寿命也都接近某一个数,使用期过长,或过短的产品相对较少.生活中这样的现象很多,是否可以用数学模型来刻画呢?
导语
某乒乓球生产厂家生产一批直径为4.8 cm的乒乓球,如果通过抽样估计得到这批乒乓球的直径的标准差为0.1,则应该怎样来判断这批乒乓球的质量?如果产品中发现一个乒乓球的直径为5.2 cm,则说明了什么情况?
随堂演练
课时对点练
一、正态曲线及其性质
二、正态总体在三个特殊区间内取值的概率值
三、标准正态分布
内容索引
一、正态曲线及其性质
问题 你见过高尔顿板吗?如图所示是一块高尔顿板示意图.在一块木板上钉上若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内.
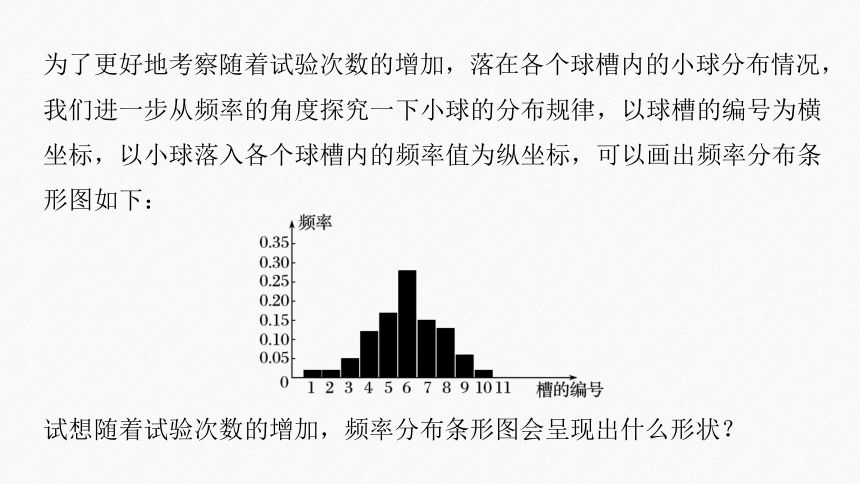
为了更好地考察随着试验次数的增加,落在各个球槽内的小球分布情况,我们进一步从频率的角度探究一下小球的分布规律,以球槽的编号为横坐标,以小球落入各个球槽内的频率值为纵坐标,可以画出频率分布条形图如下:
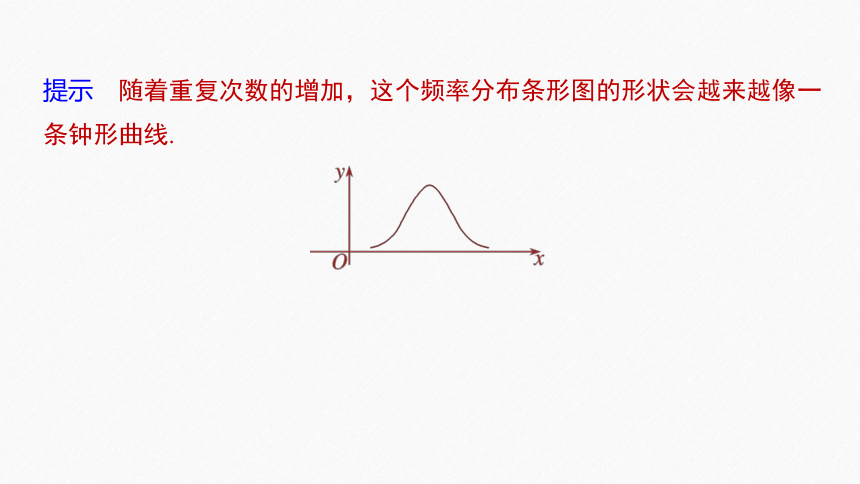
试想随着试验次数的增加,频率分布条形图会呈现出什么形状?
提示 随着重复次数的增加,这个频率分布条形图的形状会越来越像一条钟形曲线.
知识梳理
1.概率密度曲线
对于某一随机变量的频率分布直方图,如果数据无限 且组距无限
,那么频率分布直方图上的折线将趋于一条光滑的曲线,我们将此曲线称为概率密度曲线.
增多
缩小
2.正态密度曲线
上升
下降
x轴
大
小
1
函数表达式 P(x)= ,x∈R,其中实数μ(μ∈R)和σ(σ>0)为参数
图象的特征 (1)当x<μ时,曲线 ;当x>μ时,曲线 .当曲线向左右两边无限延伸时,以 为渐近线;
(2)曲线关于直线 对称;
(3)σ越 ,曲线越扁平;σ越 ,曲线越尖陡;
(4)在曲线下方和x轴上方范围内的区域面积为__
x=μ
3.正态分布
若X是一个随机变量,则对任给区间(a,b],P(a和 所围成的图形的面积,我们就称随机变量X服从参数为μ和σ2的正态分布,简记为 .
正态密度曲线
x轴上(a,b]上方
下方
X~N(μ,σ2)
注意点:
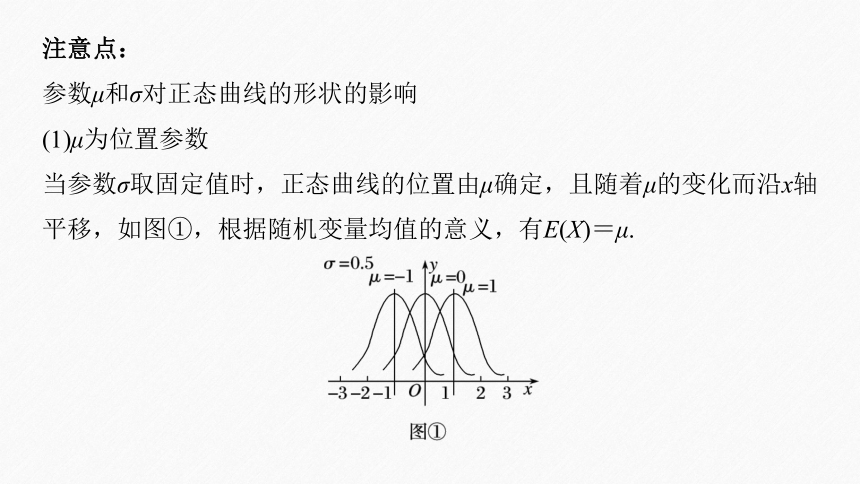
参数μ和σ对正态曲线的形状的影响
(1)μ为位置参数
当参数σ取固定值时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移,如图①,根据随机变量均值的意义,有E(X)=μ.
(2)σ为形状参数
参数σ的大小决定了曲线的高低和胖瘦,因此σ的变化影响曲线的形状,σ越小,曲线越“瘦高”,表示随机变量的分布越集中;σ越大,曲线越“矮胖”,表示随机变量的分布越分散,如图②,根据随机变量方差的意义,有V(X)=σ2.
√
解析 函数f(x)图象的对称轴为直线x=μ,因为μ<0,所以排除B,D;
又正态曲线位于x轴上方,因此排除C.
A.μ1<μ2=μ3,σ1=σ2>σ3
B.μ1>μ2=μ3,σ1=σ2<σ3
C.μ1=μ2<μ3,σ1<σ2=σ3
D.μ1<μ2=μ3,σ1=σ2<σ3
√
解析 由正态曲线关于直线x=μ对称,知μ1<μ2=μ3,σ的大小决定曲线的形状,σ越大,随机变量的分布越分散,曲线越“矮胖”;σ越小,随机变量的分布越集中,曲线越“瘦高”,则σ1=σ2<σ3.
反思感悟 利用正态曲线的特点求参数μ,σ
(1)正态曲线是单峰的,它关于直线x=μ对称,由此特点结合图象求出μ.
跟踪训练1 (1)如图所示分别是甲、乙、丙三种品牌石英钟时间误差分布的正态曲线,则下列说法不正确的是
A.三种品牌的石英钟时间误差的均值相等
B.时间误差的均值从大到小依次为甲、乙、丙
C.时间误差的方差从小到大依次为甲、乙、丙
D.三种品牌的石英钟中甲品牌的质量最好
√
解析 正态曲线中的参数μ,σ分别表示随机变量的均值和标准差.由图象可知甲、乙、丙三种曲线的对称轴相同,故它们的时间误差的均值相等,A正确,B错误;
再根据图象的扁平与尖陡情况可以判断它们的标准差从小到大依次为甲、乙、丙,这也说明甲品牌偏离均值的离散程度较小,所以甲品牌的质量最好,故C,D正确.
A.甲类水果的平均质量μ1=0.4 kg
B.甲类水果的质量比乙类水果的质量更集中于平
均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数σ2=1.99
√
√
√
解析 由图象可知甲图象关于直线x=0.4对称,乙图象关于直线x=0.8对称,
所以μ1=0.4,μ2=0.8,μ1<μ2,故A,C正确;
因为甲图象比乙图象更“高瘦”,所以甲类水果的质量比乙类水果的质量更集中于平均值左右,故B正确;
因为乙图象的最大值为1.99,
二、正态总体在三个特殊区间内取值的概率值
知识梳理
(1)落在区间(μ-σ,μ+σ)内的概率约为 .
(2)落在区间(μ-2σ,μ+2σ)内的概率约为 .
(3)落在区间(μ-3σ,μ+3σ)内的概率约为 .
注意点:
尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间(μ-3σ,μ+3σ)内,而在此区间以外取值的概率大约只有0.003,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)中的值,这在统计学中称为3σ原则.
68.3%
95.4%
99.7%
例2 设ξ~N(1,22),试求:
(1)P(-1<ξ<3);
解 ∵ξ~N(1,22),∴μ=1,σ=2.
P(-1<ξ<3)=P(1-2<ξ<1+2)
=P(μ-σ<ξ<μ+σ)≈0.683;
(2)P(3<ξ<5).
解 ∵P(3<ξ<5)=P(-3<ξ<-1),
延伸探究 若本例条件不变,求P(ξ≥5).
反思感悟 充分利用正态曲线的对称性及面积为1的性质求解
(1)熟记正态曲线关于直线x=μ对称,从而在关于x=μ对称的区间上概率相等.
(2)P(Xμ+a).
跟踪训练2 为了解某省高中男生的身体发育情况,随机抽取1 000名男生测量他们的体重,测量的结果表明他们的体重X(单位:kg)服从正态分布N(μ,22),正态曲线如图所示.若体重落在区间(58.5,62.5)内属于正常情况,则在这1 000名男生中不属于正常情况的人数约是
A.954
B.819
C.683
D.317
解析 由题意可知,μ=60.5,σ=2,故P(58.5√
三、标准正态分布
知识梳理
N(0,1)
例3 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩ξ近似服从正态分布N(70,100).已知成绩在90分以上(含90分)的学生有12名.
(1)此次参赛的学生总数约为多少人?
解 因为ξ~N(70,100),
=1-Φ(2)=1-0.977 2=0.022 8.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,
(2)若该校计划奖励竞赛成绩排在前50名的学生,则设奖的分数线约为多少分?
参考数据:可供查阅的(部分)标准正态分布表Φ(Z)
x0 0 1 2 3 4 5 6 7 8 9
1.2 0.884 9 0.886 9 0.888 0.890 77 0.892 5 0.894 4 0.896 2 0.898 0 0.899 7 0.901 5
1.3 0.903 2 0.904 9 0.906 6 0.908 2 0.909 9 0.911 5 0.913 1 0.914 7 0.916 2 0.917 7
1.4 0.919 2 0.920 7 0.922 2 0.923 6 0.925 1 0.926 5 0.927 8 0.929 2 0.930 6 0.931 6
1.9 0.977 13 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0 0.975 6 0.976 2 0.976 7
2.0 0.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7
2.1 0.982 1 0.982 6 0.983 0 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0 0.985 4 0.985 7
解 假定设奖的分数线为x分,则X~N(70,100),
解得x=83.1.故设奖的分数线约为83分.
(2)Φ(a)=P(x跟踪训练3 某市统考成绩大体上反映了全市学生的成绩状况,因此可以把统考成绩作为总体,设平均成绩μ=480,标准差σ=100,总体服从正态分布,若全市重点校录取率为40%,那么重点录取分数线可能划在多少分?(已知Φ(0.25)=0.6)
解 ∵平均成绩μ=480,标准差σ=100,总体服从正态分布,
∴X~N(480,1002).设重点录取分数线可能划在f分,
1.知识清单:
(1)正态曲线及其特点.
(2)正态分布及正态总体在三个特殊区间内取值的概率值.
(3) 正态分布与标准正态分布的转化.
2.方法归纳:转化化归、数形结合.
3.常见误区:概率区间转化不等价.
课堂小结
随堂演练
1
2
3
4
√
1
2
3
4
2.(多选)下面给出的关于正态曲线的4个叙述中,正确的有
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
解析 只有C错误,因为当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,总体分布越集中;σ越大,曲线越“矮胖”,总体分布越分散.
√
√
√
1
2
3
4
3.已知服从正态分布N(μ,σ2)的随机变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ)和(μ-3σ,μ+3σ)内取值的概率约为68.3%,95.4%和99.7%.若某校高一年级1 000名学生的某次考试成绩X服从正态分布N(90,152),则此次考试成绩在区间(60,120)内的学生大约有
A.997人 B.972人
C.954人 D.683人
√
解析 依题意可知μ=90,σ=15,故P(601 000×0.954=954,故学生大约有954人.
1
2
3
4
4.设随机变量X~N(2,9),若P(X>1+c)=P(X则:(1)c=___,
解析 由X~N(2,9)可知,正态密度曲线图象关于直线x=2对称(如图所示),
2
又P(X>1+c)=P(X故有2-(c-1)=(c+1)-2,
∴c=2.
1
2
3
4
(2)P(-40.954
解析 P(-4课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
2.已知随机变量X服从正态分布N(a,4),且P(X>1)=0.5,则实数a的值为
A.1 B.2 C.3 D.4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 随机变量X服从正态分布N(a,4),所以曲线关于x=a对称,且P(X>a)=0.5,由P(X>1)=0.5,可知μ=a=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(多选)一次教学质量检测中,甲、乙、丙三科考试成绩的正态分布密度曲线如图所示,下列说法中不正确的是
解析 由题中图象可知三科总体的均值相等,由正态分布密度曲线的性质,可知σ越大,正态曲线越“矮胖”,σ越小,正态曲线越“瘦高”,故三科总体的标准差从小到大依次为甲、乙、丙.
A.甲科总体的标准差最小
B.丙科总体的均值最小
C.乙科总体的标准差及均值都比甲小,比丙大
D.甲、乙、丙总体的均值不相同
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)等于
A.0.6 B.0.4 C.0.3 D.0.2
√
解析 ∵随机变量ξ服从正态分布N(2,σ2),
∴μ=2,对称轴是ξ=2.
∵P(ξ<4)=0.8,
∴P(ξ≥4)=P(ξ≤0)=0.2,
∴P(0<ξ<4)=0.6,
∴P(0<ξ<2)=0.3.故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.某厂生产的零件外径X~N(10,0.04),今从该厂上午、下午生产的零件中各取一件,测得其外径分别为9.9 cm,9.3 cm,则可认为
A.上午生产情况正常,下午生产情况异常
B.上午生产情况异常,下午生产情况正常
C.上午、下午生产情况均正常
D.上午、下午生产情况均异常
解析 因测量值X为随机变量,又X~N(10,0.04),
所以μ=10,σ=0.2,
记I=(μ-3σ,μ+3σ)=(9.4,10.6),
则9.9∈I,9.3 I.故选A.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)设随机变量ξ服从正态分布N(0,1),则下列结论正确的是
A.P(|ξ|-a)(a>0)
B.P(|ξ|0)
C.P(|ξ|0)
D.P(|ξ|0)
√
√
解析 因为P(|ξ|因为P(|ξ|a)=P(ξ因为P(|ξ|0),所以D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设随机变量X~N(4,σ2),且P(40.2
解析 概率密度曲线关于直线X=4对称,在4右边的概率为0.5,在0左边的概率等于8右边的概率,即0.5-0.3=0.2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设随机变量X服从标准正态分布N(0,1),在某项测量中,已知X在(-∞,-1.96]内取值的概率为0.025,则P(|X|<1.96)=________.
0.95
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 ∵X~N(0,1),
∴P(|X|<1.96)=P(-1.96=Φ(1.96)-Φ(-1.96)=1-2Φ(-1.96)=0.95.
方法二 因为曲线的对称轴是直线X=0,所以由图知
P(X>1.96)=P(X≤-1.96)=Φ(-1.96)=0.025,
∴P(|X|<1.96)=1-0.025-0.025=0.95.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.设X~N(3,42),试求:
(1)P(-1解 ∵X~N(3,42),
∴μ=3,σ=4.
P(-11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)P(7解 ∵P(71
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)P(X≥11).
解 ∵P(X≥11)=P(X≤-5),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.某人骑自行车上班,第一条路线较短但拥挤,到达时间X(分钟)服从正态分布N(5,1);第二条路线较长不拥挤,X服从N(6,0.16).若有一天他出发时离点名时间还有7分钟,问他应选哪一条路线?若离点名时间还有6.5分钟,问他应选哪一条路线?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 还有7分钟时:
若选第一条路线,即X~N(5,1),
能及时到达的概率
P1=P(X≤7)=P(X≤5)+P(5若选第二条路线,即X~N(6,0.16),
能及时到达的概率
P2=P(X≤7)=P(X≤6)+P(61
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为P1同理,还有6.5分钟时,应选第一条路线.
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.在某市的高三质量检测考试中,数学成绩服从正态分布N(98,100).已知参加本次考试的全市学生约有9 450人,如果某学生在这次考试中的数学成绩是108分,那么他的数学成绩大约排在全市第
A.1 498名 B.1 700名 C.4 500名 D.8 000名
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.一批电阻的电阻值X(单位:Ω)服从正态分布N(1 000,52),现从甲、乙两箱出厂的成品中各随机抽取一个电阻,测得电阻值分别为1 011 Ω和982 Ω,可以认为
A.甲、乙两箱电阻均可出厂
B.甲、乙两箱电阻均不可出厂
C.甲箱电阻可出厂,乙箱电阻不可出厂
D.甲箱电阻不可出厂,乙箱电阻可出厂
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵X~N(1 000,52),∴μ=1 000,σ=5,
∴μ-3σ=1 000-3×5=985,
μ+3σ=1 000+3×5=1 015.
∵1 011∈(985,1 015),982 (985,1 015),
∴甲箱电阻可出厂,乙箱电阻不可出厂.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.某工厂生产一种螺栓,在正常情况下,螺栓的直径X(单位:mm)服从正态分布X~N(100,1).现加工10个螺栓的尺寸(单位:mm)如下:101.7,100.3,99.6,102.4,98.2,103.2,101.1,98.8,100.4,100.0.X~N(μ,σ2),有P(μ-2σ√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知随机变量X~N(2,22),且aX+b(a>0)服从标准正态分布N(0,1),则
a=____,b=____.
-1
解析 ∵随机变量X~N(2,22),
∴E(X)=2,D(X)=22=4.
∴E(aX+b)=aE(X)+b=2a+b=0,
D(aX+b)=a2D(X)=4a2=1,
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.P(Y≥μ2)≥P(Y≥μ1)
B.P(X≤σ2)≤P(X≤σ1)
C.对任意正数t,P(X≤t)>P(Y≤t)
D.对任意正数t,P(X>t)>P(Y>t)
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题图可知μ1<0<μ2,σ1<σ2,
∴P(Y≥μ2)P(X≤σ2)>P(X≤σ1),故B错;
当t为任意正数时,由题图可知P(X≤t)>P(Y≤t),
而P(X≤t)=1-P(X>t),P(Y≤t)=1-P(Y>t),
∴P(X>t)t),故C正确,D错.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某高校为了解全校学生的阅读情况,随机调查了200名学生每周阅读时间X(单位:小时)并绘制如图所示的频率分布直方图.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
s2=(6-9)2×0.03+(7-9)2×0.1+(8-9)2×0.2+(9-9)2×0.35+(10-9)2×0.19+(11-9)2×0.09+(12-9)2×0.04=1.78.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由(1)知μ=9,σ2=1.78,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②从该高校的学生中随机抽取20名,记Z表示这20名学生中每周阅读时间超过10小时的人数,求P(Z≥2)(结果精确到0.000 1)以及Z的均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由①知P(X>10)=1-P(X≤10)=0.226 6,
可得Z~B(20,0.226 6),
P(Z≥2)=1-P(Z=0)-P(Z=1)
=1-(0.773 4+20×0.226 6)×0.007 6
≈0.959 7.
∴Z的均值E(Z)=20×0.226 6=4.532.
本课结束
§8.3 正态分布
第8章 概 率
1.利用实际问题的频率分布直方图,了解正态密度曲线的特点及
曲线所表示的意义.
2.了解变量落在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ
+3σ)内的概率大小.
3.掌握正态分布与标准正态分布的转换,能利用标准正态分布表
求得标准正态分布在某一区间内取值的概率.
学习目标
一所学校同年级的同学的身高,特别高的同学比较少,特别矮的同学也不多,大都集中在某个高度左右;某种电子产品的使用寿命也都接近某一个数,使用期过长,或过短的产品相对较少.生活中这样的现象很多,是否可以用数学模型来刻画呢?
导语
某乒乓球生产厂家生产一批直径为4.8 cm的乒乓球,如果通过抽样估计得到这批乒乓球的直径的标准差为0.1,则应该怎样来判断这批乒乓球的质量?如果产品中发现一个乒乓球的直径为5.2 cm,则说明了什么情况?
随堂演练
课时对点练
一、正态曲线及其性质
二、正态总体在三个特殊区间内取值的概率值
三、标准正态分布
内容索引
一、正态曲线及其性质
问题 你见过高尔顿板吗?如图所示是一块高尔顿板示意图.在一块木板上钉上若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内.
为了更好地考察随着试验次数的增加,落在各个球槽内的小球分布情况,我们进一步从频率的角度探究一下小球的分布规律,以球槽的编号为横坐标,以小球落入各个球槽内的频率值为纵坐标,可以画出频率分布条形图如下:
试想随着试验次数的增加,频率分布条形图会呈现出什么形状?
提示 随着重复次数的增加,这个频率分布条形图的形状会越来越像一条钟形曲线.
知识梳理
1.概率密度曲线
对于某一随机变量的频率分布直方图,如果数据无限 且组距无限
,那么频率分布直方图上的折线将趋于一条光滑的曲线,我们将此曲线称为概率密度曲线.
增多
缩小
2.正态密度曲线
上升
下降
x轴
大
小
1
函数表达式 P(x)= ,x∈R,其中实数μ(μ∈R)和σ(σ>0)为参数
图象的特征 (1)当x<μ时,曲线 ;当x>μ时,曲线 .当曲线向左右两边无限延伸时,以 为渐近线;
(2)曲线关于直线 对称;
(3)σ越 ,曲线越扁平;σ越 ,曲线越尖陡;
(4)在曲线下方和x轴上方范围内的区域面积为__
x=μ
3.正态分布
若X是一个随机变量,则对任给区间(a,b],P(a
正态密度曲线
x轴上(a,b]上方
下方
X~N(μ,σ2)
注意点:
参数μ和σ对正态曲线的形状的影响
(1)μ为位置参数
当参数σ取固定值时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移,如图①,根据随机变量均值的意义,有E(X)=μ.
(2)σ为形状参数
参数σ的大小决定了曲线的高低和胖瘦,因此σ的变化影响曲线的形状,σ越小,曲线越“瘦高”,表示随机变量的分布越集中;σ越大,曲线越“矮胖”,表示随机变量的分布越分散,如图②,根据随机变量方差的意义,有V(X)=σ2.
√
解析 函数f(x)图象的对称轴为直线x=μ,因为μ<0,所以排除B,D;
又正态曲线位于x轴上方,因此排除C.
A.μ1<μ2=μ3,σ1=σ2>σ3
B.μ1>μ2=μ3,σ1=σ2<σ3
C.μ1=μ2<μ3,σ1<σ2=σ3
D.μ1<μ2=μ3,σ1=σ2<σ3
√
解析 由正态曲线关于直线x=μ对称,知μ1<μ2=μ3,σ的大小决定曲线的形状,σ越大,随机变量的分布越分散,曲线越“矮胖”;σ越小,随机变量的分布越集中,曲线越“瘦高”,则σ1=σ2<σ3.
反思感悟 利用正态曲线的特点求参数μ,σ
(1)正态曲线是单峰的,它关于直线x=μ对称,由此特点结合图象求出μ.
跟踪训练1 (1)如图所示分别是甲、乙、丙三种品牌石英钟时间误差分布的正态曲线,则下列说法不正确的是
A.三种品牌的石英钟时间误差的均值相等
B.时间误差的均值从大到小依次为甲、乙、丙
C.时间误差的方差从小到大依次为甲、乙、丙
D.三种品牌的石英钟中甲品牌的质量最好
√
解析 正态曲线中的参数μ,σ分别表示随机变量的均值和标准差.由图象可知甲、乙、丙三种曲线的对称轴相同,故它们的时间误差的均值相等,A正确,B错误;
再根据图象的扁平与尖陡情况可以判断它们的标准差从小到大依次为甲、乙、丙,这也说明甲品牌偏离均值的离散程度较小,所以甲品牌的质量最好,故C,D正确.
A.甲类水果的平均质量μ1=0.4 kg
B.甲类水果的质量比乙类水果的质量更集中于平
均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数σ2=1.99
√
√
√
解析 由图象可知甲图象关于直线x=0.4对称,乙图象关于直线x=0.8对称,
所以μ1=0.4,μ2=0.8,μ1<μ2,故A,C正确;
因为甲图象比乙图象更“高瘦”,所以甲类水果的质量比乙类水果的质量更集中于平均值左右,故B正确;
因为乙图象的最大值为1.99,
二、正态总体在三个特殊区间内取值的概率值
知识梳理
(1)落在区间(μ-σ,μ+σ)内的概率约为 .
(2)落在区间(μ-2σ,μ+2σ)内的概率约为 .
(3)落在区间(μ-3σ,μ+3σ)内的概率约为 .
注意点:
尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间(μ-3σ,μ+3σ)内,而在此区间以外取值的概率大约只有0.003,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)中的值,这在统计学中称为3σ原则.
68.3%
95.4%
99.7%
例2 设ξ~N(1,22),试求:
(1)P(-1<ξ<3);
解 ∵ξ~N(1,22),∴μ=1,σ=2.
P(-1<ξ<3)=P(1-2<ξ<1+2)
=P(μ-σ<ξ<μ+σ)≈0.683;
(2)P(3<ξ<5).
解 ∵P(3<ξ<5)=P(-3<ξ<-1),
延伸探究 若本例条件不变,求P(ξ≥5).
反思感悟 充分利用正态曲线的对称性及面积为1的性质求解
(1)熟记正态曲线关于直线x=μ对称,从而在关于x=μ对称的区间上概率相等.
(2)P(X
跟踪训练2 为了解某省高中男生的身体发育情况,随机抽取1 000名男生测量他们的体重,测量的结果表明他们的体重X(单位:kg)服从正态分布N(μ,22),正态曲线如图所示.若体重落在区间(58.5,62.5)内属于正常情况,则在这1 000名男生中不属于正常情况的人数约是
A.954
B.819
C.683
D.317
解析 由题意可知,μ=60.5,σ=2,故P(58.5
三、标准正态分布
知识梳理
N(0,1)
例3 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩ξ近似服从正态分布N(70,100).已知成绩在90分以上(含90分)的学生有12名.
(1)此次参赛的学生总数约为多少人?
解 因为ξ~N(70,100),
=1-Φ(2)=1-0.977 2=0.022 8.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,
(2)若该校计划奖励竞赛成绩排在前50名的学生,则设奖的分数线约为多少分?
参考数据:可供查阅的(部分)标准正态分布表Φ(Z)
x0 0 1 2 3 4 5 6 7 8 9
1.2 0.884 9 0.886 9 0.888 0.890 77 0.892 5 0.894 4 0.896 2 0.898 0 0.899 7 0.901 5
1.3 0.903 2 0.904 9 0.906 6 0.908 2 0.909 9 0.911 5 0.913 1 0.914 7 0.916 2 0.917 7
1.4 0.919 2 0.920 7 0.922 2 0.923 6 0.925 1 0.926 5 0.927 8 0.929 2 0.930 6 0.931 6
1.9 0.977 13 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0 0.975 6 0.976 2 0.976 7
2.0 0.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7
2.1 0.982 1 0.982 6 0.983 0 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0 0.985 4 0.985 7
解 假定设奖的分数线为x分,则X~N(70,100),
解得x=83.1.故设奖的分数线约为83分.
(2)Φ(a)=P(x
解 ∵平均成绩μ=480,标准差σ=100,总体服从正态分布,
∴X~N(480,1002).设重点录取分数线可能划在f分,
1.知识清单:
(1)正态曲线及其特点.
(2)正态分布及正态总体在三个特殊区间内取值的概率值.
(3) 正态分布与标准正态分布的转化.
2.方法归纳:转化化归、数形结合.
3.常见误区:概率区间转化不等价.
课堂小结
随堂演练
1
2
3
4
√
1
2
3
4
2.(多选)下面给出的关于正态曲线的4个叙述中,正确的有
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
解析 只有C错误,因为当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,总体分布越集中;σ越大,曲线越“矮胖”,总体分布越分散.
√
√
√
1
2
3
4
3.已知服从正态分布N(μ,σ2)的随机变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ)和(μ-3σ,μ+3σ)内取值的概率约为68.3%,95.4%和99.7%.若某校高一年级1 000名学生的某次考试成绩X服从正态分布N(90,152),则此次考试成绩在区间(60,120)内的学生大约有
A.997人 B.972人
C.954人 D.683人
√
解析 依题意可知μ=90,σ=15,故P(60
1
2
3
4
4.设随机变量X~N(2,9),若P(X>1+c)=P(X
解析 由X~N(2,9)可知,正态密度曲线图象关于直线x=2对称(如图所示),
2
又P(X>1+c)=P(X
∴c=2.
1
2
3
4
(2)P(-4
解析 P(-4
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
2.已知随机变量X服从正态分布N(a,4),且P(X>1)=0.5,则实数a的值为
A.1 B.2 C.3 D.4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 随机变量X服从正态分布N(a,4),所以曲线关于x=a对称,且P(X>a)=0.5,由P(X>1)=0.5,可知μ=a=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(多选)一次教学质量检测中,甲、乙、丙三科考试成绩的正态分布密度曲线如图所示,下列说法中不正确的是
解析 由题中图象可知三科总体的均值相等,由正态分布密度曲线的性质,可知σ越大,正态曲线越“矮胖”,σ越小,正态曲线越“瘦高”,故三科总体的标准差从小到大依次为甲、乙、丙.
A.甲科总体的标准差最小
B.丙科总体的均值最小
C.乙科总体的标准差及均值都比甲小,比丙大
D.甲、乙、丙总体的均值不相同
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)等于
A.0.6 B.0.4 C.0.3 D.0.2
√
解析 ∵随机变量ξ服从正态分布N(2,σ2),
∴μ=2,对称轴是ξ=2.
∵P(ξ<4)=0.8,
∴P(ξ≥4)=P(ξ≤0)=0.2,
∴P(0<ξ<4)=0.6,
∴P(0<ξ<2)=0.3.故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.某厂生产的零件外径X~N(10,0.04),今从该厂上午、下午生产的零件中各取一件,测得其外径分别为9.9 cm,9.3 cm,则可认为
A.上午生产情况正常,下午生产情况异常
B.上午生产情况异常,下午生产情况正常
C.上午、下午生产情况均正常
D.上午、下午生产情况均异常
解析 因测量值X为随机变量,又X~N(10,0.04),
所以μ=10,σ=0.2,
记I=(μ-3σ,μ+3σ)=(9.4,10.6),
则9.9∈I,9.3 I.故选A.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)设随机变量ξ服从正态分布N(0,1),则下列结论正确的是
A.P(|ξ|
B.P(|ξ|
C.P(|ξ|
D.P(|ξ|
√
√
解析 因为P(|ξ|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设随机变量X~N(4,σ2),且P(4
解析 概率密度曲线关于直线X=4对称,在4右边的概率为0.5,在0左边的概率等于8右边的概率,即0.5-0.3=0.2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设随机变量X服从标准正态分布N(0,1),在某项测量中,已知X在(-∞,-1.96]内取值的概率为0.025,则P(|X|<1.96)=________.
0.95
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 ∵X~N(0,1),
∴P(|X|<1.96)=P(-1.96
方法二 因为曲线的对称轴是直线X=0,所以由图知
P(X>1.96)=P(X≤-1.96)=Φ(-1.96)=0.025,
∴P(|X|<1.96)=1-0.025-0.025=0.95.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.设X~N(3,42),试求:
(1)P(-1
∴μ=3,σ=4.
P(-1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)P(7
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)P(X≥11).
解 ∵P(X≥11)=P(X≤-5),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.某人骑自行车上班,第一条路线较短但拥挤,到达时间X(分钟)服从正态分布N(5,1);第二条路线较长不拥挤,X服从N(6,0.16).若有一天他出发时离点名时间还有7分钟,问他应选哪一条路线?若离点名时间还有6.5分钟,问他应选哪一条路线?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 还有7分钟时:
若选第一条路线,即X~N(5,1),
能及时到达的概率
P1=P(X≤7)=P(X≤5)+P(5
能及时到达的概率
P2=P(X≤7)=P(X≤6)+P(6
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为P1
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.在某市的高三质量检测考试中,数学成绩服从正态分布N(98,100).已知参加本次考试的全市学生约有9 450人,如果某学生在这次考试中的数学成绩是108分,那么他的数学成绩大约排在全市第
A.1 498名 B.1 700名 C.4 500名 D.8 000名
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.一批电阻的电阻值X(单位:Ω)服从正态分布N(1 000,52),现从甲、乙两箱出厂的成品中各随机抽取一个电阻,测得电阻值分别为1 011 Ω和982 Ω,可以认为
A.甲、乙两箱电阻均可出厂
B.甲、乙两箱电阻均不可出厂
C.甲箱电阻可出厂,乙箱电阻不可出厂
D.甲箱电阻不可出厂,乙箱电阻可出厂
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵X~N(1 000,52),∴μ=1 000,σ=5,
∴μ-3σ=1 000-3×5=985,
μ+3σ=1 000+3×5=1 015.
∵1 011∈(985,1 015),982 (985,1 015),
∴甲箱电阻可出厂,乙箱电阻不可出厂.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.某工厂生产一种螺栓,在正常情况下,螺栓的直径X(单位:mm)服从正态分布X~N(100,1).现加工10个螺栓的尺寸(单位:mm)如下:101.7,100.3,99.6,102.4,98.2,103.2,101.1,98.8,100.4,100.0.X~N(μ,σ2),有P(μ-2σ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知随机变量X~N(2,22),且aX+b(a>0)服从标准正态分布N(0,1),则
a=____,b=____.
-1
解析 ∵随机变量X~N(2,22),
∴E(X)=2,D(X)=22=4.
∴E(aX+b)=aE(X)+b=2a+b=0,
D(aX+b)=a2D(X)=4a2=1,
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.P(Y≥μ2)≥P(Y≥μ1)
B.P(X≤σ2)≤P(X≤σ1)
C.对任意正数t,P(X≤t)>P(Y≤t)
D.对任意正数t,P(X>t)>P(Y>t)
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题图可知μ1<0<μ2,σ1<σ2,
∴P(Y≥μ2)
当t为任意正数时,由题图可知P(X≤t)>P(Y≤t),
而P(X≤t)=1-P(X>t),P(Y≤t)=1-P(Y>t),
∴P(X>t)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某高校为了解全校学生的阅读情况,随机调查了200名学生每周阅读时间X(单位:小时)并绘制如图所示的频率分布直方图.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
s2=(6-9)2×0.03+(7-9)2×0.1+(8-9)2×0.2+(9-9)2×0.35+(10-9)2×0.19+(11-9)2×0.09+(12-9)2×0.04=1.78.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由(1)知μ=9,σ2=1.78,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②从该高校的学生中随机抽取20名,记Z表示这20名学生中每周阅读时间超过10小时的人数,求P(Z≥2)(结果精确到0.000 1)以及Z的均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由①知P(X>10)=1-P(X≤10)=0.226 6,
可得Z~B(20,0.226 6),
P(Z≥2)=1-P(Z=0)-P(Z=1)
=1-(0.773 4+20×0.226 6)×0.007 6
≈0.959 7.
∴Z的均值E(Z)=20×0.226 6=4.532.
本课结束
