高中数学苏教版(2022春 )选择性必修第二册 第8章 习题课 二项分布、超几何分布、正态分布(82张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 第8章 习题课 二项分布、超几何分布、正态分布(82张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览











文档简介
(共82张PPT)
习题课 二项分布、超几何分布、正态分布
第8章 概 率
进一步掌握二项分布、超几何分布、正态分布.
学习目标
随堂演练
课时对点练
一、二项分布及应用
二、超几何分布及应用
内容索引
三、正态分布与二项分布的综合应用
一、二项分布及应用
例1 甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团,游戏规则为:
①先将一个圆8等分(如图),再将8个等分点A1,A2,
A3,A4,A5,A6,A7,A8分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球,然后用摸出的两个小球上标注的分点与圆心O构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球.
(1)求甲能参加音乐社团的概率;
其中与圆心O构成直角三角形的取法有8种:A1A3O,A2A4O,A3A5O,A4A6O,A5A7O,A6A8O,A7A1O,A8A2O,与圆心O构成钝角三角形的取法有8种:A1A4O,A2A5O,A3A6O,A4A7O,A5A8O,A6A1O,A7A2O,A8A3O.
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量X,求X的概率分布、均值和方差.
解 由题意可知,
所以X的概率分布为
反思感悟 与二项分布有关的问题关键是二项分布的判定,可从以下几个方面判定
(1)每次试验中,事件发生的概率是相同的且各事件是相互独立的.
(2)每次试验只有两种结果:发生或不发生.
(3)随机变量是这n重伯努利试验中某事件发生的次数.
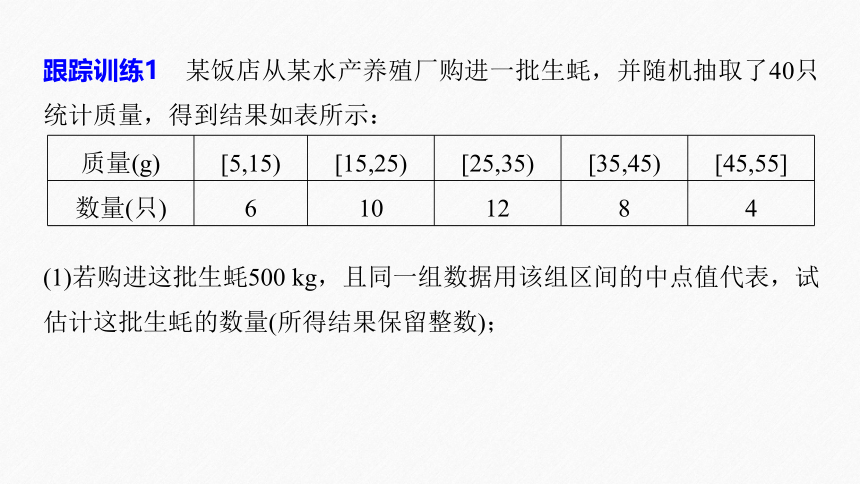
跟踪训练1 某饭店从某水产养殖厂购进一批生蚝,并随机抽取了40只统计质量,得到结果如表所示:
质量(g) [5,15) [15,25) [25,35) [35,45) [45,55]
数量(只) 6 10 12 8 4
(1)若购进这批生蚝500 kg,且同一组数据用该组区间的中点值代表,试估计这批生蚝的数量(所得结果保留整数);
解 由表格中的数据可估算出这批生蚝质量的平均数为
所以购进生蚝500 kg,
(2)以频率视为概率,若在本次购买的生蚝中随机挑选4个,记质量在[5,25)间的生蚝的个数为X,求X的概率分布及均值.
解 由表格中的数据可知,任意挑选一只,
随机变量X的可能取值有0,1,2,3,4,
所以随机变量X的概率分布为
二、超几何分布及应用
例2 某超市在节日期间进行有奖促销,凡在该超市购物满500元的顾客,可以获得一次抽奖机会,有两种方案.方案一:在抽奖的盒子中有除颜色外完全相同的2个黑球,3个白球,顾客一次性摸出2个球,规定摸到2个黑球奖励50元,1个黑球奖励20元,没有摸到黑球奖励15元.方案二:在抽奖的盒子中有除颜色外完全相同的2个黑球,3个白球,顾客不放回地每次摸出一个球,直到将所有黑球摸出则停止摸球,规定2次摸出所有黑球奖励50元,3次摸出所有黑球奖励30元,4次摸出所有黑球奖励20元,5次摸出所有黑球奖励10元.
(1)记X为1名顾客选择方案一时摸出黑球的个数,求随机变量X的均值;
解 方法一 易知X服从超几何分布,且N=5,M=2,n=2,
方法二 X的所有可能取值为0,1,2.
(2)若你是1名要抽奖的顾客,你会选择哪种方案进行抽奖?并说明理由.
解 记Y为1名顾客选择方案一进行抽奖获得的奖金数额,则Y可取50,20,15.
记Z为1名顾客选择方案二进行抽奖获得的奖金数额,
则Z可取50,30,20,10.
E(Y)>E(Z),
∴我会选择方案一进行抽奖.
反思感悟 超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.
跟踪训练2 为了适当疏导电价矛盾,保障电力供应,支持可再生能源发展,促进节能减排,某省于2018年推出了省内居民阶梯电价的计算标准:以一个年度为计费周期、月度滚动使用,第一阶梯电量:年用电量2 160度以下(含2 160度),执行第一档电价0.565 3元/度;第二阶梯电量:年用电量2 161至4 200度(含4 200度),执行第二档电价0.615 3元/度;第三阶梯电量:年用电量4 200度以上,执行第三档电价0.865 3元/度.某市的电力部门从本市的用电户中随机抽取10户,统计其同一年度的用电情况,如表所示:
用户 编号 1 2 3 4 5 6 7 8 9 10
年用 电量 (度) 1 000 1 260 1 400 1 824 2 180 2 423 2 815 3 325 4 411 4 600
(1)试计算表中编号为10的用电户本年度应交电费多少元?
解 因为第二档电价比第一档电价多0.05元/度,第三档电价比第一档电价多0.3元/度,编号为10的用电户一年的用电量是4 600度,则该户本年度应交电费为4 600×0.565 3+(4 200-2 160)×0.05+(4 600-4 200)×0.3=2 822.38(元).
(2)现要在这10户家庭中任意选取4户,对其用电情况作进一步分析,求取到第二阶梯电量的户数的概率分布.
解 设取到第二阶梯电量的用户数为X,可知第二阶梯电量的用户有4户,则X的可能取值为0,1,2,3,4.
故X的概率分布为
三、正态分布与二项分布的综合应用
例3 九所学校参加联考,参加人数约5 000,经计算得数学平均分为113分.已知本次联考的成绩服从正态分布,且标准差为12.
(1)计算联考成绩在137分以上的人数.(结果保留整数)
解 设本次联考成绩为ξ,
由题意知ξ~N(μ,σ2),其中σ=12,μ=113.
因为137=μ+2σ,
故所求人数为0.023×5 000=115.
(2)从所有试卷中任意抽取1份,已知成绩不超过123分的概率为0.8.
①求成绩低于103分的概率.
解 P(ξ<103)=P(ξ>123)=1-0.8=0.2.
②从所有试卷中任意抽取5份,由于试卷数量较大,可以把每份试卷被抽到的概率视为相同,X表示抽到成绩低于103分的试卷的份数,写出X的概率分布,并求出均值E(X).
参考数据:若X~N(μ,σ2),则P(μ-σ解 由题意可知X~B(5,0.2),
故P(X=0)=0.85=0.327 68,
P(X=5)=0.25=0.000 32.
所以X的概率分布为
X 0 1 2 3 4 5
P 0.327 68 0.409 6 0.204 8 0.051 2 0.006 4 0.000 32
E(X)=5×0.2=1.
反思感悟 (1)利用正态分布的概率公式求得满足条件的概率,再乘以总人数,可得结果.
(2)利用正态分布的对称性求概率.
跟踪训练3 “过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数 (同一组中的数据用该组区间的中点值作代表);
解 根据频率分布直方图可得各组的频率为
(0,10]的频率为0.010×10=0.1,
(10,20]的频率为0.020×10=0.2,
(20,30]的频率为0.030×10=0.3,
(30,40]的频率为0.025×10=0.25,
(40,50]的频率为0.015×10=0.15,
(2)①由直方图可以认为,速冻水饺的该项质量指标值Z服从正态分布N(μ,σ2),利用该正态分布,求Z落在(38.45,50.4)内的概率;
②若Z~N(μ,σ2),则P(μ-σ解 ∵Z服从正态分布N(μ,σ2),且μ=26.5,σ≈11.95,
P(38.45=(0.954-0.683)÷2=0.135 5,
∴Z落在(38.45,50.4)内的概率是0.135 5.
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于(10,30)内的包数为X,求X的概率分布和均值及方差.
②若Z~N(μ,σ2),则P(μ-σ解 根据题意得每包速冻水饺的质量指标值位于(10,30)内的概率为0.2+0.3=0.5,
X的可能取值为0,1,2,3,4,
∴X的概率分布为
1.知识清单:二项分布、超几何分布、正态分布.
2.方法归纳:转化化归、数形结合.
3.常见误区:注意区分超几何分布和二项分布.
课堂小结
随堂演练
1.某一供电网络有n个用电单位,每个单位在一天中用电的机会都是p,则供电网络中一天平均用电的单位个数是
A.np(1-p) B.np
C.n D.p(1-p)
1
2
3
4
解析 用电单位的个数X~B(n,p),∴E(X)=np.
√
1
2
3
4
2.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如表所示:
使用时 间/天 10~20 21~30 31~40 41~50 51~60
个数 10 40 80 50 20
若以频率为概率,现从该批次机械元件中随机抽取3个,则至少有2个元件的使用寿命在30天以上的概率为
√
1
2
3
4
使用时 间/天 10~20 21~30 31~40 41~50 51~60
个数 10 40 80 50 20
1
2
3
4
3.已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.15,则P(2≤ξ<4)等于
A.0.3 B.0.35 C.0.5 D.0.7
√
解析 ∵P(ξ<2)=P(ξ>6)=0.15,
又P(2≤ξ≤6)=1-P(ξ<2)-P(ξ>6)=0.7,
4.在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用X表示这10个村庄中交通不方便的村庄数,则P(X=4)=________.(用数字表示)
1
2
3
4
课时对点练
基础巩固
1.若X~B(5,0.1),则P(X≤2)等于
A.0.665 B.0.008 56
C.0.918 54 D.0.991 44
√
解析 P(X≤2)=P(X=0)+P(X=1)+P(X=2)
=0.991 44.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知随机变量X的概率分布为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.有8名学生,其中有5名男生,从中选出4名代表,选出的代表中男生人数为X,则其均值E(X)等于
A.2 B.2.5 C.3 D.3.5
√
解析 由题意可知X服从超几何分布,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于A,P(X=1)=E(X),故A正确;
故B正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.一批产品共50件,其中5件次品,其余均为合格品,从这批产品中任意抽取两件,其中出现次品的概率为______.
解析 设抽取的两件产品中次品的件数为X,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知某种从太空飞船中带回来的植被种子每粒成功发芽的概率都为 ,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,如果某次没有发芽,则称该次试验是失败的.
(1)第一小组做了3次试验,记该小组试验成功的次数为X,求X的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意,得随机变量X的可能取值为0,1,2,3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)第二小组进行试验,到成功了4次为止,求在第4次成功之前共有3次失败的概率.
解 第二小组第7次试验成功,前面6次试验中有3次失败,3次成功,每次试验又是相互独立的,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.袋中有4只红球,3只黑球,今从袋中随机取出4只球,设取到一只红球得2分,取得一只黑球得1分,试求得分X的均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 取出4只球颜色及得分情况是
4红得8分,3红1黑得7分,2红2黑得6分,1红3黑得5分,因此,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.设随机变量ξ~N(μ,1),函数f(x)=x2+2x-ξ没有零点的概率是0.5,则P(0<ξ≤1)等于
附:若ξ~N(μ,σ2),则P(μ-σP(μ-2σA.0.158 7 B.0.135 5
C.0.271 8 D.0.341 3
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵函数f(x)=x2+2x-ξ没有零点,
∴二次方程x2+2x-ξ=0无实根,
∴Δ=4-4(-ξ)<0,∴ξ<-1,
又∵f(x)=x2+2x-ξ没有零点的概率是0.5,
∴P(ξ<-1)=0.5,
由正态曲线的对称性知μ=-1,
∴ξ~N(-1,1),∴μ=-1,σ=1,
∴μ-σ=-2,μ+σ=0,μ-2σ=-3,μ+2σ=1,
∴P(-2<ξ<0)=0.683,P(-3<ξ<1)=0.954,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
∴n(10-n)(9-n)(8-n)=480,将选项中的值代入检验,知选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.“石头、剪刀、布”又称“猜丁壳”,是一种流行多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在语音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”,而“布”又胜过“石头”.若所出的拳相同,则为和局.小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小军和大明比赛至第四局小军胜出的概率是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 根据“石头”胜“剪刀”、“剪刀”胜“布”,而“布”又胜“石头”,可得每局比赛中小军胜大明、小军与大明和局和小军输给大明的概率都为 ,
∴小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,比赛至第四局小军胜出,指前3局中小军胜2局,有1局不胜,第四局小军胜,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.3月5日为“学雷锋纪念日”,某校将举行“弘扬雷锋精神做全面发展一代新人”知识竞赛,某班现从6名女生和3名男生中选出5名学生参赛,要求每人回答一个问题,答对得2分,答错得0分,已知6名女生中有2人不会答所有题目,只能得0分,其余4人可得2分,3名男生每人得2分的概率均为 ,现选择2名女生和3名男生,每人答一题,则该班所
选队员得分之和为6分的概率为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 依题意设该班所选队员得分之和为6分记为事件A,
则可分为下列三类:女生得0分男生得6分,设为事件A1;女生得2分男生得4分,设为事件A2;女生得4分男生得2分,设为事件A3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某市举办数学知识竞赛活动,共5 000名学生参加,竞赛分为初试和复试,复试环节共3道题,其中2道单选题,1道多选题,得分规则如下:参赛学生每答对一道单选题得2分,答错得0分,答对多选题得3分,答错得0分,答完3道题后的得分之和为参赛学生的复试成绩.
(1)通过分析可以认为学生初试成绩X服从正态分布N(μ,σ2),其中μ=66,σ2=144,试估计初试成绩超过90分的人数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 ∵学生初试成绩X服从正态分布N(μ,σ2),
其中μ=66,σ2=144,
∴μ+2σ=66+2×12=90,
∴P(X>90)=P(X>μ+2σ)
∴估计初试成绩超过90分的人数为0.023×5 000=115.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
附:P(μ-σ1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 Y的所有可能取值为0,2,3,4,5,7,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴Y的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
习题课 二项分布、超几何分布、正态分布
第8章 概 率
进一步掌握二项分布、超几何分布、正态分布.
学习目标
随堂演练
课时对点练
一、二项分布及应用
二、超几何分布及应用
内容索引
三、正态分布与二项分布的综合应用
一、二项分布及应用
例1 甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团,游戏规则为:
①先将一个圆8等分(如图),再将8个等分点A1,A2,
A3,A4,A5,A6,A7,A8分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球,然后用摸出的两个小球上标注的分点与圆心O构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球.
(1)求甲能参加音乐社团的概率;
其中与圆心O构成直角三角形的取法有8种:A1A3O,A2A4O,A3A5O,A4A6O,A5A7O,A6A8O,A7A1O,A8A2O,与圆心O构成钝角三角形的取法有8种:A1A4O,A2A5O,A3A6O,A4A7O,A5A8O,A6A1O,A7A2O,A8A3O.
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量X,求X的概率分布、均值和方差.
解 由题意可知,
所以X的概率分布为
反思感悟 与二项分布有关的问题关键是二项分布的判定,可从以下几个方面判定
(1)每次试验中,事件发生的概率是相同的且各事件是相互独立的.
(2)每次试验只有两种结果:发生或不发生.
(3)随机变量是这n重伯努利试验中某事件发生的次数.
跟踪训练1 某饭店从某水产养殖厂购进一批生蚝,并随机抽取了40只统计质量,得到结果如表所示:
质量(g) [5,15) [15,25) [25,35) [35,45) [45,55]
数量(只) 6 10 12 8 4
(1)若购进这批生蚝500 kg,且同一组数据用该组区间的中点值代表,试估计这批生蚝的数量(所得结果保留整数);
解 由表格中的数据可估算出这批生蚝质量的平均数为
所以购进生蚝500 kg,
(2)以频率视为概率,若在本次购买的生蚝中随机挑选4个,记质量在[5,25)间的生蚝的个数为X,求X的概率分布及均值.
解 由表格中的数据可知,任意挑选一只,
随机变量X的可能取值有0,1,2,3,4,
所以随机变量X的概率分布为
二、超几何分布及应用
例2 某超市在节日期间进行有奖促销,凡在该超市购物满500元的顾客,可以获得一次抽奖机会,有两种方案.方案一:在抽奖的盒子中有除颜色外完全相同的2个黑球,3个白球,顾客一次性摸出2个球,规定摸到2个黑球奖励50元,1个黑球奖励20元,没有摸到黑球奖励15元.方案二:在抽奖的盒子中有除颜色外完全相同的2个黑球,3个白球,顾客不放回地每次摸出一个球,直到将所有黑球摸出则停止摸球,规定2次摸出所有黑球奖励50元,3次摸出所有黑球奖励30元,4次摸出所有黑球奖励20元,5次摸出所有黑球奖励10元.
(1)记X为1名顾客选择方案一时摸出黑球的个数,求随机变量X的均值;
解 方法一 易知X服从超几何分布,且N=5,M=2,n=2,
方法二 X的所有可能取值为0,1,2.
(2)若你是1名要抽奖的顾客,你会选择哪种方案进行抽奖?并说明理由.
解 记Y为1名顾客选择方案一进行抽奖获得的奖金数额,则Y可取50,20,15.
记Z为1名顾客选择方案二进行抽奖获得的奖金数额,
则Z可取50,30,20,10.
E(Y)>E(Z),
∴我会选择方案一进行抽奖.
反思感悟 超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.
跟踪训练2 为了适当疏导电价矛盾,保障电力供应,支持可再生能源发展,促进节能减排,某省于2018年推出了省内居民阶梯电价的计算标准:以一个年度为计费周期、月度滚动使用,第一阶梯电量:年用电量2 160度以下(含2 160度),执行第一档电价0.565 3元/度;第二阶梯电量:年用电量2 161至4 200度(含4 200度),执行第二档电价0.615 3元/度;第三阶梯电量:年用电量4 200度以上,执行第三档电价0.865 3元/度.某市的电力部门从本市的用电户中随机抽取10户,统计其同一年度的用电情况,如表所示:
用户 编号 1 2 3 4 5 6 7 8 9 10
年用 电量 (度) 1 000 1 260 1 400 1 824 2 180 2 423 2 815 3 325 4 411 4 600
(1)试计算表中编号为10的用电户本年度应交电费多少元?
解 因为第二档电价比第一档电价多0.05元/度,第三档电价比第一档电价多0.3元/度,编号为10的用电户一年的用电量是4 600度,则该户本年度应交电费为4 600×0.565 3+(4 200-2 160)×0.05+(4 600-4 200)×0.3=2 822.38(元).
(2)现要在这10户家庭中任意选取4户,对其用电情况作进一步分析,求取到第二阶梯电量的户数的概率分布.
解 设取到第二阶梯电量的用户数为X,可知第二阶梯电量的用户有4户,则X的可能取值为0,1,2,3,4.
故X的概率分布为
三、正态分布与二项分布的综合应用
例3 九所学校参加联考,参加人数约5 000,经计算得数学平均分为113分.已知本次联考的成绩服从正态分布,且标准差为12.
(1)计算联考成绩在137分以上的人数.(结果保留整数)
解 设本次联考成绩为ξ,
由题意知ξ~N(μ,σ2),其中σ=12,μ=113.
因为137=μ+2σ,
故所求人数为0.023×5 000=115.
(2)从所有试卷中任意抽取1份,已知成绩不超过123分的概率为0.8.
①求成绩低于103分的概率.
解 P(ξ<103)=P(ξ>123)=1-0.8=0.2.
②从所有试卷中任意抽取5份,由于试卷数量较大,可以把每份试卷被抽到的概率视为相同,X表示抽到成绩低于103分的试卷的份数,写出X的概率分布,并求出均值E(X).
参考数据:若X~N(μ,σ2),则P(μ-σ
故P(X=0)=0.85=0.327 68,
P(X=5)=0.25=0.000 32.
所以X的概率分布为
X 0 1 2 3 4 5
P 0.327 68 0.409 6 0.204 8 0.051 2 0.006 4 0.000 32
E(X)=5×0.2=1.
反思感悟 (1)利用正态分布的概率公式求得满足条件的概率,再乘以总人数,可得结果.
(2)利用正态分布的对称性求概率.
跟踪训练3 “过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数 (同一组中的数据用该组区间的中点值作代表);
解 根据频率分布直方图可得各组的频率为
(0,10]的频率为0.010×10=0.1,
(10,20]的频率为0.020×10=0.2,
(20,30]的频率为0.030×10=0.3,
(30,40]的频率为0.025×10=0.25,
(40,50]的频率为0.015×10=0.15,
(2)①由直方图可以认为,速冻水饺的该项质量指标值Z服从正态分布N(μ,σ2),利用该正态分布,求Z落在(38.45,50.4)内的概率;
②若Z~N(μ,σ2),则P(μ-σ
P(38.45
∴Z落在(38.45,50.4)内的概率是0.135 5.
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于(10,30)内的包数为X,求X的概率分布和均值及方差.
②若Z~N(μ,σ2),则P(μ-σ
X的可能取值为0,1,2,3,4,
∴X的概率分布为
1.知识清单:二项分布、超几何分布、正态分布.
2.方法归纳:转化化归、数形结合.
3.常见误区:注意区分超几何分布和二项分布.
课堂小结
随堂演练
1.某一供电网络有n个用电单位,每个单位在一天中用电的机会都是p,则供电网络中一天平均用电的单位个数是
A.np(1-p) B.np
C.n D.p(1-p)
1
2
3
4
解析 用电单位的个数X~B(n,p),∴E(X)=np.
√
1
2
3
4
2.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如表所示:
使用时 间/天 10~20 21~30 31~40 41~50 51~60
个数 10 40 80 50 20
若以频率为概率,现从该批次机械元件中随机抽取3个,则至少有2个元件的使用寿命在30天以上的概率为
√
1
2
3
4
使用时 间/天 10~20 21~30 31~40 41~50 51~60
个数 10 40 80 50 20
1
2
3
4
3.已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.15,则P(2≤ξ<4)等于
A.0.3 B.0.35 C.0.5 D.0.7
√
解析 ∵P(ξ<2)=P(ξ>6)=0.15,
又P(2≤ξ≤6)=1-P(ξ<2)-P(ξ>6)=0.7,
4.在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用X表示这10个村庄中交通不方便的村庄数,则P(X=4)=________.(用数字表示)
1
2
3
4
课时对点练
基础巩固
1.若X~B(5,0.1),则P(X≤2)等于
A.0.665 B.0.008 56
C.0.918 54 D.0.991 44
√
解析 P(X≤2)=P(X=0)+P(X=1)+P(X=2)
=0.991 44.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知随机变量X的概率分布为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.有8名学生,其中有5名男生,从中选出4名代表,选出的代表中男生人数为X,则其均值E(X)等于
A.2 B.2.5 C.3 D.3.5
√
解析 由题意可知X服从超几何分布,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于A,P(X=1)=E(X),故A正确;
故B正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.一批产品共50件,其中5件次品,其余均为合格品,从这批产品中任意抽取两件,其中出现次品的概率为______.
解析 设抽取的两件产品中次品的件数为X,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知某种从太空飞船中带回来的植被种子每粒成功发芽的概率都为 ,某植物研究所分两个小组分别独立开展该种子的发芽试验,每次试验种一粒种子,如果某次没有发芽,则称该次试验是失败的.
(1)第一小组做了3次试验,记该小组试验成功的次数为X,求X的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意,得随机变量X的可能取值为0,1,2,3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)第二小组进行试验,到成功了4次为止,求在第4次成功之前共有3次失败的概率.
解 第二小组第7次试验成功,前面6次试验中有3次失败,3次成功,每次试验又是相互独立的,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.袋中有4只红球,3只黑球,今从袋中随机取出4只球,设取到一只红球得2分,取得一只黑球得1分,试求得分X的均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 取出4只球颜色及得分情况是
4红得8分,3红1黑得7分,2红2黑得6分,1红3黑得5分,因此,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.设随机变量ξ~N(μ,1),函数f(x)=x2+2x-ξ没有零点的概率是0.5,则P(0<ξ≤1)等于
附:若ξ~N(μ,σ2),则P(μ-σ
C.0.271 8 D.0.341 3
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵函数f(x)=x2+2x-ξ没有零点,
∴二次方程x2+2x-ξ=0无实根,
∴Δ=4-4(-ξ)<0,∴ξ<-1,
又∵f(x)=x2+2x-ξ没有零点的概率是0.5,
∴P(ξ<-1)=0.5,
由正态曲线的对称性知μ=-1,
∴ξ~N(-1,1),∴μ=-1,σ=1,
∴μ-σ=-2,μ+σ=0,μ-2σ=-3,μ+2σ=1,
∴P(-2<ξ<0)=0.683,P(-3<ξ<1)=0.954,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
∴n(10-n)(9-n)(8-n)=480,将选项中的值代入检验,知选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.“石头、剪刀、布”又称“猜丁壳”,是一种流行多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在语音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”,而“布”又胜过“石头”.若所出的拳相同,则为和局.小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小军和大明比赛至第四局小军胜出的概率是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 根据“石头”胜“剪刀”、“剪刀”胜“布”,而“布”又胜“石头”,可得每局比赛中小军胜大明、小军与大明和局和小军输给大明的概率都为 ,
∴小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,比赛至第四局小军胜出,指前3局中小军胜2局,有1局不胜,第四局小军胜,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.3月5日为“学雷锋纪念日”,某校将举行“弘扬雷锋精神做全面发展一代新人”知识竞赛,某班现从6名女生和3名男生中选出5名学生参赛,要求每人回答一个问题,答对得2分,答错得0分,已知6名女生中有2人不会答所有题目,只能得0分,其余4人可得2分,3名男生每人得2分的概率均为 ,现选择2名女生和3名男生,每人答一题,则该班所
选队员得分之和为6分的概率为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 依题意设该班所选队员得分之和为6分记为事件A,
则可分为下列三类:女生得0分男生得6分,设为事件A1;女生得2分男生得4分,设为事件A2;女生得4分男生得2分,设为事件A3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某市举办数学知识竞赛活动,共5 000名学生参加,竞赛分为初试和复试,复试环节共3道题,其中2道单选题,1道多选题,得分规则如下:参赛学生每答对一道单选题得2分,答错得0分,答对多选题得3分,答错得0分,答完3道题后的得分之和为参赛学生的复试成绩.
(1)通过分析可以认为学生初试成绩X服从正态分布N(μ,σ2),其中μ=66,σ2=144,试估计初试成绩超过90分的人数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 ∵学生初试成绩X服从正态分布N(μ,σ2),
其中μ=66,σ2=144,
∴μ+2σ=66+2×12=90,
∴P(X>90)=P(X>μ+2σ)
∴估计初试成绩超过90分的人数为0.023×5 000=115.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
附:P(μ-σ
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 Y的所有可能取值为0,2,3,4,5,7,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴Y的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
