高中数学苏教版(2022春 )选择性必修第二册 第8章 再练一课(范围:§8.1~8.2.2)(31张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 第8章 再练一课(范围:§8.1~8.2.2)(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 11:38:21 | ||
图片预览











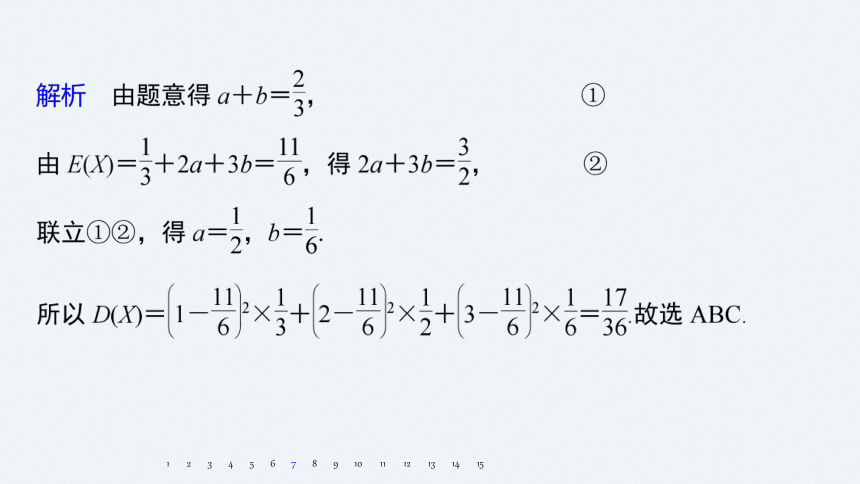
文档简介
(共31张PPT)
第8章 概 率
再练一课(范围:§8.1~8.2.2)
1.某班学生考试成绩中,数学不及格的占15%,语文不及格的占5%,两门都不及格的占3%.已知一学生数学不及格,则他语文也不及格的概率是
A.0.2 B.0.33 C.0.5 D.0.6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
一、单项选择题
√
所以数学不及格时,该生语文也不及格的概率为0.2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
解析 ∵随机变量ξ的分布列为
3.设随机变量ξ等可能地取1,2,3,4,…,10,又设随机变量η=2ξ-1,则P(η<6)等于
A.0.3 B.0.5 C.0.1 D.0.2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
解析 因为随机变量ξ等可能地取1,2,3,4,…,10,
所以η=2ξ-1等可能的取1,3,5,7,…,19,
所以P(η<6)=P(η=1)+P(η=3)+P(η=5)=0.3.
4.已知随机变量X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X 0 1
P 1-p p
√
解析 由题意得E(X)=0×(1-p)+1×p=p,
则D(X)=(0-p)2·(1-p)+(1-p)2·p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5.如图展现给我们的是唐代著名诗人杜牧写的《清明》,这首诗不仅意境极好,而且还准确地描述出了清明时节的天气状况,那就是“雨纷纷”,即天气多阴雨.某地区气象监测资料表明,清明节当天下雨的概率是0.9,连续两天下雨的概率是0.63,若该地某年清明节当天下雨,则随后一天也下雨的概率是
A.0.63 B.0.7
C.0.9 D.0.567
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 记事件A表示“清明节当天下雨”,事件B表示“第二天下雨”,
由题意可知,P(A)=0.9,P(AB)=0.63,
6.甲、乙两台自动车床生产同种标准件,X表示甲车床生产1 000件产品中的次品数,Y表示乙车床生产1 000件产品中的次品数,经一段时间考察,X,Y的概率分布分别是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X 0 1 2 3
P 0.7 0.1 0.1 0.1
Y 0 1 2 3
P 0.5 0.3 0.2 0
据此判定
A.甲比乙质量好 B.乙比甲质量好
C.甲与乙质量相同 D.无法判定
√
解析 E(X)=0×0.7+1×0.1+2×0.1+3×0.1=0.6,
E(Y)=0×0.5+1×0.3+2×0.2+3×0=0.7.
由于E(Y)>E(X),
故甲比乙质量好.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7.已知随机变量X的概率分布是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
二、多项选择题
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8.有3台车床加工同一型号的零件.第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床的零件数分别占总数的25%,30%,45%,则下列选项正确的有
A.任取一个零件是第1台生产出来的次品概率为0.06
B.任取一个零件是次品的概率为0.052 5
C.如果取到的零件是次品,且是第2台车床加工的概率为
D.如果取到的零件是次品,且是第3台车床加工的概率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
√
解析 记Ai为事件“零件为第i(i=1,2,3)台车床加工”,记B为事件“任取一个零件为次品”,
则P(A1)=0.25,P(A2)=0.3,P(A3)=0.45,
对于A,即P(A1B)=P(A1)·P(B|A1)=0.25×0.06=0.015,A错误.
对于B,P(B)=P(A1)·P(B|A1)+P(A2)·P(B|A2)+P(A3)·P(B|A3)=0.25×0.06+0.3×0.05+0.45×0.05=0.052 5,B正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
三、填空题
解析 记事件A表示“第一次取到的是130分以上试卷”,事件B表示“第二次取到的是90分以下试卷”.
事件A发生所包含的样本点数n(A)=3×4=12,
9.桌子上放有5张学生的期中考试数学卷,有3张在130分以上,2张在90分以下,老师为了准确了解学生情况,每次任取一张,不放回地取两次,若第一次取到130分以上的一张,则第二次取到90分以下的一张试卷的概率为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10.已知A1,A2为两所高校举行的强基计划考试,某同学参加每所高校的考试获得通过的概率均为 ,该同学一旦通过一所高校的考试,就不再参加另一所高校的考试,设该同学通过高校考试的个数为随机变量X,则D(X)=____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 X的所有可能的取值为0,1,
11.如图,将一个各面都涂了油漆的正方体切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X,
则X的均值为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 根据题意易知X=0,1,2,3,概率分布如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12.从1~100共100个正整数中任取一数,已知取出的一个数不大于50,
则此数是2或3的倍数的概率为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
四、解答题
13.春节期间,小王用私家车送4位朋友到三个旅游景点去游玩,每位朋友在每一个景点下车的概率均为 ,用ξ表示4位朋友在第三个景点下车的人数,求:
(1)随机变量ξ的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 ξ的所有可能值为0,1,2,3,4.
从而ξ的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)随机变量ξ的均值.
解 由(1)得ξ的均值为
14.设甲盒有3个白球,2个红球,乙盒有4个白球,1个红球,现从甲盒任取2个球放入乙盒,再从乙盒任取2个球,
(1)求从乙盒取出2个红球的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 设A1=“从甲盒取出2个红球”;
A2=“从甲盒取出2个白球”;
A3=“从甲盒取出1个白球1个红球”;
B=“从乙盒取出2个红球”.
则A1,A2,A3两两互斥,且A1+A2+A3=Ω,所以
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)已知从乙盒取出2个红球,求从甲盒取出2个红球的概率.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15.随机抽取某厂的某种产品200件,经质检,其中一等品126件,二等品50件,三等品20件,次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为X.
(1)求X的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 X的所有可能取值有6,2,1,-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
故X的概率分布为
X 6 2 1 -2
P 0.63 0.25 0.1 0.02
(2)求1件产品的平均利润(即X的均值);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 E(X)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34.
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 设技术革新后的三等品率为x,
则此时1件产品的平均利润为
E(X)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29).
依题意知,E(X)≥4.73,即4.76-x≥4.73,
解得x≤0.03,所以三等品率最多为3%.
本课结束
第8章 概 率
再练一课(范围:§8.1~8.2.2)
1.某班学生考试成绩中,数学不及格的占15%,语文不及格的占5%,两门都不及格的占3%.已知一学生数学不及格,则他语文也不及格的概率是
A.0.2 B.0.33 C.0.5 D.0.6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
一、单项选择题
√
所以数学不及格时,该生语文也不及格的概率为0.2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
解析 ∵随机变量ξ的分布列为
3.设随机变量ξ等可能地取1,2,3,4,…,10,又设随机变量η=2ξ-1,则P(η<6)等于
A.0.3 B.0.5 C.0.1 D.0.2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
解析 因为随机变量ξ等可能地取1,2,3,4,…,10,
所以η=2ξ-1等可能的取1,3,5,7,…,19,
所以P(η<6)=P(η=1)+P(η=3)+P(η=5)=0.3.
4.已知随机变量X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X 0 1
P 1-p p
√
解析 由题意得E(X)=0×(1-p)+1×p=p,
则D(X)=(0-p)2·(1-p)+(1-p)2·p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5.如图展现给我们的是唐代著名诗人杜牧写的《清明》,这首诗不仅意境极好,而且还准确地描述出了清明时节的天气状况,那就是“雨纷纷”,即天气多阴雨.某地区气象监测资料表明,清明节当天下雨的概率是0.9,连续两天下雨的概率是0.63,若该地某年清明节当天下雨,则随后一天也下雨的概率是
A.0.63 B.0.7
C.0.9 D.0.567
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 记事件A表示“清明节当天下雨”,事件B表示“第二天下雨”,
由题意可知,P(A)=0.9,P(AB)=0.63,
6.甲、乙两台自动车床生产同种标准件,X表示甲车床生产1 000件产品中的次品数,Y表示乙车床生产1 000件产品中的次品数,经一段时间考察,X,Y的概率分布分别是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X 0 1 2 3
P 0.7 0.1 0.1 0.1
Y 0 1 2 3
P 0.5 0.3 0.2 0
据此判定
A.甲比乙质量好 B.乙比甲质量好
C.甲与乙质量相同 D.无法判定
√
解析 E(X)=0×0.7+1×0.1+2×0.1+3×0.1=0.6,
E(Y)=0×0.5+1×0.3+2×0.2+3×0=0.7.
由于E(Y)>E(X),
故甲比乙质量好.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7.已知随机变量X的概率分布是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
二、多项选择题
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8.有3台车床加工同一型号的零件.第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床的零件数分别占总数的25%,30%,45%,则下列选项正确的有
A.任取一个零件是第1台生产出来的次品概率为0.06
B.任取一个零件是次品的概率为0.052 5
C.如果取到的零件是次品,且是第2台车床加工的概率为
D.如果取到的零件是次品,且是第3台车床加工的概率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
√
解析 记Ai为事件“零件为第i(i=1,2,3)台车床加工”,记B为事件“任取一个零件为次品”,
则P(A1)=0.25,P(A2)=0.3,P(A3)=0.45,
对于A,即P(A1B)=P(A1)·P(B|A1)=0.25×0.06=0.015,A错误.
对于B,P(B)=P(A1)·P(B|A1)+P(A2)·P(B|A2)+P(A3)·P(B|A3)=0.25×0.06+0.3×0.05+0.45×0.05=0.052 5,B正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
三、填空题
解析 记事件A表示“第一次取到的是130分以上试卷”,事件B表示“第二次取到的是90分以下试卷”.
事件A发生所包含的样本点数n(A)=3×4=12,
9.桌子上放有5张学生的期中考试数学卷,有3张在130分以上,2张在90分以下,老师为了准确了解学生情况,每次任取一张,不放回地取两次,若第一次取到130分以上的一张,则第二次取到90分以下的一张试卷的概率为___.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10.已知A1,A2为两所高校举行的强基计划考试,某同学参加每所高校的考试获得通过的概率均为 ,该同学一旦通过一所高校的考试,就不再参加另一所高校的考试,设该同学通过高校考试的个数为随机变量X,则D(X)=____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 X的所有可能的取值为0,1,
11.如图,将一个各面都涂了油漆的正方体切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X,
则X的均值为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 根据题意易知X=0,1,2,3,概率分布如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12.从1~100共100个正整数中任取一数,已知取出的一个数不大于50,
则此数是2或3的倍数的概率为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
四、解答题
13.春节期间,小王用私家车送4位朋友到三个旅游景点去游玩,每位朋友在每一个景点下车的概率均为 ,用ξ表示4位朋友在第三个景点下车的人数,求:
(1)随机变量ξ的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 ξ的所有可能值为0,1,2,3,4.
从而ξ的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)随机变量ξ的均值.
解 由(1)得ξ的均值为
14.设甲盒有3个白球,2个红球,乙盒有4个白球,1个红球,现从甲盒任取2个球放入乙盒,再从乙盒任取2个球,
(1)求从乙盒取出2个红球的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 设A1=“从甲盒取出2个红球”;
A2=“从甲盒取出2个白球”;
A3=“从甲盒取出1个白球1个红球”;
B=“从乙盒取出2个红球”.
则A1,A2,A3两两互斥,且A1+A2+A3=Ω,所以
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)已知从乙盒取出2个红球,求从甲盒取出2个红球的概率.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15.随机抽取某厂的某种产品200件,经质检,其中一等品126件,二等品50件,三等品20件,次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为X.
(1)求X的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 X的所有可能取值有6,2,1,-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
故X的概率分布为
X 6 2 1 -2
P 0.63 0.25 0.1 0.02
(2)求1件产品的平均利润(即X的均值);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 E(X)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34.
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解 设技术革新后的三等品率为x,
则此时1件产品的平均利润为
E(X)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29).
依题意知,E(X)≥4.73,即4.76-x≥4.73,
解得x≤0.03,所以三等品率最多为3%.
本课结束
