高中数学苏教版(2022春 )选择性必修第二册 8.1.2 全概率公式-8.1.3 贝叶斯公式(65张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 8.1.2 全概率公式-8.1.3 贝叶斯公式(65张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 11:52:53 | ||
图片预览










文档简介
(共65张PPT)
8.1.2 全概率公式
8.1.3 贝叶斯公式*
第8章 § 8.1 条件概率
1.结合古典概型,理解并掌握全概率公式,会利用全概率公式计
算概率.
2.了解贝叶斯公式(不作考试要求).
学习目标
狼来了这个故事大家都听过,那么从心理学角度分析,这个小孩是如何一步步丧失村民信任的呢?我们可以通过特殊概率公式来解读.
设A为事件“小孩说谎”,B为“村民觉得小孩可信”;不妨设可信的小孩说谎的概率为0.1,而不可信的小孩说谎的概率为0.5,经过第一次撒谎,第二次撒谎后,狼真的来了,小孩第三次呼救的时候,村民都不再相信这是真的,觉得这是谁家熊孩子真气人,没人再上山救他.于是,狼在前两次跳出来吓唬完小孩就跑走后,成功在第三次抓走小孩,而且无人打扰,由此可见心理学结合概率统计学很重要!
导语
随堂演练
课时对点练
一、全概率公式
二、多个事件的全概率问题
三、贝叶斯公式*
内容索引
一、全概率公式
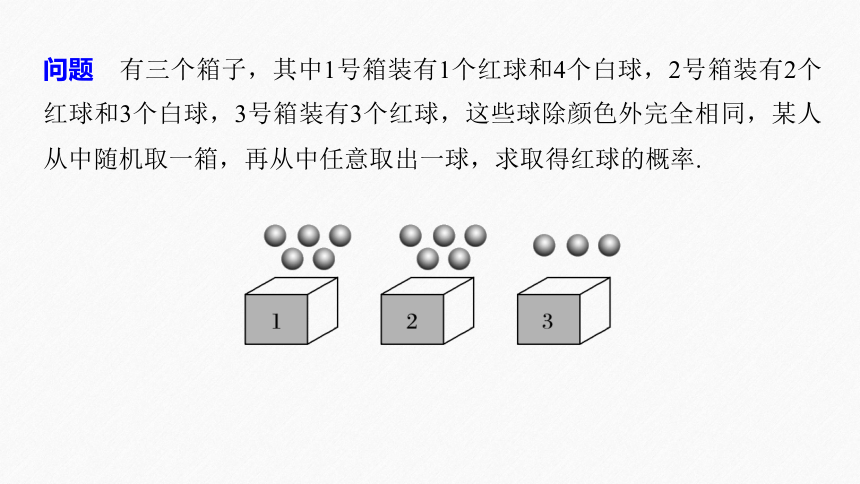
问题 有三个箱子,其中1号箱装有1个红球和4个白球,2号箱装有2个红球和3个白球,3号箱装有3个红球,这些球除颜色外完全相同,某人从中随机取一箱,再从中任意取出一球,求取得红球的概率.
提示 设事件Bi表示“球取自i号箱”(i=1,2,3),事件A表示“取得红球”,其中B1,B2,B3两两互斥,A发生总是伴随着B1,B2,B3之一同时发生,即A=B1A∪B2A∪B3A,且B1A,B2A,B3A两两互斥,运用互斥事件概率的加法公式得到P(A)=P(B1A)+P(B2A)+P(B3A),再对求和中的每一项运用乘法公式得
知识梳理
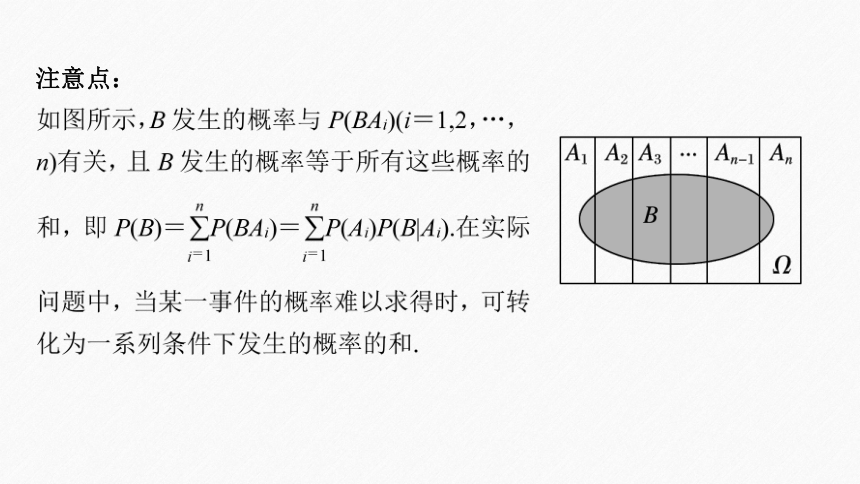
一般地,若事件A1,A2,…,An两两 ,且它们的和 = ,P(Ai)>0,i=1,2,…,n,则对于Ω中的任意事件B,有P(B)=
.这个公式称为全概率公式(total probability formula).
互斥
Ω
注意点:
解 如果用事件A1,A2分别表示“居民所遇到的一位同学是甲班的与乙班的”,事件B表示“居民所遇到的一位同学是女生”,则Ω=A1∪A2,且A1,A2互斥,B Ω,
反思感悟 两个事件的全概率问题求解策略
(2)计算:利用乘法公式计算每一部分的概率.
(3)求和:所求事件的概率P(B)=P(A1)P(B|A1)+P(A2)P(B|A2).
跟踪训练1 某商店收进甲厂生产的产品30箱,乙厂生产的同种产品20箱,甲厂每箱装100个,废品率为0.06,乙厂每箱装120个,废品率为0.05,求:
(1)任取一箱,从中任取一个为废品的概率;
解 记事件A,B分别为“甲、乙两厂的产品”,事件C为“废品”,
则Ω=A∪B,且A,B互斥,
P(C|A)=0.06,P(C|B)=0.05,由全概率公式,
(2)若将所有产品开箱混放,求任取一个为废品的概率.
P(C|A)=0.06,P(C|B)=0.05,
二、多个事件的全概率问题
例2 某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录有如下表所示的数据:
元件制造厂 次品率 提供元件的份额
1 0.02 0.15
2 0.01 0.80
3 0.03 0.05
设这三家元件制造厂的元件在仓库中是均匀混合的,且无区别的标志.在仓库中随机地取一只元件,求它是次品的概率.
解 设事件Bi表示所取到的产品是由第i家元件制造厂提供的(i=1,2,3),事件A表示取到的是一件次品.
其中B1,B2,B3两两互斥,A发生总是伴随着B1,B2,B3之一发生,
即A=B1A∪B2A∪B3A,且B1A,B2A,B3A两两互斥,
运用互斥事件概率的加法公式和乘法公式,得
P(A)=P(B1A)+P(B2A)+P(B3A)
=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)(A|B3)
=0.15×0.02+0.80×0.01+0.05×0.03
=0.012 5.
因此,在仓库中随机地取一只元件,它是次品的概率为0.012 5.
延伸探究 假设某工厂生产的甲、乙、丙三种产品的百分率和三种产品的优质率的信息如下表所示:
产品种类 甲 乙 丙
百分率 60% 20% 20%
优质率 90% 85% 80%
在生产的产品中任取一件,求取到的产品是优质品的概率.
解 用A1,A2,A3表示甲、乙、丙产品,B表示优质品,
由已知得P(A1)=60%,P(A2)=20%,P(A3)=20%,
且P(B|A1)=90%,P(B|A2)=85%,P(B|A3)=80%.
因此由全概率公式有P(B)=P(A1)P(B|A1)+P(A2)·P(B|A2)+P(A3)P(B|A3)=60%×90%+20%×85%+20%×80%=54%+17%+16%=87%.
反思感悟 “化整为零”求多事件的全概率问题
(2)已知事件B的发生有各种可能的情形Ai(i=1,2,…,n),事件B发生的可能性,就是各种可能情形Ai发生的可能性与已知在Ai发生的条件下事件B发生的可能性的乘积之和.
跟踪训练2 甲箱的产品中有5个正品和3个次品,乙箱的产品中有4个正品和3个次品.
(1)从甲箱中任取2个产品,求这2个产品都是次品的概率;
(2)若从甲箱中任取2个产品放入乙箱中,然后再从乙箱中任取一个产品,求取出的这个产品是正品的概率.
解 设事件A为“从乙箱中取出的一个产品是正品”,事件B1为“从甲箱中取出2个产品都是正品”,事件B2为“从甲箱中取出1个正品1个次品”,事件B3为“从甲箱中取出2个产品都是次品”,则事件B1、事件B2、事件B3彼此互斥.
三、贝叶斯公式*
知识梳理
(2)P(A1)称为先验概率,P(A1|B)称为后验概率,其反映了事情A1发生的可能在各种可能原因中的比重.
例3 小张从家到公司上班总共有三条路可以走(如图),但是每条路每天拥堵的可能性不太一样,由于远近不同,选择每条路的概率分别为P(L1)=0.5,P(L2)=0.3,P(L3)=0.2,每天上述三条路不拥堵的概率分别为P(C1)=0.2,P(C2)=0.4,P(C3)=0.7.假设遇到拥堵会迟到,那么:
(1)小张从家到公司不迟到的概率是多少?
解 由题意知,不迟到就意味着不拥堵,设事件C表示到公司不迟到,则
P(C)=P(L1)×P(C|L1)+P(L2)×P(C|L2)+P(L3)×P(C|L3)
=P(L1)×P(C1)+P(L2)×P(C2)+P(L3)×P(C3)
=0.5×0.2+0.3×0.4+0.2×0.7=0.36.
(2)已知到达公司未迟到,选择道路L1的概率是多少?
所以已知到达公司未迟到,选择道路L1的概率约为0.28.
反思感悟 若随机试验可以看成分两个阶段进行,且第一阶段的各试验结果具体结果怎样未知,那么:(1)如果要求的是第二阶段某一个结果发生的概率,则用全概率公式;(2)如果第二个阶段的某一个结果是已知的,要求的是此结果为第一阶段某一个结果所引起的概率,一般用贝叶斯公式,类似于求条件概率,熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确、高效.
跟踪训练3 设某公路上经过的货车与客车的数量之比为2∶1,货车中途停车修理的概率为0.02,客车为0.01,今有一辆汽车中途停车修理,求该汽车是货车的概率.
解 设B表示事件“中途停车修理”,A1表示事件“经过的是货车”,A2表示事件“经过的是客车”,
则B=A1B∪A2B,由贝叶斯公式得
1.知识清单:
(1)全概率公式.
(2)贝叶斯公式.
2.方法归纳:化整为零、转化化归.
3.常见误区:事件拆分不合理或不全面.
课堂小结
随堂演练
1
2
3
4
A.0.08 B.0.8 C.0.6 D.0.5
√
解析 因为P(BA)=P(A)P(B|A),
1
2
3
4
2.有朋自远方来,乘火车、船、汽车、飞机来的概率分别为0.3,0.2,0.1,0.4,迟到的概率分别为0.25,0.3,0.1,0,则他迟到的概率为
A.0.65 B.0.075 C.0.145 D.0
解析 设A1表示事件“他乘火车来”,A2表示事件“他乘船来”,A3表示事件“他乘汽车来”,A4表示事件“他乘飞机来”,B表示事件“他迟到”.
√
=0.3×0.25+0.2×0.3+0.1×0.1+0.4×0=0.145.
1
2
3
4
3.盒中有a个红球,b个黑球,今随机地从中取出一个,观察其颜色后放回,并加上同色球c个,再从盒中抽取一球,则第二次抽出的是黑球的概率是
√
1
2
3
4
1
2
3
4
4.一项血液化验用来鉴别是否患有某种疾病,在患有此种疾病的人群中通过化验有95%的人呈阳性反应,而健康的人通过化验也会有1%的人呈阳性反应,某地区此种病患者占人口数的0.5%,则:
(1)某人化验结果为阳性的概率为________;
1.47%
解析 A=“呈阳性反应”,B=“患有此种病”.
P(A)=0.5%×95%+99.5%×1%=1.47%.
1
2
3
4
(2)若此人化验结果为阳性,则此人确实患有此病的概率为________.
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.甲、乙、丙三个车间生产同一种产品,其产量分别占总量的25%,35%,40%,次品率分别为5%,4%,2%.从这批产品中任取一件,则它是次品的概率为
A.0.012 3 B.0.023 4 C.0.034 5 D.0.045 6
√
解析 所求概率为0.25×0.05+0.35×0.04+0.4×0.02=0.034 5.
2.已知5%的男人和0.25%的女人患色盲,假如男人、女人各占一半,现随机选一人,则此人恰是色盲的概率是
A.0.012 45 B.0.057 86
C.0.026 25 D.0.028 65
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.两台机床加工同样的零件,第一台的废品率为0.04,第二台的废品率为0.07,加工出来的零件混放,并设第一台加工的零件是第二台加工零件的2倍,现任取一零件,则它是合格品的概率为
A.0.21 B.0.06 C.0.94 D.0.95
解析 令B=“取到的零件为合格品”,Ai=“零件为第i台机床的产品”,i=1,2.由全概率公式得
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.0.08 B.0.1 C.0.15 D.0.2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则由全概率公式,得所求概率为P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.一袋中装有10个球,其中3个黑球、7个白球,从中先后随意各取一球(不放回),则第二次取到的是黑球的概率为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.设有来自三个地区的各10名、15名和25名考生的报名表,其中女生报名表分别为3份、7份和5份,随机地取一个地区的报名表,从中先后取出两份,则先取到的一份为女生表的概率为
√
解析 设A表示事件“先取到的是女生表”,Bi表示事件“取到第i个地区的表”,i=1,2,3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.人们为了解一支股票未来一定时期内价格的变化,往往会去分析影响股票价格的基本因素,比如利率的变化.现假设人们经分析估计利率下调的概率为60%,利率不变的概率为40%.根据经验,人们估计,在利率下调的情况下,该支股票价格上涨的概率为80%,而在利率不变的情况下,其价格上涨的概率为40%,则该支股票将上涨的概率为_____.
64%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.袋中装有编号为1,2,…,N的N个球,先从袋中任取一球,如该球不是1号球就放回袋中,是1号球就不放回,然后再摸一次,则取到2号球
的概率为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问:
(1)从1号箱中取出的是红球的条件下,从2号箱取出红球的概率是多少?
解 记事件A:最后从2号箱中取出的是红球;
事件B:从1号箱中取出的是红球.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)从2号箱取出红球的概率是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设Ai=“第i个地区”,i=1,2,3;B=“感染此病”,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若此人感染此病,求此人来自乙地区的概率.
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.把外形相同的球分装在三个盒子中,每盒10个.其中,第一个盒子中有7个球标有字母A,3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中有红球8个,白球2个.试验按如下规则进行:先在第一个盒子中任取一个球,若取得标有字母A的球,则在第二个盒子中任取一个球;若第一次取得标有字母B的球,则在第三个盒子中任取一个球.如果第二次取出的是红球,则称试验成功,则试验成功的概率为
A.0.59 B.0.41 C.0.48 D.0.64
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设A表示事件“从第一个盒子中取得标有字母A的球”,
B表示事件“从第一个盒子中取得标有字母B的球”,
R表示事件“第二次取出的球是红球”,
P(R)=P(R|A)P(A)+P(R|B)P(B)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设袋中有12个球,9个新球,3个旧球,第一次比赛取3球并使用,比赛后放回,第二次比赛再任取3球,则第二次比赛取得3个新球的概率为
解析 设Ai=“第一次比赛恰取出i个新球(i=0,1,2,3)”,B=“第二次比赛取得3个新球”,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设A=收到“·”,B=发出“·”,
由贝叶斯公式得
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若n∈N,n≥2,用Pn-1表示Pn的表达式为_________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.同一种产品由甲、乙、丙三个厂供应.由长期的经验知,三家的正品率分别为0.95,0.90,0.80,三家产品数所占比例为2∶3∶5,混合在一起.
(1)从中任取一件,求此产品为正品的概率;
解 设事件A表示取到的产品为正品,B1,B2,B3分别表示产品由甲、乙、丙厂生产.则Ω=B1∪B2∪B3,且B1,B2,B3两两互斥,
由已知P(B1)=0.2,P(B2)=0.3,P(B3)=0.5,
P(A|B1)=0.95,P(A|B2)=0.9,P(A|B3)=0.8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)现取到一件产品为正品,问它是由甲、乙、丙三个厂中哪个厂生产的可能性大?
解 由贝叶斯公式得
由以上3个数作比较,可知这件产品由丙厂生产的可能性最大,由甲厂生产的可能性最小.
本课结束
8.1.2 全概率公式
8.1.3 贝叶斯公式*
第8章 § 8.1 条件概率
1.结合古典概型,理解并掌握全概率公式,会利用全概率公式计
算概率.
2.了解贝叶斯公式(不作考试要求).
学习目标
狼来了这个故事大家都听过,那么从心理学角度分析,这个小孩是如何一步步丧失村民信任的呢?我们可以通过特殊概率公式来解读.
设A为事件“小孩说谎”,B为“村民觉得小孩可信”;不妨设可信的小孩说谎的概率为0.1,而不可信的小孩说谎的概率为0.5,经过第一次撒谎,第二次撒谎后,狼真的来了,小孩第三次呼救的时候,村民都不再相信这是真的,觉得这是谁家熊孩子真气人,没人再上山救他.于是,狼在前两次跳出来吓唬完小孩就跑走后,成功在第三次抓走小孩,而且无人打扰,由此可见心理学结合概率统计学很重要!
导语
随堂演练
课时对点练
一、全概率公式
二、多个事件的全概率问题
三、贝叶斯公式*
内容索引
一、全概率公式
问题 有三个箱子,其中1号箱装有1个红球和4个白球,2号箱装有2个红球和3个白球,3号箱装有3个红球,这些球除颜色外完全相同,某人从中随机取一箱,再从中任意取出一球,求取得红球的概率.
提示 设事件Bi表示“球取自i号箱”(i=1,2,3),事件A表示“取得红球”,其中B1,B2,B3两两互斥,A发生总是伴随着B1,B2,B3之一同时发生,即A=B1A∪B2A∪B3A,且B1A,B2A,B3A两两互斥,运用互斥事件概率的加法公式得到P(A)=P(B1A)+P(B2A)+P(B3A),再对求和中的每一项运用乘法公式得
知识梳理
一般地,若事件A1,A2,…,An两两 ,且它们的和 = ,P(Ai)>0,i=1,2,…,n,则对于Ω中的任意事件B,有P(B)=
.这个公式称为全概率公式(total probability formula).
互斥
Ω
注意点:
解 如果用事件A1,A2分别表示“居民所遇到的一位同学是甲班的与乙班的”,事件B表示“居民所遇到的一位同学是女生”,则Ω=A1∪A2,且A1,A2互斥,B Ω,
反思感悟 两个事件的全概率问题求解策略
(2)计算:利用乘法公式计算每一部分的概率.
(3)求和:所求事件的概率P(B)=P(A1)P(B|A1)+P(A2)P(B|A2).
跟踪训练1 某商店收进甲厂生产的产品30箱,乙厂生产的同种产品20箱,甲厂每箱装100个,废品率为0.06,乙厂每箱装120个,废品率为0.05,求:
(1)任取一箱,从中任取一个为废品的概率;
解 记事件A,B分别为“甲、乙两厂的产品”,事件C为“废品”,
则Ω=A∪B,且A,B互斥,
P(C|A)=0.06,P(C|B)=0.05,由全概率公式,
(2)若将所有产品开箱混放,求任取一个为废品的概率.
P(C|A)=0.06,P(C|B)=0.05,
二、多个事件的全概率问题
例2 某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录有如下表所示的数据:
元件制造厂 次品率 提供元件的份额
1 0.02 0.15
2 0.01 0.80
3 0.03 0.05
设这三家元件制造厂的元件在仓库中是均匀混合的,且无区别的标志.在仓库中随机地取一只元件,求它是次品的概率.
解 设事件Bi表示所取到的产品是由第i家元件制造厂提供的(i=1,2,3),事件A表示取到的是一件次品.
其中B1,B2,B3两两互斥,A发生总是伴随着B1,B2,B3之一发生,
即A=B1A∪B2A∪B3A,且B1A,B2A,B3A两两互斥,
运用互斥事件概率的加法公式和乘法公式,得
P(A)=P(B1A)+P(B2A)+P(B3A)
=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)(A|B3)
=0.15×0.02+0.80×0.01+0.05×0.03
=0.012 5.
因此,在仓库中随机地取一只元件,它是次品的概率为0.012 5.
延伸探究 假设某工厂生产的甲、乙、丙三种产品的百分率和三种产品的优质率的信息如下表所示:
产品种类 甲 乙 丙
百分率 60% 20% 20%
优质率 90% 85% 80%
在生产的产品中任取一件,求取到的产品是优质品的概率.
解 用A1,A2,A3表示甲、乙、丙产品,B表示优质品,
由已知得P(A1)=60%,P(A2)=20%,P(A3)=20%,
且P(B|A1)=90%,P(B|A2)=85%,P(B|A3)=80%.
因此由全概率公式有P(B)=P(A1)P(B|A1)+P(A2)·P(B|A2)+P(A3)P(B|A3)=60%×90%+20%×85%+20%×80%=54%+17%+16%=87%.
反思感悟 “化整为零”求多事件的全概率问题
(2)已知事件B的发生有各种可能的情形Ai(i=1,2,…,n),事件B发生的可能性,就是各种可能情形Ai发生的可能性与已知在Ai发生的条件下事件B发生的可能性的乘积之和.
跟踪训练2 甲箱的产品中有5个正品和3个次品,乙箱的产品中有4个正品和3个次品.
(1)从甲箱中任取2个产品,求这2个产品都是次品的概率;
(2)若从甲箱中任取2个产品放入乙箱中,然后再从乙箱中任取一个产品,求取出的这个产品是正品的概率.
解 设事件A为“从乙箱中取出的一个产品是正品”,事件B1为“从甲箱中取出2个产品都是正品”,事件B2为“从甲箱中取出1个正品1个次品”,事件B3为“从甲箱中取出2个产品都是次品”,则事件B1、事件B2、事件B3彼此互斥.
三、贝叶斯公式*
知识梳理
(2)P(A1)称为先验概率,P(A1|B)称为后验概率,其反映了事情A1发生的可能在各种可能原因中的比重.
例3 小张从家到公司上班总共有三条路可以走(如图),但是每条路每天拥堵的可能性不太一样,由于远近不同,选择每条路的概率分别为P(L1)=0.5,P(L2)=0.3,P(L3)=0.2,每天上述三条路不拥堵的概率分别为P(C1)=0.2,P(C2)=0.4,P(C3)=0.7.假设遇到拥堵会迟到,那么:
(1)小张从家到公司不迟到的概率是多少?
解 由题意知,不迟到就意味着不拥堵,设事件C表示到公司不迟到,则
P(C)=P(L1)×P(C|L1)+P(L2)×P(C|L2)+P(L3)×P(C|L3)
=P(L1)×P(C1)+P(L2)×P(C2)+P(L3)×P(C3)
=0.5×0.2+0.3×0.4+0.2×0.7=0.36.
(2)已知到达公司未迟到,选择道路L1的概率是多少?
所以已知到达公司未迟到,选择道路L1的概率约为0.28.
反思感悟 若随机试验可以看成分两个阶段进行,且第一阶段的各试验结果具体结果怎样未知,那么:(1)如果要求的是第二阶段某一个结果发生的概率,则用全概率公式;(2)如果第二个阶段的某一个结果是已知的,要求的是此结果为第一阶段某一个结果所引起的概率,一般用贝叶斯公式,类似于求条件概率,熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确、高效.
跟踪训练3 设某公路上经过的货车与客车的数量之比为2∶1,货车中途停车修理的概率为0.02,客车为0.01,今有一辆汽车中途停车修理,求该汽车是货车的概率.
解 设B表示事件“中途停车修理”,A1表示事件“经过的是货车”,A2表示事件“经过的是客车”,
则B=A1B∪A2B,由贝叶斯公式得
1.知识清单:
(1)全概率公式.
(2)贝叶斯公式.
2.方法归纳:化整为零、转化化归.
3.常见误区:事件拆分不合理或不全面.
课堂小结
随堂演练
1
2
3
4
A.0.08 B.0.8 C.0.6 D.0.5
√
解析 因为P(BA)=P(A)P(B|A),
1
2
3
4
2.有朋自远方来,乘火车、船、汽车、飞机来的概率分别为0.3,0.2,0.1,0.4,迟到的概率分别为0.25,0.3,0.1,0,则他迟到的概率为
A.0.65 B.0.075 C.0.145 D.0
解析 设A1表示事件“他乘火车来”,A2表示事件“他乘船来”,A3表示事件“他乘汽车来”,A4表示事件“他乘飞机来”,B表示事件“他迟到”.
√
=0.3×0.25+0.2×0.3+0.1×0.1+0.4×0=0.145.
1
2
3
4
3.盒中有a个红球,b个黑球,今随机地从中取出一个,观察其颜色后放回,并加上同色球c个,再从盒中抽取一球,则第二次抽出的是黑球的概率是
√
1
2
3
4
1
2
3
4
4.一项血液化验用来鉴别是否患有某种疾病,在患有此种疾病的人群中通过化验有95%的人呈阳性反应,而健康的人通过化验也会有1%的人呈阳性反应,某地区此种病患者占人口数的0.5%,则:
(1)某人化验结果为阳性的概率为________;
1.47%
解析 A=“呈阳性反应”,B=“患有此种病”.
P(A)=0.5%×95%+99.5%×1%=1.47%.
1
2
3
4
(2)若此人化验结果为阳性,则此人确实患有此病的概率为________.
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.甲、乙、丙三个车间生产同一种产品,其产量分别占总量的25%,35%,40%,次品率分别为5%,4%,2%.从这批产品中任取一件,则它是次品的概率为
A.0.012 3 B.0.023 4 C.0.034 5 D.0.045 6
√
解析 所求概率为0.25×0.05+0.35×0.04+0.4×0.02=0.034 5.
2.已知5%的男人和0.25%的女人患色盲,假如男人、女人各占一半,现随机选一人,则此人恰是色盲的概率是
A.0.012 45 B.0.057 86
C.0.026 25 D.0.028 65
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.两台机床加工同样的零件,第一台的废品率为0.04,第二台的废品率为0.07,加工出来的零件混放,并设第一台加工的零件是第二台加工零件的2倍,现任取一零件,则它是合格品的概率为
A.0.21 B.0.06 C.0.94 D.0.95
解析 令B=“取到的零件为合格品”,Ai=“零件为第i台机床的产品”,i=1,2.由全概率公式得
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.0.08 B.0.1 C.0.15 D.0.2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则由全概率公式,得所求概率为P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.一袋中装有10个球,其中3个黑球、7个白球,从中先后随意各取一球(不放回),则第二次取到的是黑球的概率为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.设有来自三个地区的各10名、15名和25名考生的报名表,其中女生报名表分别为3份、7份和5份,随机地取一个地区的报名表,从中先后取出两份,则先取到的一份为女生表的概率为
√
解析 设A表示事件“先取到的是女生表”,Bi表示事件“取到第i个地区的表”,i=1,2,3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.人们为了解一支股票未来一定时期内价格的变化,往往会去分析影响股票价格的基本因素,比如利率的变化.现假设人们经分析估计利率下调的概率为60%,利率不变的概率为40%.根据经验,人们估计,在利率下调的情况下,该支股票价格上涨的概率为80%,而在利率不变的情况下,其价格上涨的概率为40%,则该支股票将上涨的概率为_____.
64%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.袋中装有编号为1,2,…,N的N个球,先从袋中任取一球,如该球不是1号球就放回袋中,是1号球就不放回,然后再摸一次,则取到2号球
的概率为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问:
(1)从1号箱中取出的是红球的条件下,从2号箱取出红球的概率是多少?
解 记事件A:最后从2号箱中取出的是红球;
事件B:从1号箱中取出的是红球.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)从2号箱取出红球的概率是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设Ai=“第i个地区”,i=1,2,3;B=“感染此病”,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若此人感染此病,求此人来自乙地区的概率.
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.把外形相同的球分装在三个盒子中,每盒10个.其中,第一个盒子中有7个球标有字母A,3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中有红球8个,白球2个.试验按如下规则进行:先在第一个盒子中任取一个球,若取得标有字母A的球,则在第二个盒子中任取一个球;若第一次取得标有字母B的球,则在第三个盒子中任取一个球.如果第二次取出的是红球,则称试验成功,则试验成功的概率为
A.0.59 B.0.41 C.0.48 D.0.64
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设A表示事件“从第一个盒子中取得标有字母A的球”,
B表示事件“从第一个盒子中取得标有字母B的球”,
R表示事件“第二次取出的球是红球”,
P(R)=P(R|A)P(A)+P(R|B)P(B)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设袋中有12个球,9个新球,3个旧球,第一次比赛取3球并使用,比赛后放回,第二次比赛再任取3球,则第二次比赛取得3个新球的概率为
解析 设Ai=“第一次比赛恰取出i个新球(i=0,1,2,3)”,B=“第二次比赛取得3个新球”,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设A=收到“·”,B=发出“·”,
由贝叶斯公式得
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若n∈N,n≥2,用Pn-1表示Pn的表达式为_________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.同一种产品由甲、乙、丙三个厂供应.由长期的经验知,三家的正品率分别为0.95,0.90,0.80,三家产品数所占比例为2∶3∶5,混合在一起.
(1)从中任取一件,求此产品为正品的概率;
解 设事件A表示取到的产品为正品,B1,B2,B3分别表示产品由甲、乙、丙厂生产.则Ω=B1∪B2∪B3,且B1,B2,B3两两互斥,
由已知P(B1)=0.2,P(B2)=0.3,P(B3)=0.5,
P(A|B1)=0.95,P(A|B2)=0.9,P(A|B3)=0.8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)现取到一件产品为正品,问它是由甲、乙、丙三个厂中哪个厂生产的可能性大?
解 由贝叶斯公式得
由以上3个数作比较,可知这件产品由丙厂生产的可能性最大,由甲厂生产的可能性最小.
本课结束
