高中数学苏教版(2022春 )选择性必修第二册 8.2.3 第2课时 二项分布的综合问题(85张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 8.2.3 第2课时 二项分布的综合问题(85张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 11:40:41 | ||
图片预览











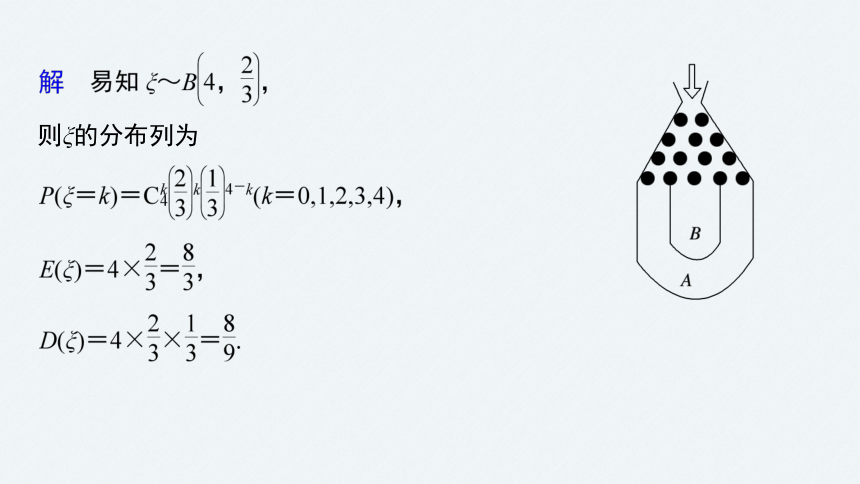
文档简介
(共85张PPT)
第2课时 二项分布的综合问题
第8章 8.2.3 二项分布
1.掌握二项分布的均值与方差公式.
2.能利用二项分布解决一些简单的实际问题.
学习目标
姚明作为中锋,他职业生涯的罚球命中率为0.8,假设他每次命中率相同,请问他5投4中的概率是多少?
导语
随堂演练
课时对点练
一、二项分布的均值与方差
二、二项分布的实际应用
三、二项分布的性质
内容索引
一、二项分布的均值与方差
问题 若随机变量X服从二项分布B(n,p),那么X的均值和方差各是什么?
提示 当n=1时,X服从两点分布,分布列为
X 0 1
P 1-p p
E(X)=p,D(X)=p(1-p).
二项分布的分布列为(q=1-p)
=np(p+q)n-1=np,
同理可得D(X)=np(1-p).
知识梳理
1.若X服从两点分布,则E(X)= ,D(X)= .
p
p(1-p)
2.若X~B(n,p),则E(X)= ,D(X)= ,σ= .
np
np(1-p)
例1 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,在下落的过程中,小球将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 .
(1)分别求出小球落入A袋和B袋中的概率;
解 设M=“小球落入A袋”,N=“小球落入B袋”,
(2)在容器的入口处依次放入4个小球,记ξ为落入B袋中的小球的个数,求ξ的分布列、均值和方差.
则ξ的分布列为
反思感悟 解决此类问题第一步是判断随机变量X服从什么分布,第二步代入相应的公式求解.若X服从两点分布,则E(X)=p,D(X)=p(1-p);若X服从二项分布,即X~B(n,p),则E(X)=np,D(X)=np(1-p).
跟踪训练1 某一智力游戏玩一次所得的积分是一个随机变量X,其分布列如下表,均值E(X)=2.
(1)求a和b的值;
解 因为E(X)=2,
(2)某同学连续玩三次该智力游戏,记积分X大于0的次数为Y,求Y的概率分布与均值.
X 0 3 6
P a b
故Y的概率分布为
二、二项分布的实际应用
例2 为了了解校园噪音情况,学校环保协会对校园环境噪音值(单位:分贝)进行了50天的监测,得到如下统计表:
环境噪音值 (单位:分贝) [55, 57] (57, 59] (59, 61] (61, 63] (63, 65] (65,
67]
频数 1 4 12 20 8 5
(1)根据该统计表,求这50天校园噪音值的样本平均数(同一组的数据用该组的组中值作代表);
解 由数据可知样本平均数为
=61.8(分贝).
(2)若环境噪音值超过65分贝,视为重度噪音污染,环境噪音值不超过59分贝,视为轻度噪音污染,把由上述统计表算得的频率视作概率,回答下列问题:
①求周一到周五的5天中恰有两天校园出现重度噪音污染而其余3天都是轻度噪音污染的概率;
设事件A为“周一至周五的5天中恰有两天校园出现重度噪音污染而其余3天都是轻度噪音污染”,
②学校要举行为期3天的“汉字听写大赛”校园选拔赛,把这3天校园出现的重度噪音污染天数记为X,求X的分布列和方差D(X).
则随机变量X的分布列为
所以D(X)=np(1-p)=0.27.
反思感悟 二项分布的实际应用类问题的求解步骤
(1)根据题意设出随机变量;
(2)分析随机变量服从二项分布;
(3)求出参数n和p的值;
(4)根据二项分布的均值、方差的计算公式求解.
跟踪训练2 一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是 .
(1)求这名学生在途中遇到红灯的次数ξ的均值;
故ξ的概率分布为
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的概率分布;
解 这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的取值为0,1,2,3,4,5.
故η的概率分布为
(3)求这名学生在途中至少遇到一次红灯的概率.
解 所求概率为P(ξ≥1)=1-P(ξ=0)
三、二项分布的性质
例3 某一批产品的合格率为95%,那么在取出的20件产品中,最有可能有几件产品合格?
则当k<19.95时,P(X=k-1)当k>19.95时,P(X=k-1)>P(X=k),
由以上分析可知,在取出的20件产品中,合格品有19件的概率最大,即最有可能有19件合格品.
反思感悟 二项分布概率最大问题的求解思路
跟踪训练3 若X~B ,则P(X=k)(0≤k≤20且k∈N)取得最大值时,k=______.
6或7
解析 由题意知,X服从二项分布,
解得k≥6.
所以当k≥6时,P(X=k)≥P(X=k+1);
当k<6时,P(X=k+1)>P(X=k).
因为当且仅当k=6时,P(X=k+1)=P(X=k),
所以当k=6或k=7时,P(X=k)取得最大值.
1.知识清单:
(1)二项分布的均值、方差.
(2)二项分布的性质.
2.方法归纳:公式法.
3.常见误区:判断随机变量X是否服从二项分布.
课堂小结
随堂演练
1
2
3
4
1.(多选)下列关于随机变量及分布的说法正确的是
A.抛掷均匀硬币一次,出现正面的次数是随机变量
B.某人射击时命中的概率为0.5,此人射击三次命中的次数X服从两点分布
C.离散型随机变量的分布列中,随机变量取各个值的概率之和可以小于1
D.离散型随机变量的各个可能值表示的事件是彼此互斥的
√
√
1
2
3
4
解析 对于选项A,抛掷均匀硬币一次,出现正面的次数可能是0,也可能是1,故是随机变量,故选项A正确;
对于选项B,某人射击时命中的概率为0.5,此人射击三次是3重伯努利试验,命中的次数X服从二项分布B(3,0.5)而不是两点分布,故选项B错误;
对于选项C,离散型随机变量的分布列中,随机变量取各个值的概率之和一定等于1,故选项C错误;
对于选项D,由互斥事件的定义可知选项D正确.
1
2
3
4
2.同时抛掷两枚质地均匀的硬币10次,设两枚硬币同时出现反面的次数为X,则D(X)等于
√
1
2
3
4
√
1
2
3
4
解析 因为X~B(2,p),
所以P(X≥1)=1-P(X<1)=1-P(X=0)
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.设X~B(40,p),且E(X)=16,则p等于
A.0.1 B.0.2 C.0.3 D.0.4
√
解析 ∵E(X)=16,
∴40p=16,∴p=0.4.
√
所以n=36,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知随机变量X+Y=8,若X~B(10,0.6),则E(Y),D(Y)分别是
A.6和2.4 B.2和2.4
C.2和5.6 D.6和5.6
√
解析 因为X+Y=8,所以Y=8-X.
所以E(Y)=8-E(X)=8-10×0.6=2,
D(Y)=(-1)2D(X)=10×0.6×0.4=2.4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵P(ξ=0)+P(ξ≥1)=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 由二进制数A的特点知每一个数位上的数字只能填0,1,
且每个数位上的数字再填时互不影响,故以后的5位数中后4位的所有结果有4类:
①后4个数出现0,X=0,
②后4个数位只出现1个1,X=1,
③后4个数位出现2个1,X=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
④后4个数位上出现3个1,X=3,
⑤后4个数位都出现1,X=4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.一个病人服用某种新药后被治愈的概率为0.9,则服用这种新药的4个病人中至少3人被治愈的概率为________(用数字作答).
0.947 7
解析 由随机变量X~B(2,p),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求ξ的均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 方法一 ξ的所有可能取值为0,1,2,3,4,
∴ξ的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求n和p的值,并写出X的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意知,X~B(n,p),
由E(X)=np=3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率.
解 记“需要补种沙柳”为事件A,
则P(A)=P(X≤3),
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.袋中有3个白球和i个黑球,有放回的摸取3次,每次摸取一球,设摸得黑球的个数为ξi,其中i=1,2,则
A.E(ξ1)B.E(ξ1)D(ξ2)
C.E(ξ1)>E(ξ2),D(ξ1)D.E(ξ1)>E(ξ2),D(ξ1)>D(ξ2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当i=1时,ξ1可能的取值为0,1,2,3,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当i=2时,ξ2可能的取值为0,1,2,3,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以E(ξ1)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.10 B.20 C.21 D.0
√
解析 由题意知
对比二项展开式得xk+yk=20,
所以符合题意的(xk,yk)有(0,20),(1,19),…,(20,0),共21个.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又k取整数,∴k=13.
拓广探究
15.掷骰子游戏:规定掷出1点,甲盒中放一球,掷出2点或3点,乙盒中放一球,掷出4点、5点或6点,丙盒中放一球,共掷6次,用x,y,z分别表示掷完6次后甲、乙、丙盒中球的个数.令X=x+y,则E(X)=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴E(z)=3,又x+y+z=6,
∴X=x+y=6-z,
∴E(X)=E(6-z)=6-E(z)=6-3=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设A1表示事件“日销售量不低于100个”,A2表示事件“日销售量低于50个”,B表示事件“在未来连续3天里有连续2天的日销售量不低于100个且另1天的日销售量低于50个”.
则P(A1)=(0.006+0.004+0.002)×50=0.6,
P(A2)=0.003×50=0.15,
P(B)=0.6×0.6×0.15×2=0.108.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的概率分布,均值E(X)及方差D(X).
解 X的可能取值为0,1,2,3,相应的概率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则X的概率分布为
X 0 1 2 3
P 0.064 0.288 0.432 0.216
因为X~B(3,0.6),所以均值E(X)=3×0.6=1.8,
方差D(X)=3×0.6×(1-0.6)=0.72.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
第2课时 二项分布的综合问题
第8章 8.2.3 二项分布
1.掌握二项分布的均值与方差公式.
2.能利用二项分布解决一些简单的实际问题.
学习目标
姚明作为中锋,他职业生涯的罚球命中率为0.8,假设他每次命中率相同,请问他5投4中的概率是多少?
导语
随堂演练
课时对点练
一、二项分布的均值与方差
二、二项分布的实际应用
三、二项分布的性质
内容索引
一、二项分布的均值与方差
问题 若随机变量X服从二项分布B(n,p),那么X的均值和方差各是什么?
提示 当n=1时,X服从两点分布,分布列为
X 0 1
P 1-p p
E(X)=p,D(X)=p(1-p).
二项分布的分布列为(q=1-p)
=np(p+q)n-1=np,
同理可得D(X)=np(1-p).
知识梳理
1.若X服从两点分布,则E(X)= ,D(X)= .
p
p(1-p)
2.若X~B(n,p),则E(X)= ,D(X)= ,σ= .
np
np(1-p)
例1 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,在下落的过程中,小球将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 .
(1)分别求出小球落入A袋和B袋中的概率;
解 设M=“小球落入A袋”,N=“小球落入B袋”,
(2)在容器的入口处依次放入4个小球,记ξ为落入B袋中的小球的个数,求ξ的分布列、均值和方差.
则ξ的分布列为
反思感悟 解决此类问题第一步是判断随机变量X服从什么分布,第二步代入相应的公式求解.若X服从两点分布,则E(X)=p,D(X)=p(1-p);若X服从二项分布,即X~B(n,p),则E(X)=np,D(X)=np(1-p).
跟踪训练1 某一智力游戏玩一次所得的积分是一个随机变量X,其分布列如下表,均值E(X)=2.
(1)求a和b的值;
解 因为E(X)=2,
(2)某同学连续玩三次该智力游戏,记积分X大于0的次数为Y,求Y的概率分布与均值.
X 0 3 6
P a b
故Y的概率分布为
二、二项分布的实际应用
例2 为了了解校园噪音情况,学校环保协会对校园环境噪音值(单位:分贝)进行了50天的监测,得到如下统计表:
环境噪音值 (单位:分贝) [55, 57] (57, 59] (59, 61] (61, 63] (63, 65] (65,
67]
频数 1 4 12 20 8 5
(1)根据该统计表,求这50天校园噪音值的样本平均数(同一组的数据用该组的组中值作代表);
解 由数据可知样本平均数为
=61.8(分贝).
(2)若环境噪音值超过65分贝,视为重度噪音污染,环境噪音值不超过59分贝,视为轻度噪音污染,把由上述统计表算得的频率视作概率,回答下列问题:
①求周一到周五的5天中恰有两天校园出现重度噪音污染而其余3天都是轻度噪音污染的概率;
设事件A为“周一至周五的5天中恰有两天校园出现重度噪音污染而其余3天都是轻度噪音污染”,
②学校要举行为期3天的“汉字听写大赛”校园选拔赛,把这3天校园出现的重度噪音污染天数记为X,求X的分布列和方差D(X).
则随机变量X的分布列为
所以D(X)=np(1-p)=0.27.
反思感悟 二项分布的实际应用类问题的求解步骤
(1)根据题意设出随机变量;
(2)分析随机变量服从二项分布;
(3)求出参数n和p的值;
(4)根据二项分布的均值、方差的计算公式求解.
跟踪训练2 一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是 .
(1)求这名学生在途中遇到红灯的次数ξ的均值;
故ξ的概率分布为
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的概率分布;
解 这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的取值为0,1,2,3,4,5.
故η的概率分布为
(3)求这名学生在途中至少遇到一次红灯的概率.
解 所求概率为P(ξ≥1)=1-P(ξ=0)
三、二项分布的性质
例3 某一批产品的合格率为95%,那么在取出的20件产品中,最有可能有几件产品合格?
则当k<19.95时,P(X=k-1)
由以上分析可知,在取出的20件产品中,合格品有19件的概率最大,即最有可能有19件合格品.
反思感悟 二项分布概率最大问题的求解思路
跟踪训练3 若X~B ,则P(X=k)(0≤k≤20且k∈N)取得最大值时,k=______.
6或7
解析 由题意知,X服从二项分布,
解得k≥6.
所以当k≥6时,P(X=k)≥P(X=k+1);
当k<6时,P(X=k+1)>P(X=k).
因为当且仅当k=6时,P(X=k+1)=P(X=k),
所以当k=6或k=7时,P(X=k)取得最大值.
1.知识清单:
(1)二项分布的均值、方差.
(2)二项分布的性质.
2.方法归纳:公式法.
3.常见误区:判断随机变量X是否服从二项分布.
课堂小结
随堂演练
1
2
3
4
1.(多选)下列关于随机变量及分布的说法正确的是
A.抛掷均匀硬币一次,出现正面的次数是随机变量
B.某人射击时命中的概率为0.5,此人射击三次命中的次数X服从两点分布
C.离散型随机变量的分布列中,随机变量取各个值的概率之和可以小于1
D.离散型随机变量的各个可能值表示的事件是彼此互斥的
√
√
1
2
3
4
解析 对于选项A,抛掷均匀硬币一次,出现正面的次数可能是0,也可能是1,故是随机变量,故选项A正确;
对于选项B,某人射击时命中的概率为0.5,此人射击三次是3重伯努利试验,命中的次数X服从二项分布B(3,0.5)而不是两点分布,故选项B错误;
对于选项C,离散型随机变量的分布列中,随机变量取各个值的概率之和一定等于1,故选项C错误;
对于选项D,由互斥事件的定义可知选项D正确.
1
2
3
4
2.同时抛掷两枚质地均匀的硬币10次,设两枚硬币同时出现反面的次数为X,则D(X)等于
√
1
2
3
4
√
1
2
3
4
解析 因为X~B(2,p),
所以P(X≥1)=1-P(X<1)=1-P(X=0)
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.设X~B(40,p),且E(X)=16,则p等于
A.0.1 B.0.2 C.0.3 D.0.4
√
解析 ∵E(X)=16,
∴40p=16,∴p=0.4.
√
所以n=36,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知随机变量X+Y=8,若X~B(10,0.6),则E(Y),D(Y)分别是
A.6和2.4 B.2和2.4
C.2和5.6 D.6和5.6
√
解析 因为X+Y=8,所以Y=8-X.
所以E(Y)=8-E(X)=8-10×0.6=2,
D(Y)=(-1)2D(X)=10×0.6×0.4=2.4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵P(ξ=0)+P(ξ≥1)=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 由二进制数A的特点知每一个数位上的数字只能填0,1,
且每个数位上的数字再填时互不影响,故以后的5位数中后4位的所有结果有4类:
①后4个数出现0,X=0,
②后4个数位只出现1个1,X=1,
③后4个数位出现2个1,X=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
④后4个数位上出现3个1,X=3,
⑤后4个数位都出现1,X=4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.一个病人服用某种新药后被治愈的概率为0.9,则服用这种新药的4个病人中至少3人被治愈的概率为________(用数字作答).
0.947 7
解析 由随机变量X~B(2,p),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求ξ的均值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 方法一 ξ的所有可能取值为0,1,2,3,4,
∴ξ的分布列为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求n和p的值,并写出X的概率分布;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由题意知,X~B(n,p),
由E(X)=np=3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X的概率分布为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率.
解 记“需要补种沙柳”为事件A,
则P(A)=P(X≤3),
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.袋中有3个白球和i个黑球,有放回的摸取3次,每次摸取一球,设摸得黑球的个数为ξi,其中i=1,2,则
A.E(ξ1)
C.E(ξ1)>E(ξ2),D(ξ1)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当i=1时,ξ1可能的取值为0,1,2,3,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当i=2时,ξ2可能的取值为0,1,2,3,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以E(ξ1)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.10 B.20 C.21 D.0
√
解析 由题意知
对比二项展开式得xk+yk=20,
所以符合题意的(xk,yk)有(0,20),(1,19),…,(20,0),共21个.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又k取整数,∴k=13.
拓广探究
15.掷骰子游戏:规定掷出1点,甲盒中放一球,掷出2点或3点,乙盒中放一球,掷出4点、5点或6点,丙盒中放一球,共掷6次,用x,y,z分别表示掷完6次后甲、乙、丙盒中球的个数.令X=x+y,则E(X)=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴E(z)=3,又x+y+z=6,
∴X=x+y=6-z,
∴E(X)=E(6-z)=6-E(z)=6-3=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设A1表示事件“日销售量不低于100个”,A2表示事件“日销售量低于50个”,B表示事件“在未来连续3天里有连续2天的日销售量不低于100个且另1天的日销售量低于50个”.
则P(A1)=(0.006+0.004+0.002)×50=0.6,
P(A2)=0.003×50=0.15,
P(B)=0.6×0.6×0.15×2=0.108.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的概率分布,均值E(X)及方差D(X).
解 X的可能取值为0,1,2,3,相应的概率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则X的概率分布为
X 0 1 2 3
P 0.064 0.288 0.432 0.216
因为X~B(3,0.6),所以均值E(X)=3×0.6=1.8,
方差D(X)=3×0.6×(1-0.6)=0.72.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
