北师大版数学八年级下册 第三章 图形的平移与旋转自我评估(一)(含答案)
文档属性
| 名称 | 北师大版数学八年级下册 第三章 图形的平移与旋转自我评估(一)(含答案) | 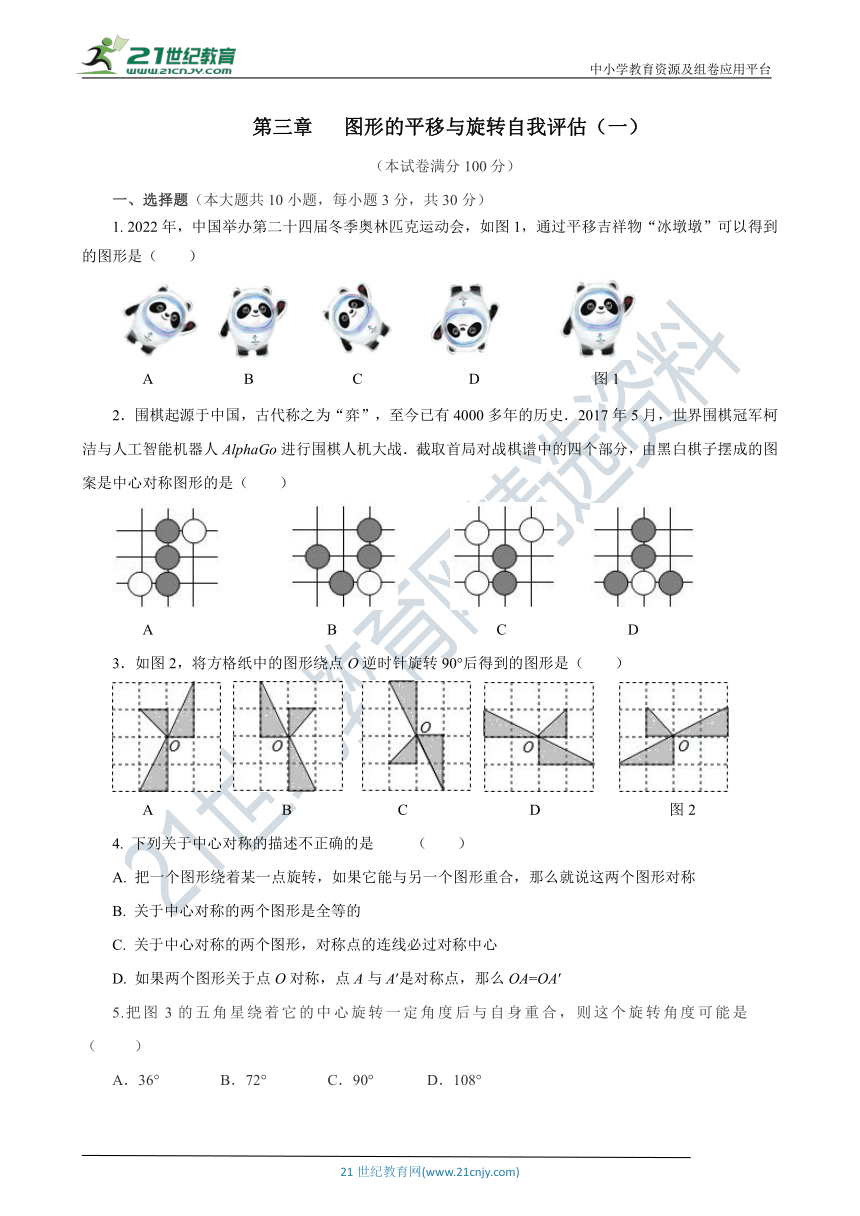 | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 09:35:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 图形的平移与旋转自我评估(一)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 2022年,中国举办第二十四届冬季奥林匹克运动会,如图1,通过平移吉祥物“冰墩墩”可以得到的图形是( )
A B C D 图1
2.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战.截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
A B C D
3.如图2,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )
A B C D 图2
4. 下列关于中心对称的描述不正确的是 ( )
A. 把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形对称
B. 关于中心对称的两个图形是全等的
C. 关于中心对称的两个图形,对称点的连线必过对称中心
D. 如果两个图形关于点O对称,点A与A′是对称点,那么OA=OA′
5.把图3的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A.36° B.72° C.90° D.108°
图3 图4 图5
6.已知平面直角坐标系中两点A(3,-1),B(-1,2),连接AB,平移线段AB得到线段A1B1.若点A的对应点是A1(1,2),则点B的对应点B1的坐标为( )
A.(2,-3) B.(-2,-1) C.(-3,5) D.(3,-1)
7.如图4,∠1=70°,直线a平移后得到直线b,则∠2的度数比∠3的度数大( )
A.70° B.80° C.110° D.180°
8.如图5,在△ABC中,∠C=90°,∠CAB=50°,点D在斜边AB上.如果△ABC绕点B旋转后与△EBD重合,连接AE,那么∠EAB的度数是( )
A.80° B.70° C.60° D.50°
9. 如图6,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论一定正确的是 ( )
A. ∠ABC=∠ADC B. CB=CD C. DE+DC=BC D. AB∥CD
图6 图7
如图7,在△ABC中,∠C=90°,AC=BC,AB=8,D为AB的中点.若直角∠MDN绕点D旋转,分别交AC,BC于点E,F,下列说法:①AE=CF;②EC+CF=;③DE=DF;④若△ECF的面积确定,则EF的长也是一个定值.
其中正确的有( )
①② B.③④ C.①③④ D.①②③④
二、填空题(本大题共6小题,每小题3分,共18分)
11.在平面直角坐标系中,点P(-5,6)关于原点对称的点的坐标是_____________.
12.如图8,将△ABC沿着射线BC的方向平移到△DEF的位置.若E是BC的中点,BF=18 cm,则平移的距离为 cm.
图8 图9 图10 图11
13.如图9,在平面直角坐标系xOy中,△OCD可以看成是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△OCD的过程: .
14.如图10,Rt△ABC的周长为22,在其内部有5个小直角三角形,且这5个小直角三角形都有一条边与BC平行,则这5个小直角三角形周长的和为 .
15.如图11,在△ABC中,边BC在直线MN上,且BC=9 cm,将△ABC沿直线MN平移得到△DEF,点B的对应点为E.若平移的距离为2 cm,则CE的长为 cm.
16.如图12,将长方形ABCD绕点A旋转至长方形AB′C′D′的位置,AB′交CD于点E.若∠ACD=30°,AB=3,,则△AEC的面积为 .
三、解答题(本大题共7小题,共52分)
17.(6分)如图13,已知长方形ABCD的长为5,宽为4,若将其沿着射线BC的方向平移到长方形EFGH处,则长方形CDEF的周长是长方形ABCD周长的,求长方形ABCD平移的距离.
图13
18.(6分)如图14,在△ABC中,∠BAC=120°,以BC为边向外作等边三角形BCD,连接AD,将△ABD绕点D按逆时针方向旋转60°得到△ECD,且点A,C,E在同一直线上.若AB=3,AC=2,求AD的长.
图14
19.(6分)如图15,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′,其中点A′,B′,C′分别为点A,B,C的对应点.
(1)画出△A′B′C′,并直接写出点C′的坐标: ;
(2)若AB边上一点P经过上述平移后的对应点为P′(x,y).直接写出用含x,y的代数式表示点P的坐标: ;
(3)一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过原来的图形作一次平移得到,则线段BC在一次平移过程中扫过的面积为: .
图15
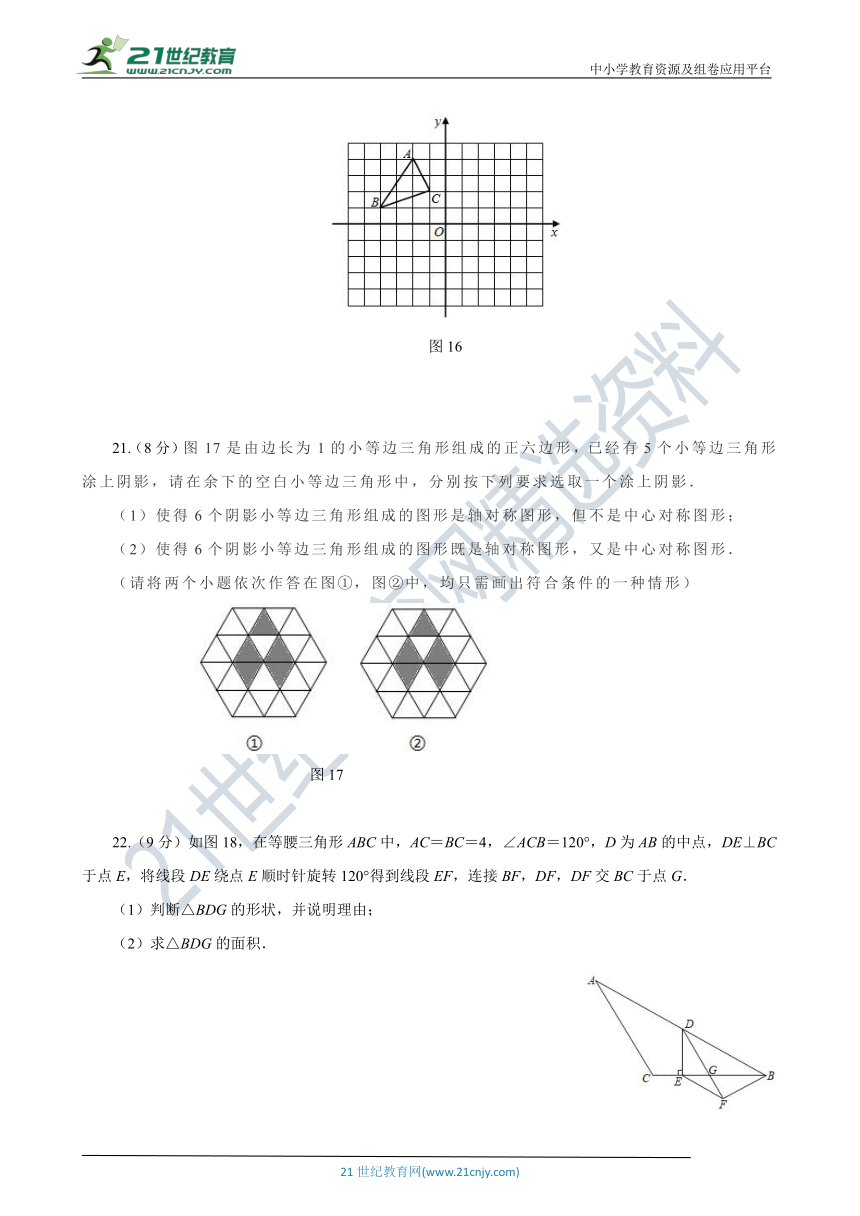
20.(7分)如图16,在平面直角坐标系中,已知A(-2,4),B(-4,1),C(-1,2).
(1)画出△ABC关于点O成中心对称的图形△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的图形△A2B2C2;
(3)求在(2)的条件下,线段AC扫过的面积.
图16
21.(8分)图17是由边长为1的小等边三角形组成的正六边形,已经有5个小等边三角形涂上阴影,请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影.
(1)使得6个阴影小等边三角形组成的图形是轴对称图形,但不是中心对称图形;
(2)使得6个阴影小等边三角形组成的图形既是轴对称图形,又是中心对称图形.
(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
图17
22.(9分)如图18,在等腰三角形ABC中,AC=BC=4,∠ACB=120°,D为AB的中点,DE⊥BC于点E,将线段DE绕点E顺时针旋转120°得到线段EF,连接BF,DF,DF交BC于点G.
(1)判断△BDG的形状,并说明理由;
(2)求△BDG的面积.
图18
23.(10分)阅读与理解:
图①是边长分别为a和b(a>b)的两个等边三角形ABC和CDE叠放在一起的图形.
操作与证明:
(1)操作:固定△ABC,将△CDE绕点C按顺时针方向旋转30°,连接AD,BE,如图②;在图②中,线段BE与AD之间具有怎样的数量关系?证明你的结论.
操作:若将图①中的△CDE,绕点C按顺时针方向任意旋转一个角度α(0°≤α≤360°),连接AD,BE,如图③,在图③中,线段BE与AD之间具有怎样的数量关系?证明你的结论.
猜想与发现:
(3)根据上面的操作过程,请你猜想:当α为多少度时,线段AD的长度最大,是多少?当α为多少度时,线段AD的长度最小,是多少?
① ② ③
图19
附加题(20分,不计入总分)
如图①,在平面直角坐标系中,点A,B在坐标轴上,其中A(0,a),B(b,0)满足.
(1)求A,B两点的坐标;
(2)将线段AB平移到CD,点A的对应点是C,点B的对应点是D,且C,D两点也在坐标轴上,过点O作直线OM⊥AB,垂足为M,交CD于点N,请在图①中画出图形,直接写出点C,D的坐标,并证明MN⊥CD;
(3)如图②,将AB平移到CD,点A的对应点为C(-2,m),连接AC,BC,BC交y轴于点E.若△ABC的面积等于13,求点E的坐标及m的值.
① ②
第三章 图形的平移与旋转自我评估(一)
答案速览
一、1. B 2.A 3.C 4.A 5.B 6. C 7. C 8.B 9.D 10. D
二、11.(5,-6) 12.6
13.将△AOB绕点O顺时针旋转90°,再向左平移2个单位长度得到△OCD(答案不唯一) 14.22
15. 7或11 16.
答案详解
10.D 解析:连接CD,利用“ASA”可证得△ADE≌△CDF,得出AE=CF,DE=DF,故①③正确;由①知,EC+CF=EC+AE=AC.又AC=BC,∠C=90°,AB=8,所以由勾股定理可求出AC=BC=,故②正确;因为S△ECF=CE CF,若S△ECF是一个定值,则CE CF是一个定值.由勾股定理,得EF2=CE2+CF2=(CE+CF)2-2CE CF.又CE+CF=,是一个确定的值,所以EF的长也是一个定值,故④正确.
16. 解析:因为四边形ABCD是长方形,所以AB∥CD,AB=CD=3,∠ADC=∠BAD=90°.
所以∠ACD=∠CAB=30°,∠DAC=60°.
由旋转,得∠DAE=∠CAB=30° .所以∠EAC=30°=∠ACD.
所以EA=EC.
设EA=EC=x,则有DE=CD-EC=3-x.
在Rt△ADE中,x2=(3-x)2+()2,解得x=2.所以EC=2.
则S△AEC=EC AD=.
三、17.解:设长方形ABCD平移的距离AE=x.
因为长方形ABCD的长为5,宽为4,所以长方形ABCD的周长为18.
因为长方形CDEF的周长是长方形ABCD周长的,所以4+4+5-x+5-x=18×,解得x=3.
所以长方形ABCD平移的距离为3.
18.解:因为△ABD绕着点D按逆时针方向旋转60°得到△ECD,所以∠ADE=60°,DE=DA,EC=AB.
又点A,C,E共线,所以△ADE是等边三角形.所以AD=AE.
因为AB=3,AC=2,所以AE=AC+EC=2+3=5.所以AD=5.
19.解:(1)图略.(4,2)
(2)(x-3,y-4)
(3)16
20.解:(1)(2)图略.
(3),, 线段AC扫过的面积为:.
21.解:(1)作图如图①所示(答案不唯一).(2)作图如图②所示.
① ②
22.解:(1)△BDG是等腰三角形.
理由:连接CD.
因为AC=BC=4,∠ACB=120°,D为AB的中点,所以CD⊥AB,∠DCE=∠ACB=60°,∠ABC=∠A=
(180°-∠ACB)=30°.
因为DE绕点E按顺时针旋转120°得到EF,所以DE=EF,∠DEF=120°.
所以∠EDG=∠EFD=(180°-∠DEF)=30°.
因为DE⊥BC,所以∠BDE=90°-∠ABC=30°.所以∠GDB=∠BDE-∠EDG=30°.
所以∠GDB=∠GBD.
所以△BDG是等腰三角形.
(2)因为CD⊥AB,∠ABC=30°,所以CD=BC=2.
因为∠CGD=∠GDB+∠GBD=30°+30°=60°,所以∠CDG=60°=∠CGD=∠DCG.
所以△CDG是等边三角形.
所以CG=CD=DG=2.
所以BG=DG=2.
因为DE⊥CG,所以.所以.
所以.
23.解:(1)BE=AD.
证明:因为△CDE绕点C按顺时针方向旋转30°,所以∠BCE=∠ACD=30°.
因为△ABC与△CDE都是等边三角形,所以CB=CA,CE=CD.所以△BCE≌△ACD.所以BE=AD.
(2)BE=AD.
证明:因为△CDE绕点C按顺时针方向旋转的角度为α,所以∠BCE=∠ACD=α.
因为△ABC与△CDE都是等边三角形,所以CB=CA,CE=CD.
所以△BCE≌△ACD.所以BE=AD.
(3)当α为180°时,线段AD的长度最大,等于a+b;当α为0°(或360°)时,线段AD的长度最小,等于a-b.
附加题
解:(1)因为|a-3|+=0,所以a=3,b=4.
所以A,B两点的坐标分别为(0,3),(4,0).
(2)C(-4,0),D(0,-3).
如图①,根据平移的性质,得AB∥CD,AB=CD.
因为OM⊥AB,所以OM⊥CD,即MN⊥CD.
① ②
(3)如图②,过点C作CF⊥y轴于点F.
因为S△ABC=13,即S△ACE+S△ABE=13,所以AE·CF+AE·OB=13.
所以(3+OE)×2+(3+OE)×4=13,解得OE=.
所以点E的坐标为(0,-).
设直线BE的表达式为y=kx+b.
根据题意,得解得
所以直线BE的表达式为y=x-.
当x=-2时,y=-2.所以m的值为-2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第三章 图形的平移与旋转自我评估(一)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 2022年,中国举办第二十四届冬季奥林匹克运动会,如图1,通过平移吉祥物“冰墩墩”可以得到的图形是( )
A B C D 图1
2.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战.截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
A B C D
3.如图2,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )
A B C D 图2
4. 下列关于中心对称的描述不正确的是 ( )
A. 把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形对称
B. 关于中心对称的两个图形是全等的
C. 关于中心对称的两个图形,对称点的连线必过对称中心
D. 如果两个图形关于点O对称,点A与A′是对称点,那么OA=OA′
5.把图3的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A.36° B.72° C.90° D.108°
图3 图4 图5
6.已知平面直角坐标系中两点A(3,-1),B(-1,2),连接AB,平移线段AB得到线段A1B1.若点A的对应点是A1(1,2),则点B的对应点B1的坐标为( )
A.(2,-3) B.(-2,-1) C.(-3,5) D.(3,-1)
7.如图4,∠1=70°,直线a平移后得到直线b,则∠2的度数比∠3的度数大( )
A.70° B.80° C.110° D.180°
8.如图5,在△ABC中,∠C=90°,∠CAB=50°,点D在斜边AB上.如果△ABC绕点B旋转后与△EBD重合,连接AE,那么∠EAB的度数是( )
A.80° B.70° C.60° D.50°
9. 如图6,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论一定正确的是 ( )
A. ∠ABC=∠ADC B. CB=CD C. DE+DC=BC D. AB∥CD
图6 图7
如图7,在△ABC中,∠C=90°,AC=BC,AB=8,D为AB的中点.若直角∠MDN绕点D旋转,分别交AC,BC于点E,F,下列说法:①AE=CF;②EC+CF=;③DE=DF;④若△ECF的面积确定,则EF的长也是一个定值.
其中正确的有( )
①② B.③④ C.①③④ D.①②③④
二、填空题(本大题共6小题,每小题3分,共18分)
11.在平面直角坐标系中,点P(-5,6)关于原点对称的点的坐标是_____________.
12.如图8,将△ABC沿着射线BC的方向平移到△DEF的位置.若E是BC的中点,BF=18 cm,则平移的距离为 cm.
图8 图9 图10 图11
13.如图9,在平面直角坐标系xOy中,△OCD可以看成是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△OCD的过程: .
14.如图10,Rt△ABC的周长为22,在其内部有5个小直角三角形,且这5个小直角三角形都有一条边与BC平行,则这5个小直角三角形周长的和为 .
15.如图11,在△ABC中,边BC在直线MN上,且BC=9 cm,将△ABC沿直线MN平移得到△DEF,点B的对应点为E.若平移的距离为2 cm,则CE的长为 cm.
16.如图12,将长方形ABCD绕点A旋转至长方形AB′C′D′的位置,AB′交CD于点E.若∠ACD=30°,AB=3,,则△AEC的面积为 .
三、解答题(本大题共7小题,共52分)
17.(6分)如图13,已知长方形ABCD的长为5,宽为4,若将其沿着射线BC的方向平移到长方形EFGH处,则长方形CDEF的周长是长方形ABCD周长的,求长方形ABCD平移的距离.
图13
18.(6分)如图14,在△ABC中,∠BAC=120°,以BC为边向外作等边三角形BCD,连接AD,将△ABD绕点D按逆时针方向旋转60°得到△ECD,且点A,C,E在同一直线上.若AB=3,AC=2,求AD的长.
图14
19.(6分)如图15,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′,其中点A′,B′,C′分别为点A,B,C的对应点.
(1)画出△A′B′C′,并直接写出点C′的坐标: ;
(2)若AB边上一点P经过上述平移后的对应点为P′(x,y).直接写出用含x,y的代数式表示点P的坐标: ;
(3)一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过原来的图形作一次平移得到,则线段BC在一次平移过程中扫过的面积为: .
图15
20.(7分)如图16,在平面直角坐标系中,已知A(-2,4),B(-4,1),C(-1,2).
(1)画出△ABC关于点O成中心对称的图形△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的图形△A2B2C2;
(3)求在(2)的条件下,线段AC扫过的面积.
图16
21.(8分)图17是由边长为1的小等边三角形组成的正六边形,已经有5个小等边三角形涂上阴影,请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影.
(1)使得6个阴影小等边三角形组成的图形是轴对称图形,但不是中心对称图形;
(2)使得6个阴影小等边三角形组成的图形既是轴对称图形,又是中心对称图形.
(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
图17
22.(9分)如图18,在等腰三角形ABC中,AC=BC=4,∠ACB=120°,D为AB的中点,DE⊥BC于点E,将线段DE绕点E顺时针旋转120°得到线段EF,连接BF,DF,DF交BC于点G.
(1)判断△BDG的形状,并说明理由;
(2)求△BDG的面积.
图18
23.(10分)阅读与理解:
图①是边长分别为a和b(a>b)的两个等边三角形ABC和CDE叠放在一起的图形.
操作与证明:
(1)操作:固定△ABC,将△CDE绕点C按顺时针方向旋转30°,连接AD,BE,如图②;在图②中,线段BE与AD之间具有怎样的数量关系?证明你的结论.
操作:若将图①中的△CDE,绕点C按顺时针方向任意旋转一个角度α(0°≤α≤360°),连接AD,BE,如图③,在图③中,线段BE与AD之间具有怎样的数量关系?证明你的结论.
猜想与发现:
(3)根据上面的操作过程,请你猜想:当α为多少度时,线段AD的长度最大,是多少?当α为多少度时,线段AD的长度最小,是多少?
① ② ③
图19
附加题(20分,不计入总分)
如图①,在平面直角坐标系中,点A,B在坐标轴上,其中A(0,a),B(b,0)满足.
(1)求A,B两点的坐标;
(2)将线段AB平移到CD,点A的对应点是C,点B的对应点是D,且C,D两点也在坐标轴上,过点O作直线OM⊥AB,垂足为M,交CD于点N,请在图①中画出图形,直接写出点C,D的坐标,并证明MN⊥CD;
(3)如图②,将AB平移到CD,点A的对应点为C(-2,m),连接AC,BC,BC交y轴于点E.若△ABC的面积等于13,求点E的坐标及m的值.
① ②
第三章 图形的平移与旋转自我评估(一)
答案速览
一、1. B 2.A 3.C 4.A 5.B 6. C 7. C 8.B 9.D 10. D
二、11.(5,-6) 12.6
13.将△AOB绕点O顺时针旋转90°,再向左平移2个单位长度得到△OCD(答案不唯一) 14.22
15. 7或11 16.
答案详解
10.D 解析:连接CD,利用“ASA”可证得△ADE≌△CDF,得出AE=CF,DE=DF,故①③正确;由①知,EC+CF=EC+AE=AC.又AC=BC,∠C=90°,AB=8,所以由勾股定理可求出AC=BC=,故②正确;因为S△ECF=CE CF,若S△ECF是一个定值,则CE CF是一个定值.由勾股定理,得EF2=CE2+CF2=(CE+CF)2-2CE CF.又CE+CF=,是一个确定的值,所以EF的长也是一个定值,故④正确.
16. 解析:因为四边形ABCD是长方形,所以AB∥CD,AB=CD=3,∠ADC=∠BAD=90°.
所以∠ACD=∠CAB=30°,∠DAC=60°.
由旋转,得∠DAE=∠CAB=30° .所以∠EAC=30°=∠ACD.
所以EA=EC.
设EA=EC=x,则有DE=CD-EC=3-x.
在Rt△ADE中,x2=(3-x)2+()2,解得x=2.所以EC=2.
则S△AEC=EC AD=.
三、17.解:设长方形ABCD平移的距离AE=x.
因为长方形ABCD的长为5,宽为4,所以长方形ABCD的周长为18.
因为长方形CDEF的周长是长方形ABCD周长的,所以4+4+5-x+5-x=18×,解得x=3.
所以长方形ABCD平移的距离为3.
18.解:因为△ABD绕着点D按逆时针方向旋转60°得到△ECD,所以∠ADE=60°,DE=DA,EC=AB.
又点A,C,E共线,所以△ADE是等边三角形.所以AD=AE.
因为AB=3,AC=2,所以AE=AC+EC=2+3=5.所以AD=5.
19.解:(1)图略.(4,2)
(2)(x-3,y-4)
(3)16
20.解:(1)(2)图略.
(3),, 线段AC扫过的面积为:.
21.解:(1)作图如图①所示(答案不唯一).(2)作图如图②所示.
① ②
22.解:(1)△BDG是等腰三角形.
理由:连接CD.
因为AC=BC=4,∠ACB=120°,D为AB的中点,所以CD⊥AB,∠DCE=∠ACB=60°,∠ABC=∠A=
(180°-∠ACB)=30°.
因为DE绕点E按顺时针旋转120°得到EF,所以DE=EF,∠DEF=120°.
所以∠EDG=∠EFD=(180°-∠DEF)=30°.
因为DE⊥BC,所以∠BDE=90°-∠ABC=30°.所以∠GDB=∠BDE-∠EDG=30°.
所以∠GDB=∠GBD.
所以△BDG是等腰三角形.
(2)因为CD⊥AB,∠ABC=30°,所以CD=BC=2.
因为∠CGD=∠GDB+∠GBD=30°+30°=60°,所以∠CDG=60°=∠CGD=∠DCG.
所以△CDG是等边三角形.
所以CG=CD=DG=2.
所以BG=DG=2.
因为DE⊥CG,所以.所以.
所以.
23.解:(1)BE=AD.
证明:因为△CDE绕点C按顺时针方向旋转30°,所以∠BCE=∠ACD=30°.
因为△ABC与△CDE都是等边三角形,所以CB=CA,CE=CD.所以△BCE≌△ACD.所以BE=AD.
(2)BE=AD.
证明:因为△CDE绕点C按顺时针方向旋转的角度为α,所以∠BCE=∠ACD=α.
因为△ABC与△CDE都是等边三角形,所以CB=CA,CE=CD.
所以△BCE≌△ACD.所以BE=AD.
(3)当α为180°时,线段AD的长度最大,等于a+b;当α为0°(或360°)时,线段AD的长度最小,等于a-b.
附加题
解:(1)因为|a-3|+=0,所以a=3,b=4.
所以A,B两点的坐标分别为(0,3),(4,0).
(2)C(-4,0),D(0,-3).
如图①,根据平移的性质,得AB∥CD,AB=CD.
因为OM⊥AB,所以OM⊥CD,即MN⊥CD.
① ②
(3)如图②,过点C作CF⊥y轴于点F.
因为S△ABC=13,即S△ACE+S△ABE=13,所以AE·CF+AE·OB=13.
所以(3+OE)×2+(3+OE)×4=13,解得OE=.
所以点E的坐标为(0,-).
设直线BE的表达式为y=kx+b.
根据题意,得解得
所以直线BE的表达式为y=x-.
当x=-2时,y=-2.所以m的值为-2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
