北师大版数学八年级下册第三章 图形的平移与旋转自我评估(二)(含答案)
文档属性
| 名称 | 北师大版数学八年级下册第三章 图形的平移与旋转自我评估(二)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 12:41:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 图形的平移与旋转自我评估(二)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列关于防范“新冠肺炎”的标志中,既是轴对称图形,又是中心对称图形的是( )
戴口罩讲卫生 勤洗手勤通风
A B
有症状早就医 少出门少聚集
C D
2.中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”.通过平移,可将图1中的吉祥物“海宝”平移到图( )
A. B. C. D.
3.下列运动属于旋转的是( )
A.火箭升空的运动 B.足球在草地上滚动
C.风车运动的过程 D.传输带上物品的运动
4.点M(1,2)关于原点对称的点的坐标是( )
A.(-1,2) B.(1,2) C.(-1,-2) D.(-2,1)
5.在平面直角坐标系中,将点(-2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为( )
A.(2,5) B.(﹣6,5) C.(2,1) D.(﹣6,1)
6.如图2中的三角形甲可以通过哪种运动和三角形乙重合( )
A.平移 B.旋转
C.平移后再旋转 D.翻折
图2 图3 图4 图5
7.图3是一个标准的五角星,若将它绕旋转中心旋转一定的角度后能与自身重合,则至少应将它旋转的度数是( )
A.144° B.90° C.72° D.60°
8.如图4,把△ABC绕点C逆时针旋转90°得到△DCE,若BE=17,AD=7,则BC的长为( )
A.3 B.4 C.5 D.6
9. 如图5,在△ABC中,∠BAC=90°,AB=3 cm,AC=4 cm,把△ABC沿直线BC向右平移2.5 cm后得到△DEF,连接AE,AD,有以下结论:①BF=7.5 cm;②AD∥BE;③CF=2.5 cm;④DE⊥AC.
其中正确的有( )
1个 B. 2个 C. 3个 D. 4个
如图6,平面内某正方形内有一个长为10,宽为5的长方形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10 B.11 C.12 D.13
图6
二、填空题(本大题共6小题,每小题3分,共18分)
11.如图7,已知△ABC与△DEC关于点C成中心对称.若AB=2,则DE= .
图7 图8 图9
12.如图8,将△OAB绕点O逆时针旋转70°到△OCD的位置.若∠AOB=40°,则∠AOD= °.
13.如图9,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为 .
14.在图10所示的草坪上,铺设一条水平宽度为2的小路,则草坪的面积为 .
图10 图11 图12
如图11,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是_____________ cm.
16.如图12,在△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A'OB'处,此时线段A'B'与BO的交点E为BO的中点,则线段B'E的长为 .
三、解答题(本大题7小题,共52分)
17.(5分)如图13,在△ABC中,∠C=90°,CB=6,CA=8,将△ABC绕点B顺时针旋转得到△DBE,使点C的对应点E恰好落在AB上,求线段AE的长.
图13
18.(5分)已知△ABC与△A'B'C'在平面直角坐标系中的位置如图14所示.
(1)分别写出下列各点的坐标:A ,B ,C .
(2)△ABC是由△A'B'C'经过怎样的平移得到的?
(3)求△ABC的面积.
图14
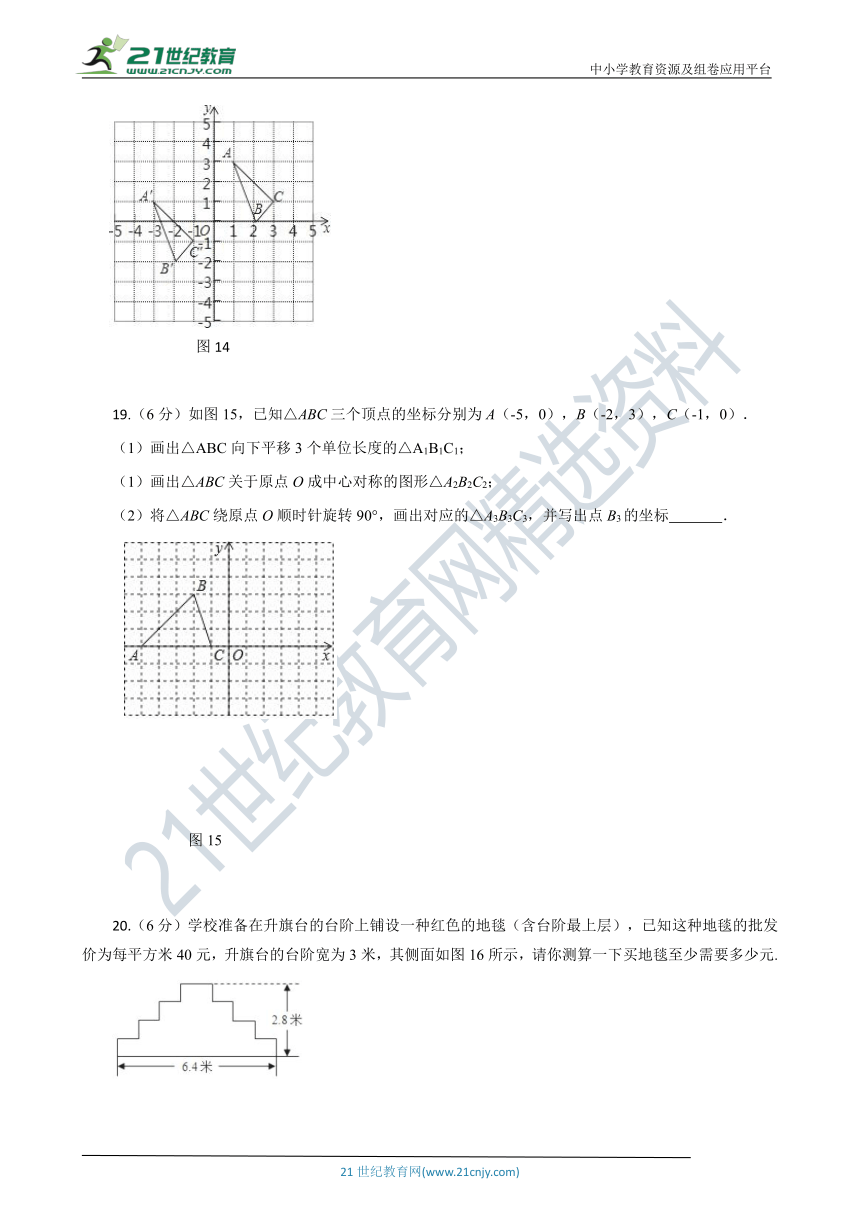
19.(6分)如图15,已知△ABC三个顶点的坐标分别为A(-5,0),B(-2,3),C(-1,0).
(1)画出△ABC向下平移3个单位长度的△A1B1C1;
(1)画出△ABC关于原点O成中心对称的图形△A2B2C2;
(2)将△ABC绕原点O顺时针旋转90°,画出对应的△A3B3C3,并写出点B3的坐标 .
图15
20.(6分)学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图16所示,请你测算一下买地毯至少需要多少元.
图16
21.(8分)如图17,方格纸中有三个点A,B,C,要求作一个四边形,使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
图17
22.(10分)如图18,将△ABC沿射线BA方向平移到△A′B′C′的位置,连接AC′.
(1)AA′与CC′的位置关系为 ;
(2)求证:∠A′+∠CAC′+∠AC′C=180°;
(3)设∠AC′B′=x,∠ACB=y,试探索∠CAC′与x,y之间的数量关系,并证明你的结论.
图18
23.(12分)如图19,在正方形ABCD中,E,F是对角线BD上的两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1求证:EA是∠QED的平分线;
(2)求证:EF2=BE2+DF2.
图19
附加题(20分,不计入总分)
如图①,已知边长为6的等边三角形ABC中,点D,E分别在AC,BC边上,DE∥AB,EC=.将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,如图②,连接AD′,BE′,P为边D′E′的中点.
(1)在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
(2)连接AP,当AP最大时,求AD′的长度.(结果保留根号)
第三章 图形的平移与旋转自我评估(二)
一、1.C 2.B 3.C 4.C 5.C 6.D 7.C 8.C 9.D
10.C 提示:根据长方形的长为10,宽为5,可得长方形的对角线长为,由长方形可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,可得该正方形的边长不小于5,由11<5<12,可知该正方形边长的最小整数n为12.
二、11.2 12.30 13.(3,-2) 14.104 15.2
提示:由勾股定理求出AB,由旋转的性质可得AO=A′O,A′B′=AB,由OE=4,得到OE=A′O,过点O作OF⊥A′B′于点F,由三角形的面积求出OF,由勾股定理列式求出EF,再由等腰三角形“三线合一”的性质可得A′E=2EF,然后由B′E=A′B′-A′E可求得结果.
三、17. 解:在△ABC中,∠C=90°,CB=6,CA=8,由勾股定理,得AB==10.
由旋转的性质,得BE=BC=6,所以AE=AB﹣BE=10﹣6=4.
18.解:(1)A(1,3),B(2,0),C(3,1);
(2)△ABC由△A'B'C'先向右平移4个单位长度,再向上平移2个单位长度(或先向上平移2个单位长度,再向右平移4个单位长度)得到的;
(3)S△ABC=2×3-×1×3-×1×1-×2×2=2.
19.解:(1)如图1,△A1B1C1为所求作;
(1)如图1,△A2B2C2为所求作;
(2)如图1,△A3B3C3为所求作,点B3的坐标为(3,2).
图1
20.解:利用平移把台阶的横竖分别平移,构成一个长、宽分别为6.4米,2.8米的长方形.
所以地毯的长度为6.4+2.8+2.8=12(米),地毯的面积为12×3=36(平方米).
所以买地毯至少需要36×40=1440(元).
21.解:(1)如图2-甲;(2)如图2-乙;(3)如图2-丙.
图2
22.解:(1)AA′∥CC′
(2)根据平移性质,得∠A′=∠BAC,AA'∥CC',即BA'∥CC'.
所以∠BAC'+∠AC′C=180°,∠BAC+∠CAC′+∠AC′C=180°.
所以∠A'+∠CAC'+∠AC'C=180°.
(3)∠CAC'=x+y.
证明:过点A作AD∥BC,交CC'于点D.
根据平移性质,得B'C'∥BC.
所以B'C'∥AD∥BC.
所以∠AC'B'=∠C'AD,∠ACB=∠DAC.
所以∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y.
23.证明:(1)因为将△ADF绕点A顺时针旋转90°后得到△ABQ,所以BQ=DF,AQ=AF,∠BAQ=∠DAF.
因为∠EAF=45°,所以∠DAF+∠BAE=45°.所以∠QAE=45°.所以∠QAE=∠FAE.
在△AQE和△AFE中,AQ=AF,∠QAE=∠FAE,AE=AE,所以△AQE≌△AFE(SAS).
所以∠AEQ=∠AEF.所以EA是∠QED的平分线.
(2)由(1),得△AQE≌△AFE,所以EQ=EF.
因为四边形ABCD是正方形,所以AD=AB,∠BAD=90°.所以∠ADF=∠ABD=45°.
所以∠ABQ=45°.所以∠QBE=90°.
在Rt△QBE中,BE2+ QB2=EQ2. 因为QB=DF,所以EF2=BE2+DF2.
附加题
解:(1)AD′=BE′.理由:当α≠180°时,由旋转的性质,得∠ACD′=∠BCE′.
因为△ABC是等边三角形,所以AC=BC,∠ABC=∠ACB=60°.
因为DE∥AB,所以∠DEC=∠ABC =60°.所以△DEC是等边三角形.
由旋转的性质,知△D′E′C是等边三角形.所以CD′=CE′.又∠ACD′=∠BCE′,所以△ACD′≌△BCE′.所以AD′=BE′;
当α=180°时,AD′=AC+CD′,BE′=BC+CE′,即AD′=BE′.
综上可知,AD′=BE′.
(2)连接CP.
在△ACP中,由三角形的三边关系,得AP<AC+CP,所以当A,C,P三点共线时,AP最大.
如图所示,在△D′CE′中,因为P为D′E′的中点,所以AP⊥D′E′,PD′=D′E′.
由(1),知△D′E′C是等边三角形,且D′E′=CD′=E′C=EC=,所以PD′=.
在Rt△CPD′中,由勾股定理,得CP==3.所以AP=6+3=9.
在Rt△APD′中,由勾股定理,得AD′==.
_21?????????è?????(www.21cnjy.com)_
第三章 图形的平移与旋转自我评估(二)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列关于防范“新冠肺炎”的标志中,既是轴对称图形,又是中心对称图形的是( )
戴口罩讲卫生 勤洗手勤通风
A B
有症状早就医 少出门少聚集
C D
2.中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”.通过平移,可将图1中的吉祥物“海宝”平移到图( )
A. B. C. D.
3.下列运动属于旋转的是( )
A.火箭升空的运动 B.足球在草地上滚动
C.风车运动的过程 D.传输带上物品的运动
4.点M(1,2)关于原点对称的点的坐标是( )
A.(-1,2) B.(1,2) C.(-1,-2) D.(-2,1)
5.在平面直角坐标系中,将点(-2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为( )
A.(2,5) B.(﹣6,5) C.(2,1) D.(﹣6,1)
6.如图2中的三角形甲可以通过哪种运动和三角形乙重合( )
A.平移 B.旋转
C.平移后再旋转 D.翻折
图2 图3 图4 图5
7.图3是一个标准的五角星,若将它绕旋转中心旋转一定的角度后能与自身重合,则至少应将它旋转的度数是( )
A.144° B.90° C.72° D.60°
8.如图4,把△ABC绕点C逆时针旋转90°得到△DCE,若BE=17,AD=7,则BC的长为( )
A.3 B.4 C.5 D.6
9. 如图5,在△ABC中,∠BAC=90°,AB=3 cm,AC=4 cm,把△ABC沿直线BC向右平移2.5 cm后得到△DEF,连接AE,AD,有以下结论:①BF=7.5 cm;②AD∥BE;③CF=2.5 cm;④DE⊥AC.
其中正确的有( )
1个 B. 2个 C. 3个 D. 4个
如图6,平面内某正方形内有一个长为10,宽为5的长方形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10 B.11 C.12 D.13
图6
二、填空题(本大题共6小题,每小题3分,共18分)
11.如图7,已知△ABC与△DEC关于点C成中心对称.若AB=2,则DE= .
图7 图8 图9
12.如图8,将△OAB绕点O逆时针旋转70°到△OCD的位置.若∠AOB=40°,则∠AOD= °.
13.如图9,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为 .
14.在图10所示的草坪上,铺设一条水平宽度为2的小路,则草坪的面积为 .
图10 图11 图12
如图11,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是_____________ cm.
16.如图12,在△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A'OB'处,此时线段A'B'与BO的交点E为BO的中点,则线段B'E的长为 .
三、解答题(本大题7小题,共52分)
17.(5分)如图13,在△ABC中,∠C=90°,CB=6,CA=8,将△ABC绕点B顺时针旋转得到△DBE,使点C的对应点E恰好落在AB上,求线段AE的长.
图13
18.(5分)已知△ABC与△A'B'C'在平面直角坐标系中的位置如图14所示.
(1)分别写出下列各点的坐标:A ,B ,C .
(2)△ABC是由△A'B'C'经过怎样的平移得到的?
(3)求△ABC的面积.
图14
19.(6分)如图15,已知△ABC三个顶点的坐标分别为A(-5,0),B(-2,3),C(-1,0).
(1)画出△ABC向下平移3个单位长度的△A1B1C1;
(1)画出△ABC关于原点O成中心对称的图形△A2B2C2;
(2)将△ABC绕原点O顺时针旋转90°,画出对应的△A3B3C3,并写出点B3的坐标 .
图15
20.(6分)学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图16所示,请你测算一下买地毯至少需要多少元.
图16
21.(8分)如图17,方格纸中有三个点A,B,C,要求作一个四边形,使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
图17
22.(10分)如图18,将△ABC沿射线BA方向平移到△A′B′C′的位置,连接AC′.
(1)AA′与CC′的位置关系为 ;
(2)求证:∠A′+∠CAC′+∠AC′C=180°;
(3)设∠AC′B′=x,∠ACB=y,试探索∠CAC′与x,y之间的数量关系,并证明你的结论.
图18
23.(12分)如图19,在正方形ABCD中,E,F是对角线BD上的两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1求证:EA是∠QED的平分线;
(2)求证:EF2=BE2+DF2.
图19
附加题(20分,不计入总分)
如图①,已知边长为6的等边三角形ABC中,点D,E分别在AC,BC边上,DE∥AB,EC=.将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,如图②,连接AD′,BE′,P为边D′E′的中点.
(1)在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
(2)连接AP,当AP最大时,求AD′的长度.(结果保留根号)
第三章 图形的平移与旋转自我评估(二)
一、1.C 2.B 3.C 4.C 5.C 6.D 7.C 8.C 9.D
10.C 提示:根据长方形的长为10,宽为5,可得长方形的对角线长为,由长方形可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,可得该正方形的边长不小于5,由11<5<12,可知该正方形边长的最小整数n为12.
二、11.2 12.30 13.(3,-2) 14.104 15.2
提示:由勾股定理求出AB,由旋转的性质可得AO=A′O,A′B′=AB,由OE=4,得到OE=A′O,过点O作OF⊥A′B′于点F,由三角形的面积求出OF,由勾股定理列式求出EF,再由等腰三角形“三线合一”的性质可得A′E=2EF,然后由B′E=A′B′-A′E可求得结果.
三、17. 解:在△ABC中,∠C=90°,CB=6,CA=8,由勾股定理,得AB==10.
由旋转的性质,得BE=BC=6,所以AE=AB﹣BE=10﹣6=4.
18.解:(1)A(1,3),B(2,0),C(3,1);
(2)△ABC由△A'B'C'先向右平移4个单位长度,再向上平移2个单位长度(或先向上平移2个单位长度,再向右平移4个单位长度)得到的;
(3)S△ABC=2×3-×1×3-×1×1-×2×2=2.
19.解:(1)如图1,△A1B1C1为所求作;
(1)如图1,△A2B2C2为所求作;
(2)如图1,△A3B3C3为所求作,点B3的坐标为(3,2).
图1
20.解:利用平移把台阶的横竖分别平移,构成一个长、宽分别为6.4米,2.8米的长方形.
所以地毯的长度为6.4+2.8+2.8=12(米),地毯的面积为12×3=36(平方米).
所以买地毯至少需要36×40=1440(元).
21.解:(1)如图2-甲;(2)如图2-乙;(3)如图2-丙.
图2
22.解:(1)AA′∥CC′
(2)根据平移性质,得∠A′=∠BAC,AA'∥CC',即BA'∥CC'.
所以∠BAC'+∠AC′C=180°,∠BAC+∠CAC′+∠AC′C=180°.
所以∠A'+∠CAC'+∠AC'C=180°.
(3)∠CAC'=x+y.
证明:过点A作AD∥BC,交CC'于点D.
根据平移性质,得B'C'∥BC.
所以B'C'∥AD∥BC.
所以∠AC'B'=∠C'AD,∠ACB=∠DAC.
所以∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y.
23.证明:(1)因为将△ADF绕点A顺时针旋转90°后得到△ABQ,所以BQ=DF,AQ=AF,∠BAQ=∠DAF.
因为∠EAF=45°,所以∠DAF+∠BAE=45°.所以∠QAE=45°.所以∠QAE=∠FAE.
在△AQE和△AFE中,AQ=AF,∠QAE=∠FAE,AE=AE,所以△AQE≌△AFE(SAS).
所以∠AEQ=∠AEF.所以EA是∠QED的平分线.
(2)由(1),得△AQE≌△AFE,所以EQ=EF.
因为四边形ABCD是正方形,所以AD=AB,∠BAD=90°.所以∠ADF=∠ABD=45°.
所以∠ABQ=45°.所以∠QBE=90°.
在Rt△QBE中,BE2+ QB2=EQ2. 因为QB=DF,所以EF2=BE2+DF2.
附加题
解:(1)AD′=BE′.理由:当α≠180°时,由旋转的性质,得∠ACD′=∠BCE′.
因为△ABC是等边三角形,所以AC=BC,∠ABC=∠ACB=60°.
因为DE∥AB,所以∠DEC=∠ABC =60°.所以△DEC是等边三角形.
由旋转的性质,知△D′E′C是等边三角形.所以CD′=CE′.又∠ACD′=∠BCE′,所以△ACD′≌△BCE′.所以AD′=BE′;
当α=180°时,AD′=AC+CD′,BE′=BC+CE′,即AD′=BE′.
综上可知,AD′=BE′.
(2)连接CP.
在△ACP中,由三角形的三边关系,得AP<AC+CP,所以当A,C,P三点共线时,AP最大.
如图所示,在△D′CE′中,因为P为D′E′的中点,所以AP⊥D′E′,PD′=D′E′.
由(1),知△D′E′C是等边三角形,且D′E′=CD′=E′C=EC=,所以PD′=.
在Rt△CPD′中,由勾股定理,得CP==3.所以AP=6+3=9.
在Rt△APD′中,由勾股定理,得AD′==.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
