北师大版数学七年级下册第二章 相交线与平行线综合测评(一)(含答案)
文档属性
| 名称 | 北师大版数学七年级下册第二章 相交线与平行线综合测评(一)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 10:27:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章 相交线与平行线综合测评(一)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 如图1,直线a,b被直线c所截,则∠1与∠2的位置关系是( )
A. 同位角 B. 内错角 C. 同旁内角 D. 互为补角
图1
2. 已知∠A与∠B互余,若∠A=60°,则∠B的度数为( )
A.30° B.60° C.120° D.150°
3. 在平面内,到直线l的距离等于2 cm的点有( )
A. 0个 B. 2个 C. 3个 D. 无数个
4. 下列四个图中,∠1=∠2一定成立的是( )
A B C D
5. 如图2,直线a,b被直线c所截,下列条件一定能判定直线a∥b的是( )
A.∠1=∠3 B.∠1=∠4 C.∠2=∠3 D.∠2+∠4=180°
图2 图3 图4 图5
6. 如图3,直线a,b相交于点O,如果∠1+∠2=110°,那么∠3的度数是( )
A. 125° B. 110° C. 70° D. 55°
7. 一把直尺与一把含有30°角的直角三角尺按图4所示的方式放置,若∠1=45°,则∠2的度数为( )
A. 45° B. 60° C. 65° D. 75°
8. 如图5,已知AB∥CD,若∠A=60°,∠ECD=120°,则∠ECA的度数是( )
A. 90° B. 120° C. 135° D. 150°
9.有下列说法:
①在同一平面内,两条直线的位置关系有平行、相交、垂直三种;
②平面内,过一点有且只有一条直线与已知直线垂直;
③过直线外一点有且只有一条直线与已知直线平行;
④同角或等角的补角相等.
其中正确的说法有( )
A.4?个 B.3?个 C.2?个 D.1?个
10. 如图6,有下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE,且∠ADC=∠B;④AB∥CE,且∠BCD=
∠BAD. 其中能推出BC∥AD的条件为( )
A. ①② B. ①②④ C. ①②③ D. ②③④
图6
二、填空题(本大题共6小题,每小题3分,共18分)
11. 若α=70°,则α的补角的度数是__________.
12. 如图7,已知AB⊥l1,AC⊥l2,若AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
图7 图8 图9 图10 图11
如图8,射线CA与直线BE交于点O,已知∠C=65°,请你添加一个条件__________________ ,使得BE∥CD.
14. 如图9,已知AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如
图所示的方式摆放,若∠EMB=75°,则∠PNM= .
15. 如图10,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BON=50°,则∠BOD的度数为_________.
16. 如图11,按虚线剪去长方形纸片(长方形的对边分别平行)的相邻两个角,并使∠1=120°,AB⊥BC,
那么∠2的度数为 .
三、解答题(本大题共6小题,共52分)
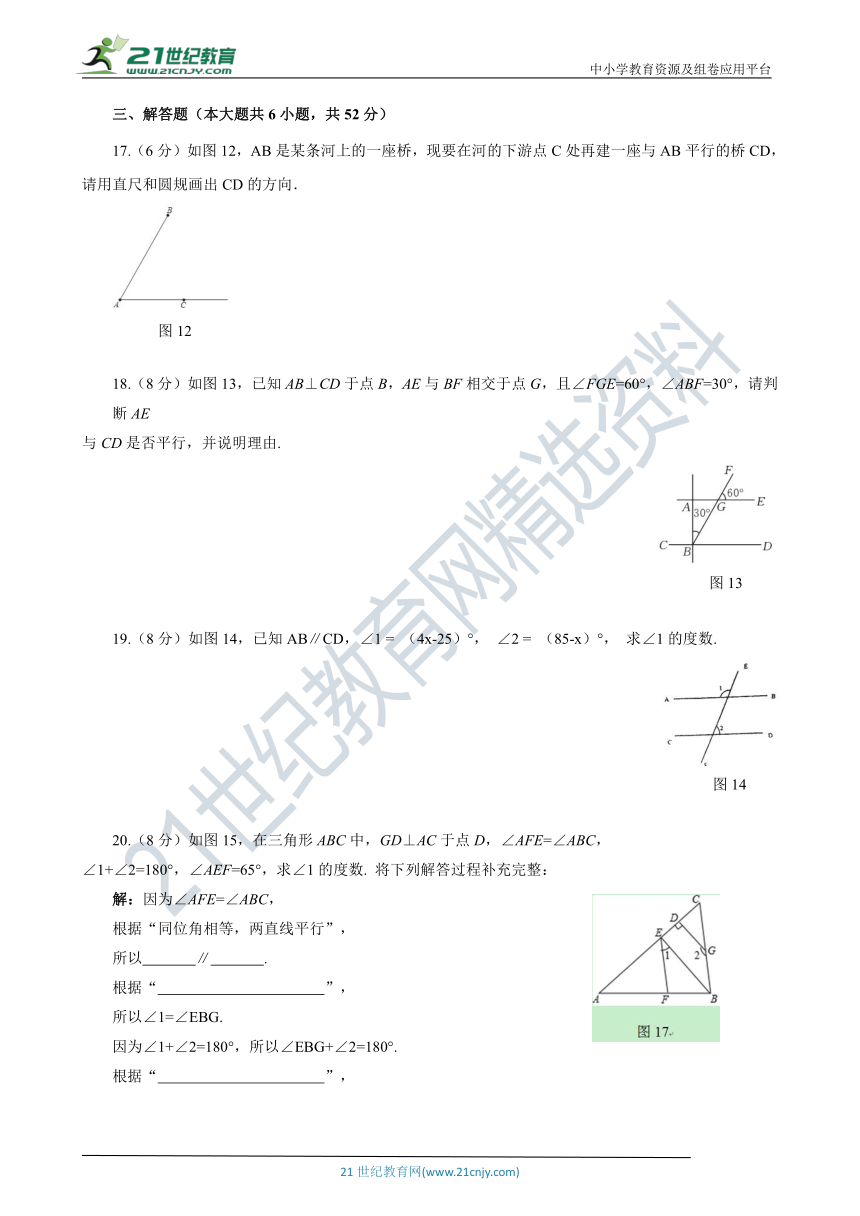
17.(6分)如图12,AB是某条河上的一座桥,现要在河的下游点C处再建一座与AB平行的桥CD,请用直尺和圆规画出CD的方向.
图12
18.(8分)如图13,已知AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,∠ABF=30°,请判断AE
与CD是否平行,并说明理由.
图13
19.(8分)如图14,已知AB∥CD,∠1 = (4x-25)°, ∠2 = (85-x)°, 求∠1的度数.
图14
20.(8分)如图15,在三角形ABC中,GD⊥AC于点D,∠AFE=∠ABC,
∠1+∠2=180°,∠AEF=65°,求∠1的度数. 将下列解答过程补充完整:
解:因为∠AFE=∠ABC,
根据“同位角相等,两直线平行”,
所以 ∥ .
根据“ ”,
所以∠1=∠EBG.
因为∠1+∠2=180°,所以∠EBG+∠2=180°.
根据“ ”,
所以EB∥DG.
根据“ ”,
所以∠GDE=∠BEA.
因为GD⊥AC,所以 =90°.所以∠BEA=90°.
因为∠AEF=65°,所以∠1= - =90°-65°=25°.
21.(10分)如图16,已知直线AB,CD,EF相交于点O,OG⊥CD,∠BOD=24°.
(1)求∠AOG的度数;
(2)若OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?说明你的理由.
图16
22.(12分)如图17,已知AM∥BN,∠A=64°,点是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②因为AM∥BN,所以∠ACB= ;
(2)求∠CBD的度数;
(3)当点运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关
系,并说明理由;若变化,请写出变化规律;
(4)当点运动到使∠ACB=∠ABD时,∠ABC的度数是 .
图17
附加题(共20分,不计入总分)
1.(6分)把一副三角尺按图1所示的方式摆放,点E在边AC上,将图中的三角形ABC绕点A按每秒3°
的速度沿顺时针方向旋转一周,在旋转的过程中,在第 秒时,边BC恰好与边DE平行.
图1
2.(14分)如图2,已知AB∥CD,∠B=30°,∠D=120°.
(1)如图①,若∠E=60°,则∠F=__________°.
(2)如图①,请探索∠E与∠F之间满足什么数量关系?并说明理由;
(3)如图②,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
第二章 相交线与平行线综合测评(一)
一、1. A 2. A 3. D 4. B 5. C 6. A 7. D 8. B 9. B 10. D
二、11. 110° 12. 4
13. 答案不唯一,如∠AOE=∠C,∠COE=115°等
14. 30° 15. 80°
16. 150° 提示:如图1,过点B作长方形一边的平行线.
因为长方形对边平行,所以∠1+∠ABD=180°,∠2+∠CBD=180°.所以∠1+∠ABC+∠2=360°.
因为AB⊥BC,所以∠ABC=90°,所以∠2=360°-120°-90°=150°.
图1
三、17. 解:如图2,用尺规作∠DCE=∠A,CD即为所求.
图2
18. 解:AE∥CD. 理由如下:
因为AB⊥CD,所以∠ABD=90°.
因为∠ABF=30°,所以∠FBD=∠ABD -∠ABF =90°-30°=60°.
因为∠FGE=60°,所以∠FBD=∠FGE.
根据“同位角相等,两直线平行”,
所以AE∥CD.
19. 解:因为AB∥CD,
根据“两直线平行,同旁内角互补”,
所以∠2+∠3=180°.
因为∠1=∠3,所以∠1+∠2=180°,即(4x-25)+(85-x)=180,解得x=40.
所以∠1=(4x-25)°=135°.
20. EF BC 两直线平行,内错角相等 同旁内角互补,两直线平行 两直线平行,同位角相等 ∠GDE
∠BEA ∠AEF
21. 解:(1)因为AB,CD相交于点O,所以∠AOC=∠BOD=24°.
因为OG⊥CD,所以∠COG=90°,即∠AOC+∠AOG=90°.
所以∠AOG=90°-∠AOC=90°-24°=66°.
(2)OG是∠AOF的平分线.
理由如下:因为OC是∠AOE的平分线,所以∠AOC=∠COE.
又因为∠DOF=∠COE,所以∠COA=∠DOF.
因为OG⊥CD,所以∠COG=∠DOG=90°.
所以∠AOG=∠GOF,所以OG平分∠AOF.
22. 解:(1)①116° ②∠CBN
(2)因为AM∥BN,所以∠ABN +∠A=180°,所以∠ABN=180°-∠A =180°-64°=116°,即∠ABP+
∠PBN=116°.
因为BC平分∠ABP,BD平分∠PBN,所以∠ABP=2∠CBP,∠PBN=2∠DBP.
所以2∠CBP+2∠DBP=116°,所以∠CBD=∠CBP+∠DBP=58°.
(3)不变,∠APB:∠ADB=2:1.理由如下:
因为AM∥BN,所以∠APB=∠PBN,∠ADB=∠DBN.
因为BD平分∠PBN,所以∠PBN=2∠DBN,所以∠APB =2∠ADB,即∠APB:∠ADB=2:1.
(4)29° 提示:因为AM∥BN,所以∠ACB=∠CBN.当∠ACB=∠ABD时,则有∠CBN=∠ABD.
所以∠ABC+∠CBD=∠CBD+∠DBN,所以∠ABC=∠DBN.
由(2)知∠CBD=58°.所以∠ABC+∠DBN=58°,所以∠ABC=29°.
附加题
1. 35或95 提示:如图1,当B′C′∥DE时.由题意,得∠DFA=∠B′=60°,∠D=45°,则∠FAD=75°.所以∠CAF=15°,∠BAF=105°.即BA绕点A顺时针旋转了105°.
故旋转的时间为:=35(秒).
图1 图2
如图2,当B″C″∥DE时.由(1)同理可得∠BAB″=75°,则BA绕点A顺时针旋转了360°-75°=285°.
故旋转的时间为:第=95(秒).
综上,在第35或95秒时,边BC恰好与边DE平行.
2. 解:(1)90°
(2)∠EFD=∠BEF+30°.理由:如图3,分别过点E,F作EM∥AB,FN∥AB,所以EM∥AB∥FN.所以∠B=∠BEM=30°,∠MEF=∠EFN.
又因为AB∥CD,AB∥FN,所以CD∥FN.所以∠D+∠DFN=180°.
又因为∠D=120°,所以∠DFN=60°.所以∠BEF=∠MEF+30°,∠EFD=∠EFN+60°.
所以∠EFD=∠MEF+60°.所以.
(3)如图4,过点F作FH∥EP,由(2)知∠EFD=∠BEF+30°.
设∠BEF=2x°,则∠EFD=(2x+30)°.
因为EP平分∠BEF,FG平分∠EFD,所以∠PEF=∠BEF=x°,∠EFG=∠EFD=(x+15)°.
因为FH∥EP,所以∠PEF=∠EFH=x°,∠P=∠HFG.
因为∠HFG=∠EFG-∠EFH=15°,所以∠P=15°.
_21?????????è?????(www.21cnjy.com)_
第二章 相交线与平行线综合测评(一)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 如图1,直线a,b被直线c所截,则∠1与∠2的位置关系是( )
A. 同位角 B. 内错角 C. 同旁内角 D. 互为补角
图1
2. 已知∠A与∠B互余,若∠A=60°,则∠B的度数为( )
A.30° B.60° C.120° D.150°
3. 在平面内,到直线l的距离等于2 cm的点有( )
A. 0个 B. 2个 C. 3个 D. 无数个
4. 下列四个图中,∠1=∠2一定成立的是( )
A B C D
5. 如图2,直线a,b被直线c所截,下列条件一定能判定直线a∥b的是( )
A.∠1=∠3 B.∠1=∠4 C.∠2=∠3 D.∠2+∠4=180°
图2 图3 图4 图5
6. 如图3,直线a,b相交于点O,如果∠1+∠2=110°,那么∠3的度数是( )
A. 125° B. 110° C. 70° D. 55°
7. 一把直尺与一把含有30°角的直角三角尺按图4所示的方式放置,若∠1=45°,则∠2的度数为( )
A. 45° B. 60° C. 65° D. 75°
8. 如图5,已知AB∥CD,若∠A=60°,∠ECD=120°,则∠ECA的度数是( )
A. 90° B. 120° C. 135° D. 150°
9.有下列说法:
①在同一平面内,两条直线的位置关系有平行、相交、垂直三种;
②平面内,过一点有且只有一条直线与已知直线垂直;
③过直线外一点有且只有一条直线与已知直线平行;
④同角或等角的补角相等.
其中正确的说法有( )
A.4?个 B.3?个 C.2?个 D.1?个
10. 如图6,有下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE,且∠ADC=∠B;④AB∥CE,且∠BCD=
∠BAD. 其中能推出BC∥AD的条件为( )
A. ①② B. ①②④ C. ①②③ D. ②③④
图6
二、填空题(本大题共6小题,每小题3分,共18分)
11. 若α=70°,则α的补角的度数是__________.
12. 如图7,已知AB⊥l1,AC⊥l2,若AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
图7 图8 图9 图10 图11
如图8,射线CA与直线BE交于点O,已知∠C=65°,请你添加一个条件__________________ ,使得BE∥CD.
14. 如图9,已知AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如
图所示的方式摆放,若∠EMB=75°,则∠PNM= .
15. 如图10,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BON=50°,则∠BOD的度数为_________.
16. 如图11,按虚线剪去长方形纸片(长方形的对边分别平行)的相邻两个角,并使∠1=120°,AB⊥BC,
那么∠2的度数为 .
三、解答题(本大题共6小题,共52分)
17.(6分)如图12,AB是某条河上的一座桥,现要在河的下游点C处再建一座与AB平行的桥CD,请用直尺和圆规画出CD的方向.
图12
18.(8分)如图13,已知AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,∠ABF=30°,请判断AE
与CD是否平行,并说明理由.
图13
19.(8分)如图14,已知AB∥CD,∠1 = (4x-25)°, ∠2 = (85-x)°, 求∠1的度数.
图14
20.(8分)如图15,在三角形ABC中,GD⊥AC于点D,∠AFE=∠ABC,
∠1+∠2=180°,∠AEF=65°,求∠1的度数. 将下列解答过程补充完整:
解:因为∠AFE=∠ABC,
根据“同位角相等,两直线平行”,
所以 ∥ .
根据“ ”,
所以∠1=∠EBG.
因为∠1+∠2=180°,所以∠EBG+∠2=180°.
根据“ ”,
所以EB∥DG.
根据“ ”,
所以∠GDE=∠BEA.
因为GD⊥AC,所以 =90°.所以∠BEA=90°.
因为∠AEF=65°,所以∠1= - =90°-65°=25°.
21.(10分)如图16,已知直线AB,CD,EF相交于点O,OG⊥CD,∠BOD=24°.
(1)求∠AOG的度数;
(2)若OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?说明你的理由.
图16
22.(12分)如图17,已知AM∥BN,∠A=64°,点是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②因为AM∥BN,所以∠ACB= ;
(2)求∠CBD的度数;
(3)当点运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关
系,并说明理由;若变化,请写出变化规律;
(4)当点运动到使∠ACB=∠ABD时,∠ABC的度数是 .
图17
附加题(共20分,不计入总分)
1.(6分)把一副三角尺按图1所示的方式摆放,点E在边AC上,将图中的三角形ABC绕点A按每秒3°
的速度沿顺时针方向旋转一周,在旋转的过程中,在第 秒时,边BC恰好与边DE平行.
图1
2.(14分)如图2,已知AB∥CD,∠B=30°,∠D=120°.
(1)如图①,若∠E=60°,则∠F=__________°.
(2)如图①,请探索∠E与∠F之间满足什么数量关系?并说明理由;
(3)如图②,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
第二章 相交线与平行线综合测评(一)
一、1. A 2. A 3. D 4. B 5. C 6. A 7. D 8. B 9. B 10. D
二、11. 110° 12. 4
13. 答案不唯一,如∠AOE=∠C,∠COE=115°等
14. 30° 15. 80°
16. 150° 提示:如图1,过点B作长方形一边的平行线.
因为长方形对边平行,所以∠1+∠ABD=180°,∠2+∠CBD=180°.所以∠1+∠ABC+∠2=360°.
因为AB⊥BC,所以∠ABC=90°,所以∠2=360°-120°-90°=150°.
图1
三、17. 解:如图2,用尺规作∠DCE=∠A,CD即为所求.
图2
18. 解:AE∥CD. 理由如下:
因为AB⊥CD,所以∠ABD=90°.
因为∠ABF=30°,所以∠FBD=∠ABD -∠ABF =90°-30°=60°.
因为∠FGE=60°,所以∠FBD=∠FGE.
根据“同位角相等,两直线平行”,
所以AE∥CD.
19. 解:因为AB∥CD,
根据“两直线平行,同旁内角互补”,
所以∠2+∠3=180°.
因为∠1=∠3,所以∠1+∠2=180°,即(4x-25)+(85-x)=180,解得x=40.
所以∠1=(4x-25)°=135°.
20. EF BC 两直线平行,内错角相等 同旁内角互补,两直线平行 两直线平行,同位角相等 ∠GDE
∠BEA ∠AEF
21. 解:(1)因为AB,CD相交于点O,所以∠AOC=∠BOD=24°.
因为OG⊥CD,所以∠COG=90°,即∠AOC+∠AOG=90°.
所以∠AOG=90°-∠AOC=90°-24°=66°.
(2)OG是∠AOF的平分线.
理由如下:因为OC是∠AOE的平分线,所以∠AOC=∠COE.
又因为∠DOF=∠COE,所以∠COA=∠DOF.
因为OG⊥CD,所以∠COG=∠DOG=90°.
所以∠AOG=∠GOF,所以OG平分∠AOF.
22. 解:(1)①116° ②∠CBN
(2)因为AM∥BN,所以∠ABN +∠A=180°,所以∠ABN=180°-∠A =180°-64°=116°,即∠ABP+
∠PBN=116°.
因为BC平分∠ABP,BD平分∠PBN,所以∠ABP=2∠CBP,∠PBN=2∠DBP.
所以2∠CBP+2∠DBP=116°,所以∠CBD=∠CBP+∠DBP=58°.
(3)不变,∠APB:∠ADB=2:1.理由如下:
因为AM∥BN,所以∠APB=∠PBN,∠ADB=∠DBN.
因为BD平分∠PBN,所以∠PBN=2∠DBN,所以∠APB =2∠ADB,即∠APB:∠ADB=2:1.
(4)29° 提示:因为AM∥BN,所以∠ACB=∠CBN.当∠ACB=∠ABD时,则有∠CBN=∠ABD.
所以∠ABC+∠CBD=∠CBD+∠DBN,所以∠ABC=∠DBN.
由(2)知∠CBD=58°.所以∠ABC+∠DBN=58°,所以∠ABC=29°.
附加题
1. 35或95 提示:如图1,当B′C′∥DE时.由题意,得∠DFA=∠B′=60°,∠D=45°,则∠FAD=75°.所以∠CAF=15°,∠BAF=105°.即BA绕点A顺时针旋转了105°.
故旋转的时间为:=35(秒).
图1 图2
如图2,当B″C″∥DE时.由(1)同理可得∠BAB″=75°,则BA绕点A顺时针旋转了360°-75°=285°.
故旋转的时间为:第=95(秒).
综上,在第35或95秒时,边BC恰好与边DE平行.
2. 解:(1)90°
(2)∠EFD=∠BEF+30°.理由:如图3,分别过点E,F作EM∥AB,FN∥AB,所以EM∥AB∥FN.所以∠B=∠BEM=30°,∠MEF=∠EFN.
又因为AB∥CD,AB∥FN,所以CD∥FN.所以∠D+∠DFN=180°.
又因为∠D=120°,所以∠DFN=60°.所以∠BEF=∠MEF+30°,∠EFD=∠EFN+60°.
所以∠EFD=∠MEF+60°.所以.
(3)如图4,过点F作FH∥EP,由(2)知∠EFD=∠BEF+30°.
设∠BEF=2x°,则∠EFD=(2x+30)°.
因为EP平分∠BEF,FG平分∠EFD,所以∠PEF=∠BEF=x°,∠EFG=∠EFD=(x+15)°.
因为FH∥EP,所以∠PEF=∠EFH=x°,∠P=∠HFG.
因为∠HFG=∠EFG-∠EFH=15°,所以∠P=15°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
