2021-2022学年青岛版八年级数学上册 2.5角平分线的性质 综合解答题培优提升专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学上册 2.5角平分线的性质 综合解答题培优提升专题训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 309.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 18:09:28 | ||
图片预览




文档简介
2021-2022学年青岛版八年级数学上册《2.5角平分线的性质》综合解答题
培优提升专题训练(附答案)
1.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
2.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28cm2,AB=16cm,AC=12cm,求DE的长.
3.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD于点F.求证:DE=BF.
4.在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
5.如图,AP,CP分别是△ABC外角∠MAC和∠NCA的平分线,它们交于点P.求证:BP为∠MBN的平分线.
6.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC于G,请猜测AE与FG之间有怎样的关系,并说明理由.
7.如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AB=AC.
求证:AD平分∠BAC.
8.如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.
9.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=54°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
10.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
11.如图所示,∠A=∠B=90°,P是AB的中点,且DP平分∠ADC,连接PC.
(1)求证:CP平分∠BCD;
(2)线段PD与PC有怎样的位置关系?请说明理由.
12.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC平分∠ABF,BF=AE.
求证:(1)DE=DF;
(2)AC=3BF.
13.如图,已知四边形ABCD中,∠ABC与∠BCD的平分线交于点O,作OE⊥AB于点E,OF⊥CD于点F.求证:OE=OF.
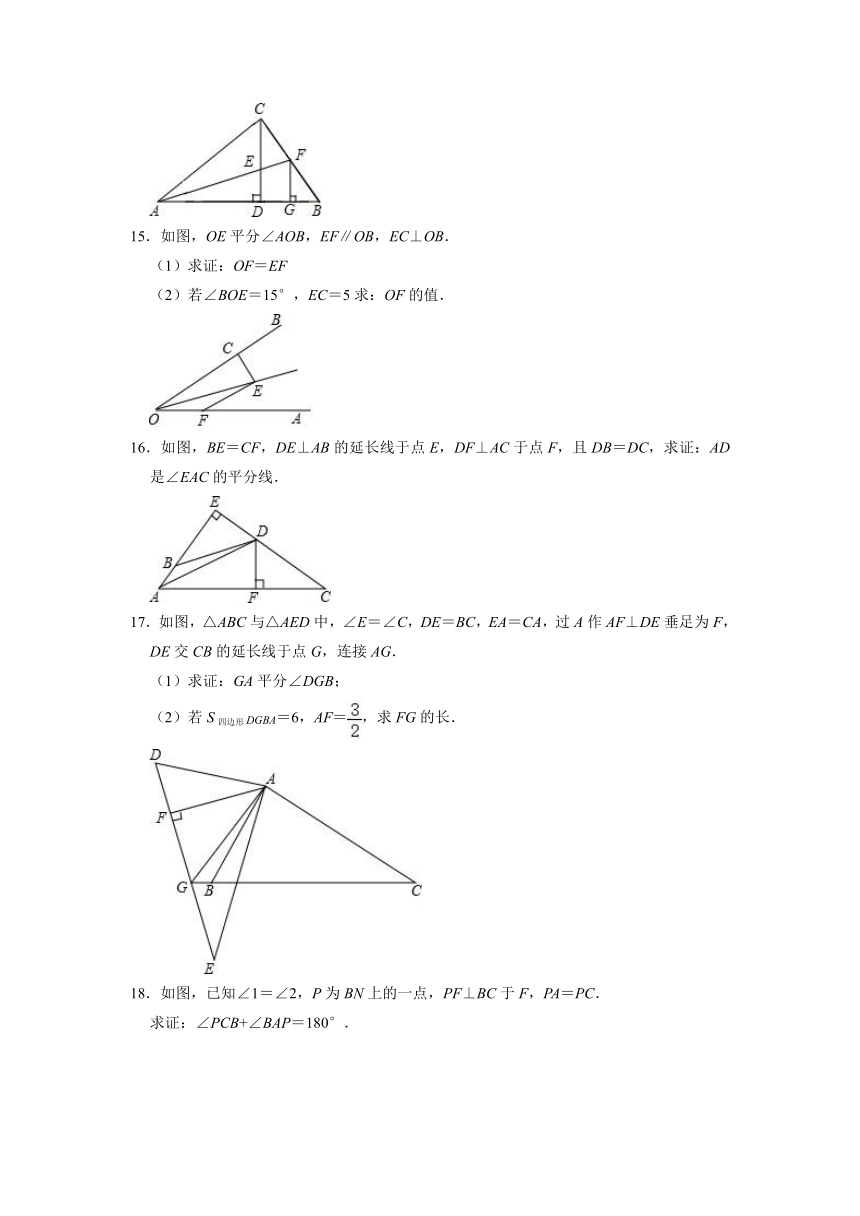
14.如图,CD为△ABC斜边上的高,∠BAC的平分线分别交CD,BC于点E、F,FG⊥AB,垂足为点G.求证:CE=FG.
15.如图,OE平分∠AOB,EF∥OB,EC⊥OB.
(1)求证:OF=EF
(2)若∠BOE=15°,EC=5求:OF的值.
16.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠EAC的平分线.
17.如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF=,求FG的长.
18.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC.
求证:∠PCB+∠BAP=180°.
19.已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.
求证:点O到EB与ED的距离相等.
20.(1)如图①,在Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,交BC于点D.如果作辅助线DE⊥AB于点E,则可以得到AC、CD、AB三条线段之间的数量关系为 ;
(2)如图,△ABC中,∠C=2∠B,AD平分∠BAC,交BC于点D.(1)中的结论是否仍然成立?若不成立,试说明理由;若成立,请证明.
参考答案
1.证明:(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB,
∴CF=EB;
(2)AF+BE=AE.
∵Rt△DCF≌Rt△DEB,
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
2.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF
∵S△ABC=S△ABD+S△ACD=AB×DE+AC×DF
∴S△ABC=(AB+AC)×DE,
即×(16+12)×DE=28,
∴DE=2(cm).
3.证明:∵CD平分∠ACB,
∴∠1=∠2,
∵∠1=∠2,DE⊥AC,∠ABC=90°
∴DE=BD,
∵∠3=90°﹣∠1,∠4=90°﹣∠2,
∴∠3=∠4,
∵BF∥DE,
∴∠4=∠5,
∴∠3=∠5,
∴BD=BF,
∴DE=BF.
4.解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
5.证明:过P作三边AB、AC、BC的垂线段PD、PE、PF,
∵AP是△ABC的外角平分线,PD⊥AD,PF⊥AC,
∴PD=PF(角平分线上的点到角两边的距离相等),
∵CP是△ABC的外角平分线,PE⊥AC,PF⊥BC,
∴PE=PF(角平分线上的点到角两边的距离相等),
又∵PD=PE,PD⊥AD,PE⊥AC,
∴AP为∠MBN的平分线(在角的内部,到角两边距离相等的点在角的平分线上).
6.解:AE=FG,AE∥FG.
理由如下:∵CF是∠ACB的平分线,∠BAC=90°,FG⊥BC,
∴FA=FG,∠AFC=∠CED,
∵∠AEF=∠CED,
∴∠AEF=∠AFC,
∴AE=AF,
∴AE=FG,
∵AD⊥BC,FG⊥BC,
∴AE∥FG,
∴AE=FG,AE∥FG.
7.解:方法一:连接BC,
∵BE⊥AC于E,CF⊥AB于F,
∴∠CFB=∠BEC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△BCF和△CBE中
∵
∴△BCF≌△CBE(AAS),
∴BF=CE,
在△BFD和△CED中
∵,
∴△BFD≌△CED(AAS),
∴DF=DE,
∴AD平分∠BAC.
方法二:先证△AFC≌△AEB,得到AE=AF,再用(HL)证△AFD≌△三AED,得到∠FAD=∠EAD,所以AD平分∠BAC.
8.解:PC与PD相等.理由如下:
过点P作PE⊥OA于点E,PF⊥OB于点F.
∵OM平分∠AOB,点P在OM上,PE⊥OA,PF⊥OB,
∴PE=PF(角平分线上的点到角两边的距离相等)
又∵∠AOB=90°,∠PEO=∠PFO=90°,
∴四边形OEPF为矩形,
∴∠EPF=90°,
∴∠EPC+∠CPF=90°,
又∵∠CPD=90°,
∴∠CPF+∠FPD=90°,
∴∠EPC=∠FPD=90°﹣∠CPF.
在△PCE与△PDF中,
∵,
∴△PCE≌△PDF(ASA),
∴PC=PD.
9.(1)解:∵∠BAC=54°,AD平分∠BAC,
∴∠EAD=∠BAC=27°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣27°=63°.
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,ED=DC,
∵AD平分∠BAC,
∴AD⊥CE,
∵AE=AC,ED=DC,
∴点D在CE的垂直平分线上,点A在CE的垂直平分线上,(两点确定一条直线),
∴直线AD是线段CE的垂直平分线.
即直线AD是线段CE的垂直平分线.
10.(1)证明:过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴=∠DEB+∠ABC,
∴∠DEB=(∠CDA﹣∠ABC)=∠BAD=30°.
11.(1)证明:过P作PQ⊥CD于Q,
∵P是AB的中点,
∴PA=PB,
∵DP平分∠ADC,∠A=90°,PQ⊥CD,
∴PA=PQ,
∴PA=PQ=PB,
∵∠B=90°,PQ⊥CD,
∴CP平分∠BCD;
(2)PD⊥PC,
证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DP平分∠ADC,CP平分∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠PDC+∠PCD=90°,
∴∠DPC=90°,
∴PD⊥PC.
12.解:(1)∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,
在△CDE与△BDF中,
,
∴△CDE≌△BDF,
∴DE=DF.
(2)∵△CDE≌△BDF,
∴CE=BF,
∵BF=AE,
∴AE=2BF,
∴AC=3BF.
13.证明:作OG⊥BC,
∵∠ABC的平分线,OE⊥AB,OG⊥BC,
∴OE=OG,
∵∠BCD的平分线,OF⊥CD,OG⊥BC,
∴OF=OG,
∴OE=OF.
14.证明:∵AF是∠BAC的平分线,∠ACB=90°,FG⊥AB,
∴FC=FG,∠AED=∠AFC,
∵∠AED=∠CEF,
∴∠CEF=∠AFC,
∴CE=CF,
∴CE=FG.
15.(1)证明:∵OE平分∠AOB,
∴∠BOE=∠AOE,
∵EF∥OB,
∴∠BOE=∠OEF,
∴∠OEF=∠FOE,
∴OF=EF;
(2)解:过E作ED⊥OA于D,
∵∠BOE=15°,
∴∠OEF=∠FOE=15°,
∴∠EFD=30°,
∵CE⊥OB,
∴DE=CE=5,
∴EF=2DE=10,
∴OF=EF=10.
16.证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD,
∴△BDE与△CDF是直角三角形,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴AD是∠BAC的平分线.
17.解:(1)过点A作AH⊥BC于H,
∵△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,
∴△ABC≌△ADE(SAS),
∴S△ABC=S△AED,
又∵AF⊥DE,
即×DE×AF=×BC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,AG=AG,
∴Rt△AFG≌Rt△AHG(HL),
∴∠AGF=∠AGH,
即GA平分∠DGB;
(2)∵△ABC≌△ADE,
∴AD=AB,
又∵AF⊥DE,AH⊥BC,AF=AH,
∴Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF=,
∴×FG×=3,
解得FG=4.
18.证明:如图,过点P作PE⊥BA于E,
∵∠1=∠2,PF⊥BC于F,
∴PE=PF,∠PEA=∠PFB=90°,
在Rt△PEA与Rt△PFC中,
∴Rt△PEA≌Rt△PFC(HL),
∴∠PAE=∠PCB,
∵∠BAP+∠PAE=180°,
∴∠PCB+∠BAP=180°.
19.证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,又CE平分∠BCD,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
20.解:(1)如图1,∵AD平分∠BAC,
∴∠CAD=∠EAD,
在△CAD和△EAD中
,
∴△CAD≌△EAD(AAS),
∴CD=DE,AC=AE,
∵∠B=45°,∠DEB=90°,
∴DE=EB,
∴DC=BE,
∴AE+BE=AC+DC=AB;
故答案为:AB=AC+CD.
(2)成立.
证明:如图2,在AB上截取AE=AC,连接DE.
∵在△ACD和△AED中
,
∴△ACD≌△AED(SAS),
∴CD=ED,∠C=∠AED,
又∵∠C=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴2∠B=∠B+∠EDB,
∴∠B=∠EDB,
∴ED=EB
∵AB=AE+EB,ED=EB=CD,AE=AC,
∴AB=AC+CD.
培优提升专题训练(附答案)
1.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
2.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28cm2,AB=16cm,AC=12cm,求DE的长.
3.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD于点F.求证:DE=BF.
4.在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
5.如图,AP,CP分别是△ABC外角∠MAC和∠NCA的平分线,它们交于点P.求证:BP为∠MBN的平分线.
6.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC于G,请猜测AE与FG之间有怎样的关系,并说明理由.
7.如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AB=AC.
求证:AD平分∠BAC.
8.如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.
9.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=54°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
10.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
11.如图所示,∠A=∠B=90°,P是AB的中点,且DP平分∠ADC,连接PC.
(1)求证:CP平分∠BCD;
(2)线段PD与PC有怎样的位置关系?请说明理由.
12.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC平分∠ABF,BF=AE.
求证:(1)DE=DF;
(2)AC=3BF.
13.如图,已知四边形ABCD中,∠ABC与∠BCD的平分线交于点O,作OE⊥AB于点E,OF⊥CD于点F.求证:OE=OF.
14.如图,CD为△ABC斜边上的高,∠BAC的平分线分别交CD,BC于点E、F,FG⊥AB,垂足为点G.求证:CE=FG.
15.如图,OE平分∠AOB,EF∥OB,EC⊥OB.
(1)求证:OF=EF
(2)若∠BOE=15°,EC=5求:OF的值.
16.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠EAC的平分线.
17.如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF=,求FG的长.
18.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC.
求证:∠PCB+∠BAP=180°.
19.已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.
求证:点O到EB与ED的距离相等.
20.(1)如图①,在Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,交BC于点D.如果作辅助线DE⊥AB于点E,则可以得到AC、CD、AB三条线段之间的数量关系为 ;
(2)如图,△ABC中,∠C=2∠B,AD平分∠BAC,交BC于点D.(1)中的结论是否仍然成立?若不成立,试说明理由;若成立,请证明.
参考答案
1.证明:(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB,
∴CF=EB;
(2)AF+BE=AE.
∵Rt△DCF≌Rt△DEB,
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
2.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF
∵S△ABC=S△ABD+S△ACD=AB×DE+AC×DF
∴S△ABC=(AB+AC)×DE,
即×(16+12)×DE=28,
∴DE=2(cm).
3.证明:∵CD平分∠ACB,
∴∠1=∠2,
∵∠1=∠2,DE⊥AC,∠ABC=90°
∴DE=BD,
∵∠3=90°﹣∠1,∠4=90°﹣∠2,
∴∠3=∠4,
∵BF∥DE,
∴∠4=∠5,
∴∠3=∠5,
∴BD=BF,
∴DE=BF.
4.解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
5.证明:过P作三边AB、AC、BC的垂线段PD、PE、PF,
∵AP是△ABC的外角平分线,PD⊥AD,PF⊥AC,
∴PD=PF(角平分线上的点到角两边的距离相等),
∵CP是△ABC的外角平分线,PE⊥AC,PF⊥BC,
∴PE=PF(角平分线上的点到角两边的距离相等),
又∵PD=PE,PD⊥AD,PE⊥AC,
∴AP为∠MBN的平分线(在角的内部,到角两边距离相等的点在角的平分线上).
6.解:AE=FG,AE∥FG.
理由如下:∵CF是∠ACB的平分线,∠BAC=90°,FG⊥BC,
∴FA=FG,∠AFC=∠CED,
∵∠AEF=∠CED,
∴∠AEF=∠AFC,
∴AE=AF,
∴AE=FG,
∵AD⊥BC,FG⊥BC,
∴AE∥FG,
∴AE=FG,AE∥FG.
7.解:方法一:连接BC,
∵BE⊥AC于E,CF⊥AB于F,
∴∠CFB=∠BEC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△BCF和△CBE中
∵
∴△BCF≌△CBE(AAS),
∴BF=CE,
在△BFD和△CED中
∵,
∴△BFD≌△CED(AAS),
∴DF=DE,
∴AD平分∠BAC.
方法二:先证△AFC≌△AEB,得到AE=AF,再用(HL)证△AFD≌△三AED,得到∠FAD=∠EAD,所以AD平分∠BAC.
8.解:PC与PD相等.理由如下:
过点P作PE⊥OA于点E,PF⊥OB于点F.
∵OM平分∠AOB,点P在OM上,PE⊥OA,PF⊥OB,
∴PE=PF(角平分线上的点到角两边的距离相等)
又∵∠AOB=90°,∠PEO=∠PFO=90°,
∴四边形OEPF为矩形,
∴∠EPF=90°,
∴∠EPC+∠CPF=90°,
又∵∠CPD=90°,
∴∠CPF+∠FPD=90°,
∴∠EPC=∠FPD=90°﹣∠CPF.
在△PCE与△PDF中,
∵,
∴△PCE≌△PDF(ASA),
∴PC=PD.
9.(1)解:∵∠BAC=54°,AD平分∠BAC,
∴∠EAD=∠BAC=27°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣27°=63°.
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,ED=DC,
∵AD平分∠BAC,
∴AD⊥CE,
∵AE=AC,ED=DC,
∴点D在CE的垂直平分线上,点A在CE的垂直平分线上,(两点确定一条直线),
∴直线AD是线段CE的垂直平分线.
即直线AD是线段CE的垂直平分线.
10.(1)证明:过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴=∠DEB+∠ABC,
∴∠DEB=(∠CDA﹣∠ABC)=∠BAD=30°.
11.(1)证明:过P作PQ⊥CD于Q,
∵P是AB的中点,
∴PA=PB,
∵DP平分∠ADC,∠A=90°,PQ⊥CD,
∴PA=PQ,
∴PA=PQ=PB,
∵∠B=90°,PQ⊥CD,
∴CP平分∠BCD;
(2)PD⊥PC,
证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DP平分∠ADC,CP平分∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠PDC+∠PCD=90°,
∴∠DPC=90°,
∴PD⊥PC.
12.解:(1)∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,
在△CDE与△BDF中,
,
∴△CDE≌△BDF,
∴DE=DF.
(2)∵△CDE≌△BDF,
∴CE=BF,
∵BF=AE,
∴AE=2BF,
∴AC=3BF.
13.证明:作OG⊥BC,
∵∠ABC的平分线,OE⊥AB,OG⊥BC,
∴OE=OG,
∵∠BCD的平分线,OF⊥CD,OG⊥BC,
∴OF=OG,
∴OE=OF.
14.证明:∵AF是∠BAC的平分线,∠ACB=90°,FG⊥AB,
∴FC=FG,∠AED=∠AFC,
∵∠AED=∠CEF,
∴∠CEF=∠AFC,
∴CE=CF,
∴CE=FG.
15.(1)证明:∵OE平分∠AOB,
∴∠BOE=∠AOE,
∵EF∥OB,
∴∠BOE=∠OEF,
∴∠OEF=∠FOE,
∴OF=EF;
(2)解:过E作ED⊥OA于D,
∵∠BOE=15°,
∴∠OEF=∠FOE=15°,
∴∠EFD=30°,
∵CE⊥OB,
∴DE=CE=5,
∴EF=2DE=10,
∴OF=EF=10.
16.证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD,
∴△BDE与△CDF是直角三角形,
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴AD是∠BAC的平分线.
17.解:(1)过点A作AH⊥BC于H,
∵△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,
∴△ABC≌△ADE(SAS),
∴S△ABC=S△AED,
又∵AF⊥DE,
即×DE×AF=×BC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,AG=AG,
∴Rt△AFG≌Rt△AHG(HL),
∴∠AGF=∠AGH,
即GA平分∠DGB;
(2)∵△ABC≌△ADE,
∴AD=AB,
又∵AF⊥DE,AH⊥BC,AF=AH,
∴Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF=,
∴×FG×=3,
解得FG=4.
18.证明:如图,过点P作PE⊥BA于E,
∵∠1=∠2,PF⊥BC于F,
∴PE=PF,∠PEA=∠PFB=90°,
在Rt△PEA与Rt△PFC中,
∴Rt△PEA≌Rt△PFC(HL),
∴∠PAE=∠PCB,
∵∠BAP+∠PAE=180°,
∴∠PCB+∠BAP=180°.
19.证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,又CE平分∠BCD,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
20.解:(1)如图1,∵AD平分∠BAC,
∴∠CAD=∠EAD,
在△CAD和△EAD中
,
∴△CAD≌△EAD(AAS),
∴CD=DE,AC=AE,
∵∠B=45°,∠DEB=90°,
∴DE=EB,
∴DC=BE,
∴AE+BE=AC+DC=AB;
故答案为:AB=AC+CD.
(2)成立.
证明:如图2,在AB上截取AE=AC,连接DE.
∵在△ACD和△AED中
,
∴△ACD≌△AED(SAS),
∴CD=ED,∠C=∠AED,
又∵∠C=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴2∠B=∠B+∠EDB,
∴∠B=∠EDB,
∴ED=EB
∵AB=AE+EB,ED=EB=CD,AE=AC,
∴AB=AC+CD.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
