人教版2022年七年级下册:5.3《平行线的性质》 同步练习卷(word版,含详解)
文档属性
| 名称 | 人教版2022年七年级下册:5.3《平行线的性质》 同步练习卷(word版,含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览



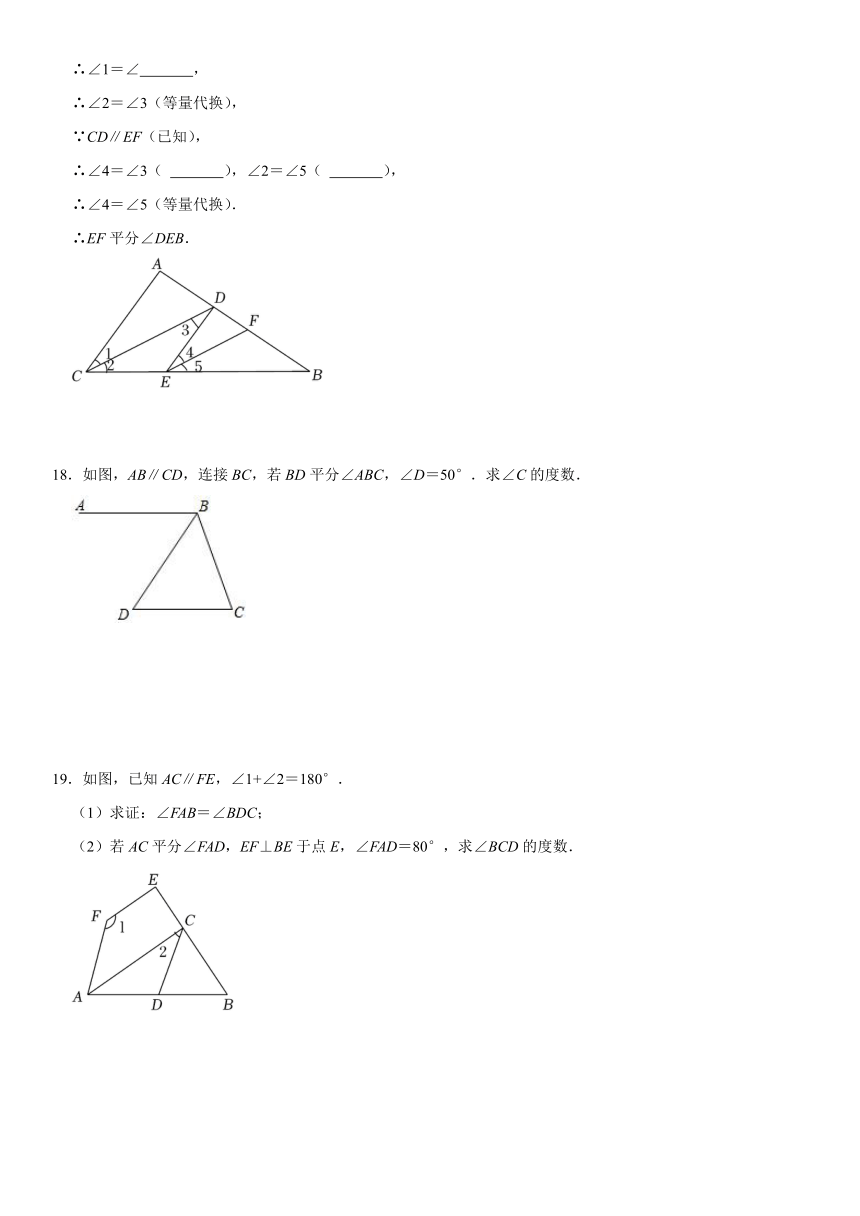
文档简介
人教版2022年七年级下册:5.3《平行线的性质》 同步练习卷
一.选择题
1.如图,若a∥b,∠1=60°27′,则∠2等于( )
A.60°27′ B.60°73′ C.119°33′ D.119°73′
2.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.同旁内角互补
C.等角的补角相等 D.垂线段最短
3.如图,若要使l1与l2平行,则l1绕点O至少旋转的度数是( )
A.38° B.42° C.80° D.138°
4.如图,如果∠1=∠3,∠2=50°,那么∠4的度数为( )
A.50° B.100° C.120° D.130°
5.如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=40°,则∠2=( )
A.40° B.50° C.60° D.70°
6.如图,在长方形ABCD纸片中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C、D分别落在C'、D'的位置.若∠EFB=65°,则∠AED'等于( )
A.70° B.65° C.50° D.25°
二.填空题
7.把下面的命题改写成“如果…,那么…”形式:内错角相等,两直线平行 .
8.如图,AB∥CD且被直线AE所截,∠1=80°,则∠2的度数是 .
9.如图,AB∥CD,AD⊥AC,∠BAD=40°,则∠ACD等于 °.
10.如图,一辆汽车经过两次转弯后,行驶的方向与原来保持平行,如果第一次转过的角α为64°,则第二次转过的角β为 °.
11.如图,AB∥CD,∠A=25°,∠E=80°,则∠C的度数是 .
12.在平面内,若∠A与∠B的两边分别平行,∠A=60°,则∠B= .
13.如图,已知AB∥CD,则∠A、∠C、∠P的关系为 .
14.把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论:①∠C'EF=32°;②∠AEC=1480';③∠BGE=64°;④∠BFD=116°.正确的有 个.
三.解答题
15.如图,∠B=∠BGD,∠BGC=∠F.试说明∠B+∠F=180°.请完善解答过程,并在括号内填写相应的理论根据.
解:∵∠B=∠BGD(已知),
∴ ∥CD( ).
∵∠BGC=∠F(已知),
∴CD∥ ( ).
∴ ∥ (平行于同一直线的两直线平行).
∴∠B+∠F=180°( ).
16.如图,已知AB⊥AC,DE⊥AC,∠B=∠D.试说明:AD∥BC.
在下列解答中,填上适当的理由或数学式.
解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴ =∠DEC( ).
又∵∠B=∠D(已知),
∴∠D= (等量代换),
∴AD∥BC( ).
17.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,那么EF平分∠DEB吗?
解:∵CD平分∠ACB(已知),
∴∠1=∠2( ),
∵AC∥DE(已知),
∴∠1=∠ ,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3( ),∠2=∠5( ),
∴∠4=∠5(等量代换).
∴EF平分∠DEB.
18.如图,AB∥CD,连接BC,若BD平分∠ABC,∠D=50°.求∠C的度数.
19.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
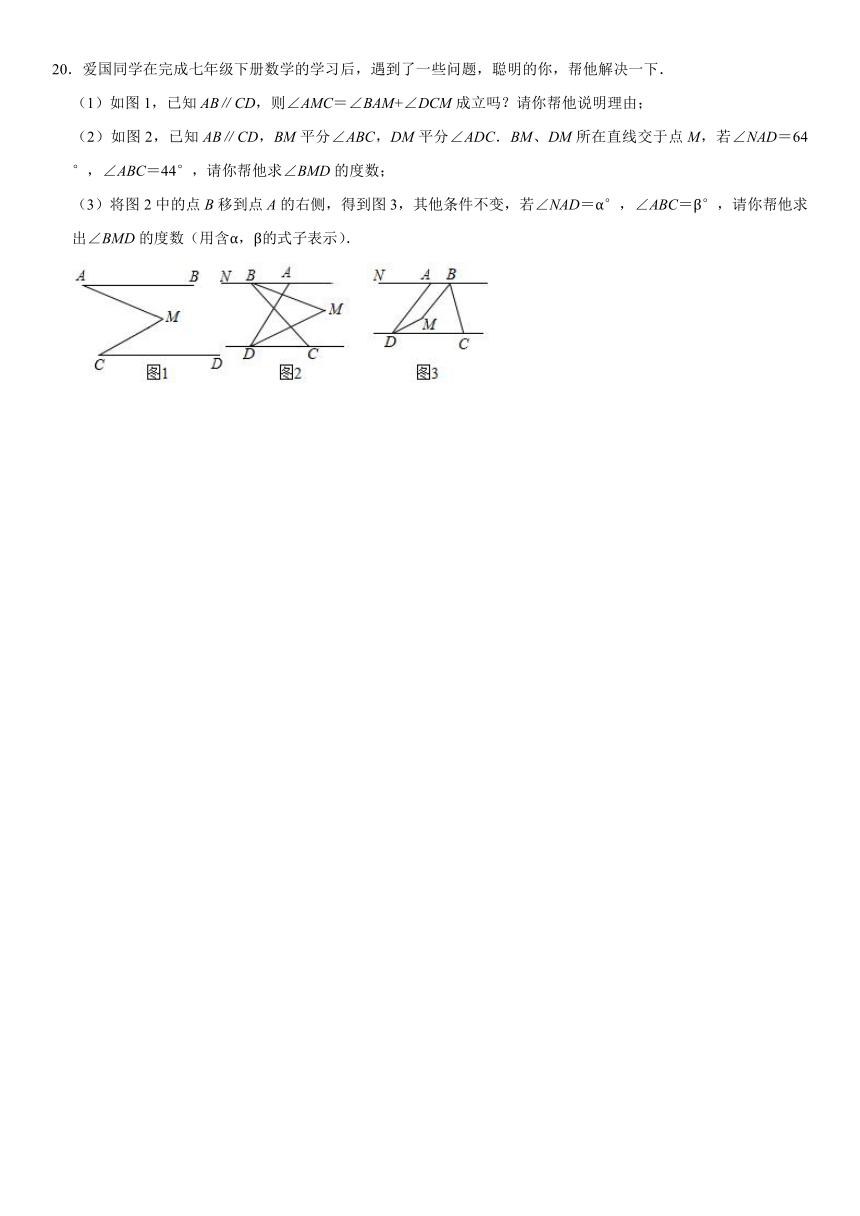
20.爱国同学在完成七年级下册数学的学习后,遇到了一些问题,聪明的你,帮他解决一下.
(1)如图1,已知AB∥CD,则∠AMC=∠BAM+∠DCM成立吗?请你帮他说明理由;
(2)如图2,已知AB∥CD,BM平分∠ABC,DM平分∠ADC.BM、DM所在直线交于点M,若∠NAD=64°,∠ABC=44°,请你帮他求∠BMD的度数;
(3)将图2中的点B移到点A的右侧,得到图3,其他条件不变,若∠NAD=α°,∠ABC=β°,请你帮他求出∠BMD的度数(用含α,β的式子表示).
参考答案
一.选择题
1.解:如图,
由题意得∠3=180°﹣∠1=119°33',
∵a∥b,
∴∠2=∠3=119°33',
故选:C.
2.解:A、两点之间,线段最短,是真命题;
B、两直线平行,同旁内角互补,原命题是假命题;
C、等角的补角相等,是真命题;
D、垂线段最短,是真命题;
故选:B.
3.解:若l1与l2平行,
则∠1和∠2相等,
∵∠2=42°,
∴∠1=42°,
∴若要使l1与l2平行,则l1绕点O至少旋转的度数是80°﹣42°=38°,
故选:A.
4.解:如图,
∵∠1=∠3,
∴a∥b,
∴∠5=∠2=50°,
∴∠4=180°﹣50°=130°.
故选:D.
5.解:根据题意可知,
∠1=∠3=40°,
∵∠3+∠4=90°,
∴∠4=90°﹣40°=50°,
∴∠2=∠4=50°.
故选:B.
6.解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠DEF=∠EFB=65°,
又由折叠的性质可得∠D′EF=∠DEF=65°,
∴∠AED′=180°﹣65°﹣65°=50°,
故选:C.
二.填空题
7.解:将命题:内错角相等,两直线平行改写成“如果…,那么…”形式:如果内错角相等,那么两直线平行,
故答案为:如果内错角相等,那么两直线平行.
8.解:∵∠1=80°,∠1+∠3=180°,
∴∠3=100°,
∵AB∥CD,
∴∠2=∠3=100°.
故答案为:100°.
9.解:∵AD⊥AC,
∴∠CAD=90°,
∵∠BAD=40°,
∴∠BAC=∠CAD+∠BAD=130°,
∵AB∥CD,
∴∠ACD+∠BAC=180°,
∴∠ACD=180°﹣∠BAC=50°.
故答案为:50.
10.解:∵∠α=64°,
∴∠BAC=180°﹣∠α=116°,
∵AB∥CD,
∴∠β=∠BAC=116°,
故答案为:116.
11.解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠AEF=∠A=25°,∠CEF=∠C,
又∵∠AEC=80°,
∴∠C=∠CEF=80°﹣25°=55°.
故答案为:55°.
12.解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=60°,
∴∠B=60°,或∠B=180°﹣∠A=180°﹣60°=120°.
故答案为:60°或120°.
13.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
14.解:∵AC′∥BD′,
∴∠C′EF=∠EFB=32°,所以①正确;
∵∠C′EF=∠FEC,
∴∠C′EC=2×32°=64°,
∴∠AEC=180°﹣64°=116°=6960′,所以②错误;
∴∠BFD=∠EFD′﹣∠BFE=180°﹣2∠EFB=180°﹣64°=116°,所以④正确;
∵∠BGE=∠C′EC=2×32°=64°,所以③正确.
故答案为3.
三.解答题
15.解:∵∠B=∠BGD(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠BGC=∠F(已知),
∴CD∥EF(同位角相等,两直线平行).
∴AB∥EF(平行于同一直线的两直线平行).
∴∠B+∠F=180°(两直线平行,同旁内角互补).
故答案为:AB;内错角相等,两直线平行;EF;同位角相等,两直线平行;AB;EF;两直线平行,同旁内角互补.
16.解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴∠B=∠DEC(两直线平行,同位角相等).
又∵∠B=∠D(已知),
∴∠D=∠DEC(等量代换),
∴AD∥BC(内错角相等,两直线平行)、
故答案为:∠B,两直线平行,同位角相等,∠DEC,内错角相等,两直线平行.
17.解:∵CD平分∠ACB(已知),
∴∠1=∠2(角平分线的定义),
∵AC∥DE(已知),
∴∠1=∠3,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3(两直线平行,内错角相等),∠2=∠5(两直线平行,同位角相等),
∴∠4=∠5(等量代换).
故答案为:角平分线的定义;3;两直线平行,内错角相等;两直线平行,同位角相等.
18.解:∵AB∥CD,
∴∠ABD=∠D=50°,∠ABC+∠C=180°.
∵BD平分∠ABC,
∴∠ABC=2∠ABD=100°.
∴∠C=180°﹣∠ABC
=180°﹣100°
=80°.
19.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
20.解:(1)成立,
理由:如图1中,作MN∥AB,则有MN∥CD,
∴∠1=∠BAM,∠2=∠DCM,
∴∠AMC=∠1+∠2=∠BAM+∠DCM.
(2)如图2,过点M作MH∥AB,
∵AB∥CD,∠NAD=64°,
∴∠NAD=∠ADC=64°,
∵DM平分∠ADC,∠ADC=64°,
∴∠MDC=∠ADC=32°,
∵BM平分∠ABC,∠ABC=44°,
∴∠ABM=∠ABC=22°,
∵AB∥CD,
∴AB∥CD∥MH,
∴∠ABM=∠BMH=22°,∠CDM=∠DMH=32°,
∴∠BMD=∠BMH+∠DMH=54°.
(3)如图3,过点M作MG∥AB,
∵BM平分∠ABC,DM平分∠ADC,∠ABC=β°,∠ADC=∠BAD=α°,
∴∠ABM=∠ABC=β°,∠CDM=∠ADC=α°,
∵AB∥CD,
∴AB∥CD∥MG,
∴∠BMG=180°﹣∠ABM=180°﹣β°,∠CDM=∠DMG=α°,
∴∠BMD=∠BMG+∠DMG=180°﹣β°+α°.
一.选择题
1.如图,若a∥b,∠1=60°27′,则∠2等于( )
A.60°27′ B.60°73′ C.119°33′ D.119°73′
2.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.同旁内角互补
C.等角的补角相等 D.垂线段最短
3.如图,若要使l1与l2平行,则l1绕点O至少旋转的度数是( )
A.38° B.42° C.80° D.138°
4.如图,如果∠1=∠3,∠2=50°,那么∠4的度数为( )
A.50° B.100° C.120° D.130°
5.如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=40°,则∠2=( )
A.40° B.50° C.60° D.70°
6.如图,在长方形ABCD纸片中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C、D分别落在C'、D'的位置.若∠EFB=65°,则∠AED'等于( )
A.70° B.65° C.50° D.25°
二.填空题
7.把下面的命题改写成“如果…,那么…”形式:内错角相等,两直线平行 .
8.如图,AB∥CD且被直线AE所截,∠1=80°,则∠2的度数是 .
9.如图,AB∥CD,AD⊥AC,∠BAD=40°,则∠ACD等于 °.
10.如图,一辆汽车经过两次转弯后,行驶的方向与原来保持平行,如果第一次转过的角α为64°,则第二次转过的角β为 °.
11.如图,AB∥CD,∠A=25°,∠E=80°,则∠C的度数是 .
12.在平面内,若∠A与∠B的两边分别平行,∠A=60°,则∠B= .
13.如图,已知AB∥CD,则∠A、∠C、∠P的关系为 .
14.把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论:①∠C'EF=32°;②∠AEC=1480';③∠BGE=64°;④∠BFD=116°.正确的有 个.
三.解答题
15.如图,∠B=∠BGD,∠BGC=∠F.试说明∠B+∠F=180°.请完善解答过程,并在括号内填写相应的理论根据.
解:∵∠B=∠BGD(已知),
∴ ∥CD( ).
∵∠BGC=∠F(已知),
∴CD∥ ( ).
∴ ∥ (平行于同一直线的两直线平行).
∴∠B+∠F=180°( ).
16.如图,已知AB⊥AC,DE⊥AC,∠B=∠D.试说明:AD∥BC.
在下列解答中,填上适当的理由或数学式.
解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴ =∠DEC( ).
又∵∠B=∠D(已知),
∴∠D= (等量代换),
∴AD∥BC( ).
17.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,那么EF平分∠DEB吗?
解:∵CD平分∠ACB(已知),
∴∠1=∠2( ),
∵AC∥DE(已知),
∴∠1=∠ ,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3( ),∠2=∠5( ),
∴∠4=∠5(等量代换).
∴EF平分∠DEB.
18.如图,AB∥CD,连接BC,若BD平分∠ABC,∠D=50°.求∠C的度数.
19.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
20.爱国同学在完成七年级下册数学的学习后,遇到了一些问题,聪明的你,帮他解决一下.
(1)如图1,已知AB∥CD,则∠AMC=∠BAM+∠DCM成立吗?请你帮他说明理由;
(2)如图2,已知AB∥CD,BM平分∠ABC,DM平分∠ADC.BM、DM所在直线交于点M,若∠NAD=64°,∠ABC=44°,请你帮他求∠BMD的度数;
(3)将图2中的点B移到点A的右侧,得到图3,其他条件不变,若∠NAD=α°,∠ABC=β°,请你帮他求出∠BMD的度数(用含α,β的式子表示).
参考答案
一.选择题
1.解:如图,
由题意得∠3=180°﹣∠1=119°33',
∵a∥b,
∴∠2=∠3=119°33',
故选:C.
2.解:A、两点之间,线段最短,是真命题;
B、两直线平行,同旁内角互补,原命题是假命题;
C、等角的补角相等,是真命题;
D、垂线段最短,是真命题;
故选:B.
3.解:若l1与l2平行,
则∠1和∠2相等,
∵∠2=42°,
∴∠1=42°,
∴若要使l1与l2平行,则l1绕点O至少旋转的度数是80°﹣42°=38°,
故选:A.
4.解:如图,
∵∠1=∠3,
∴a∥b,
∴∠5=∠2=50°,
∴∠4=180°﹣50°=130°.
故选:D.
5.解:根据题意可知,
∠1=∠3=40°,
∵∠3+∠4=90°,
∴∠4=90°﹣40°=50°,
∴∠2=∠4=50°.
故选:B.
6.解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠DEF=∠EFB=65°,
又由折叠的性质可得∠D′EF=∠DEF=65°,
∴∠AED′=180°﹣65°﹣65°=50°,
故选:C.
二.填空题
7.解:将命题:内错角相等,两直线平行改写成“如果…,那么…”形式:如果内错角相等,那么两直线平行,
故答案为:如果内错角相等,那么两直线平行.
8.解:∵∠1=80°,∠1+∠3=180°,
∴∠3=100°,
∵AB∥CD,
∴∠2=∠3=100°.
故答案为:100°.
9.解:∵AD⊥AC,
∴∠CAD=90°,
∵∠BAD=40°,
∴∠BAC=∠CAD+∠BAD=130°,
∵AB∥CD,
∴∠ACD+∠BAC=180°,
∴∠ACD=180°﹣∠BAC=50°.
故答案为:50.
10.解:∵∠α=64°,
∴∠BAC=180°﹣∠α=116°,
∵AB∥CD,
∴∠β=∠BAC=116°,
故答案为:116.
11.解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠AEF=∠A=25°,∠CEF=∠C,
又∵∠AEC=80°,
∴∠C=∠CEF=80°﹣25°=55°.
故答案为:55°.
12.解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=60°,
∴∠B=60°,或∠B=180°﹣∠A=180°﹣60°=120°.
故答案为:60°或120°.
13.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
14.解:∵AC′∥BD′,
∴∠C′EF=∠EFB=32°,所以①正确;
∵∠C′EF=∠FEC,
∴∠C′EC=2×32°=64°,
∴∠AEC=180°﹣64°=116°=6960′,所以②错误;
∴∠BFD=∠EFD′﹣∠BFE=180°﹣2∠EFB=180°﹣64°=116°,所以④正确;
∵∠BGE=∠C′EC=2×32°=64°,所以③正确.
故答案为3.
三.解答题
15.解:∵∠B=∠BGD(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠BGC=∠F(已知),
∴CD∥EF(同位角相等,两直线平行).
∴AB∥EF(平行于同一直线的两直线平行).
∴∠B+∠F=180°(两直线平行,同旁内角互补).
故答案为:AB;内错角相等,两直线平行;EF;同位角相等,两直线平行;AB;EF;两直线平行,同旁内角互补.
16.解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴∠B=∠DEC(两直线平行,同位角相等).
又∵∠B=∠D(已知),
∴∠D=∠DEC(等量代换),
∴AD∥BC(内错角相等,两直线平行)、
故答案为:∠B,两直线平行,同位角相等,∠DEC,内错角相等,两直线平行.
17.解:∵CD平分∠ACB(已知),
∴∠1=∠2(角平分线的定义),
∵AC∥DE(已知),
∴∠1=∠3,
∴∠2=∠3(等量代换),
∵CD∥EF(已知),
∴∠4=∠3(两直线平行,内错角相等),∠2=∠5(两直线平行,同位角相等),
∴∠4=∠5(等量代换).
故答案为:角平分线的定义;3;两直线平行,内错角相等;两直线平行,同位角相等.
18.解:∵AB∥CD,
∴∠ABD=∠D=50°,∠ABC+∠C=180°.
∵BD平分∠ABC,
∴∠ABC=2∠ABD=100°.
∴∠C=180°﹣∠ABC
=180°﹣100°
=80°.
19.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
20.解:(1)成立,
理由:如图1中,作MN∥AB,则有MN∥CD,
∴∠1=∠BAM,∠2=∠DCM,
∴∠AMC=∠1+∠2=∠BAM+∠DCM.
(2)如图2,过点M作MH∥AB,
∵AB∥CD,∠NAD=64°,
∴∠NAD=∠ADC=64°,
∵DM平分∠ADC,∠ADC=64°,
∴∠MDC=∠ADC=32°,
∵BM平分∠ABC,∠ABC=44°,
∴∠ABM=∠ABC=22°,
∵AB∥CD,
∴AB∥CD∥MH,
∴∠ABM=∠BMH=22°,∠CDM=∠DMH=32°,
∴∠BMD=∠BMH+∠DMH=54°.
(3)如图3,过点M作MG∥AB,
∵BM平分∠ABC,DM平分∠ADC,∠ABC=β°,∠ADC=∠BAD=α°,
∴∠ABM=∠ABC=β°,∠CDM=∠ADC=α°,
∵AB∥CD,
∴AB∥CD∥MG,
∴∠BMG=180°﹣∠ABM=180°﹣β°,∠CDM=∠DMG=α°,
∴∠BMD=∠BMG+∠DMG=180°﹣β°+α°.
