人教版2022年八年级下册第16章《二次根式》章末测试卷 (word版,含详解)
文档属性
| 名称 | 人教版2022年八年级下册第16章《二次根式》章末测试卷 (word版,含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 304.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 08:48:21 | ||
图片预览



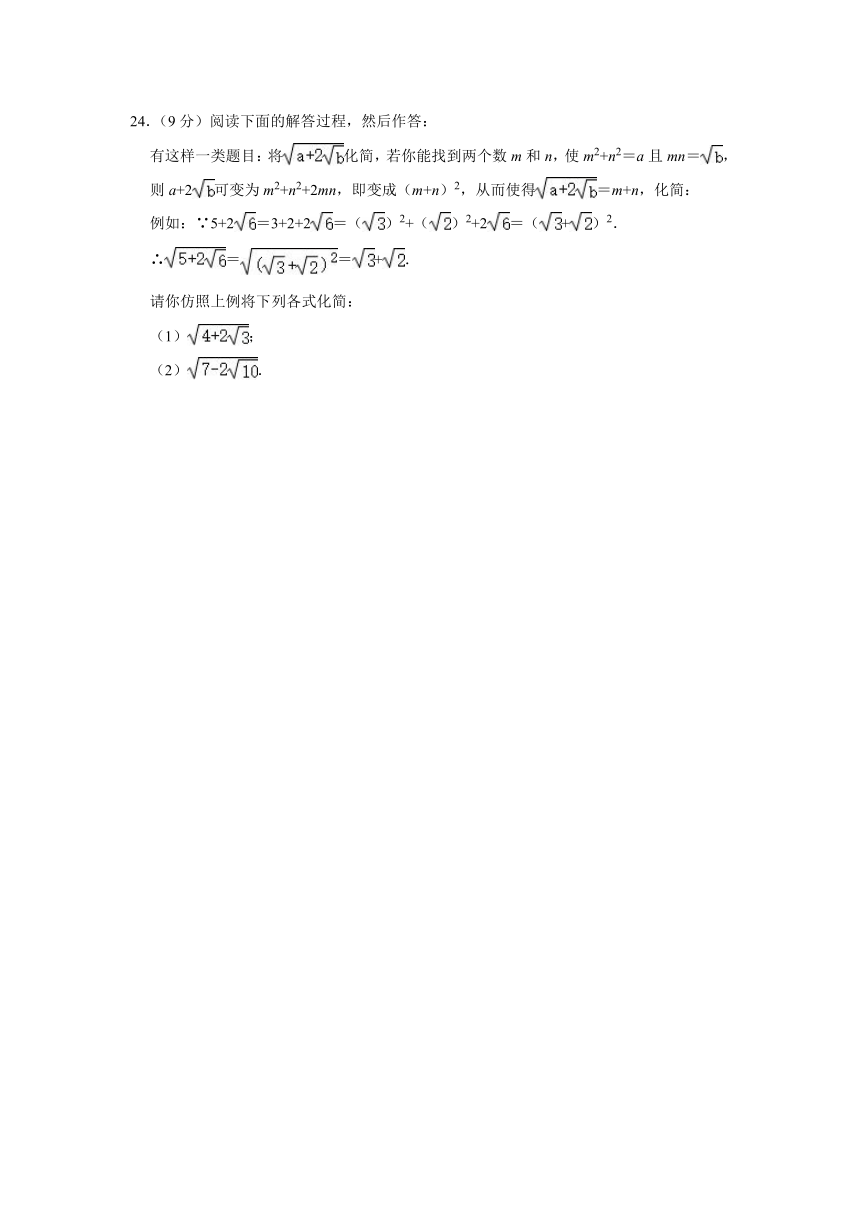
文档简介
人教版2022年八年级下册第16章《二次根式》章末测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.无论x取任何实数,下列一定是二次根式的是( )
A. B. C. D.
2.若式子有意义,则x的取值可以是( )
A.0 B.2 C.5 D.3
3.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
4.下列计算结果正确的是( )
A. B. C. D.
5.以下选项中,与的积为有理数的是( )
A. B.3 C.2 D.
6.若+=,则y的值为( )
A.8 B.15 C.3 D.2
7.已知三角形的三条边长为3,5,k,化简:=( )
A.8 B.﹣8 C.2k﹣10 D.10﹣2k
8.用※定义一种新运算:对于任意实数m和n,规定m※n=m2n﹣mn﹣3n,如:1※2=12×2﹣1×2﹣3×2=﹣6.则(﹣2)※结果为( )
A. B. C. D.
9.若a=1+,b=1﹣,则代数式的值为( )
A.3 B.±3 C.5 D.9
10.观察1:由完全平方公式可知,(﹣2)2=2﹣2×2×+22=9﹣4;
观察2:9+4=9+2×2=9+2×=2+2+2×=(+)2=(2+)2;
由此推出:,
请问:的结果是( )
A. B. C. D.
二.填空题(共8小题,满分24分,每小题3分)
11.计算:= .
12.如果y=+﹣2,那么xy的值是 .
13.把 a中根号外面的因式移到根号内的结果是 .
14.= .
15.如图所示,数轴上点A所表示的数是a,化简的结果为 .
16.(+)2021×(﹣)2022= .
17.已知x=+1,y=﹣1,则= .
18.如果一个三角形的三边长分别为a、b、c,记p=,那么这个三角形的面积S=,这就是著名的海伦﹣秦九韶公式.若一个三角形的三边长分别为4、5、6,则这个三角形的面积为 .
三.解答题(共6小题,满分46分)
19.(8分)计算:
(1);
(2).
20.(6分).
21.(8分)(1)先化简,再求值:,其中;
(2)当时,求的值.
22.(7分)已知二次根式.
(1)如果该二次根式=3,求a的值.
(2)已知为最简二次根式,且与能够合并,求a的值,并求出这两个次根式的积.
23.(8分)如图,有一张边长为6cm的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为cm.求:
(1)剪掉四个角后,制作长方体盒子的纸板的面积;
(2)长方体盒子的体积.
24.(9分)阅读下面的解答过程,然后作答:
有这样一类题目:将化简,若你能找到两个数m和n,使m2+n2=a且mn=,则a+2可变为m2+n2+2mn,即变成(m+n)2,从而使得=m+n,化简:
例如:∵5+2=3+2+2=()2+()2+2=(+)2.
∴==+.
请你仿照上例将下列各式化简:
(1);
(2).
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、,根号下部分有可能小于零,故此选项错误;
B、,根号下部分有可能小于零,故此选项错误;
C、,根号下部分不可能小于零,故此选项正确;
D、,根号下部分有可能小于零,故此选项错误.
选:C.
2.解:由题意可得,
解得:x≥3且x≠5,
A、0<3,故此选项不符合题意;
B、2<3,故此选项不符合题意;
C、x=5时,原式没有意义,故此选项不符合题意;
D、x取3时,原式==0,故此选项符合题意;
选:D.
3.解:A选项被开方数是小数,可以化成分数,有分母,不符合题意;
B选项的被开方数含分母,不符合题意;
C选项是最简二次根式,符合题意;
D选项的被开方数中有能开的尽方的因数4,不符合题意;
选:C.
4.解:A、3与4不是同类二次根式,不能合并计算,故此选项不符合题意;
B、原式=2﹣=,故此选项不符合题意;
C、原式=,故此选项不符合题意;
D、原式==3,故此选项符合题意;
选:D.
5.解:A、×=是无理数,故选项错误;
B、×3=3是无理数,故选项错误;
C、×2=6是有理数,故选项正确;
D、×=是无理数,故选项错误.
选:C.
6.解:因为+=,
所以=﹣=3﹣2=,
所以y=3.
选:C.
7.解:∵三角形的三条边长为3,5,k,
∴2<k<8,
∴原式=9﹣k+k﹣1=8,
选:A.
8.解:原式=(﹣2)2×﹣(﹣2)×﹣3
=4+2﹣3
=3,
选:A.
9.解:原式====3.
选:A.
10.解:9﹣6
=9﹣2×3×
=9﹣2××
=9﹣2××
=﹣2××+
=(﹣)2,
∴
=
=﹣,
选:C.
二.填空题(共8小题,满分24分,每小题3分)
11.解:原式=3﹣﹣5.
故答案为:3﹣﹣5.
12.解:由题意得:5﹣x≥0,x﹣5≥0,
则x=5,
∴y=﹣2,
∴xy=,
故答案为:.
13.解:原式=﹣=﹣,
故答案为:﹣
14.解:∵3﹣<0,
∴=|3﹣|=﹣3,
故答案为:﹣3.
15.解:由数轴知a<﹣1,
则a+1<0,
∴原式=|a+1|=﹣(a+1)=﹣a﹣1,
故答案为:﹣a﹣1.
16.解:原式=[(+)×(﹣)]2021×(﹣)
=(﹣1)2021×(﹣)
=﹣1×(﹣)
=﹣,
故答案为:﹣.
17.解:原式=+
=+
=+
=,
故答案为:.
18.解:把a=4,b=5,c=6代入p=,可得:p=,
把a=4,b=5,c=6,p=代入S==,
故答案为:.
三.解答题(共6小题,满分46分)
19.解:(1)原式=(4﹣6+3)
=4﹣+
=8﹣12+6
=﹣4+6;
(2)原式=﹣2+2
=﹣2+2
=4.
20.解:原式=﹣9×
=﹣6
=﹣3|a|.
21.解:(1)原式=[﹣]
=[﹣]
=
=,
当x=2+时,
原式==;
(2)∵a=,
∴a==2﹣<1,
原式=
=
=﹣
=﹣(2+)
=﹣2﹣.
22.解:(1)∵=3,
∴a+2=9,
∴a=7;
(2)∵=,为最简二次根式与能够合并,
∴a+2=10,
∴a=8,
∴×=5,
∴这两个次根式的积为5.
23.解:(1)制作长方体盒子的纸板的面积为:(6)2﹣4×()2
=108﹣12
=96(cm2);
(2)长方体盒子的体积:(6﹣2)(6﹣2)×
=4×4×
=48(cm3).
24.解:(1)∵4+2=1+3+2=12++2=(1+)2,
∴==1+;
(2)===﹣.
一.选择题(共10小题,满分30分,每小题3分)
1.无论x取任何实数,下列一定是二次根式的是( )
A. B. C. D.
2.若式子有意义,则x的取值可以是( )
A.0 B.2 C.5 D.3
3.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
4.下列计算结果正确的是( )
A. B. C. D.
5.以下选项中,与的积为有理数的是( )
A. B.3 C.2 D.
6.若+=,则y的值为( )
A.8 B.15 C.3 D.2
7.已知三角形的三条边长为3,5,k,化简:=( )
A.8 B.﹣8 C.2k﹣10 D.10﹣2k
8.用※定义一种新运算:对于任意实数m和n,规定m※n=m2n﹣mn﹣3n,如:1※2=12×2﹣1×2﹣3×2=﹣6.则(﹣2)※结果为( )
A. B. C. D.
9.若a=1+,b=1﹣,则代数式的值为( )
A.3 B.±3 C.5 D.9
10.观察1:由完全平方公式可知,(﹣2)2=2﹣2×2×+22=9﹣4;
观察2:9+4=9+2×2=9+2×=2+2+2×=(+)2=(2+)2;
由此推出:,
请问:的结果是( )
A. B. C. D.
二.填空题(共8小题,满分24分,每小题3分)
11.计算:= .
12.如果y=+﹣2,那么xy的值是 .
13.把 a中根号外面的因式移到根号内的结果是 .
14.= .
15.如图所示,数轴上点A所表示的数是a,化简的结果为 .
16.(+)2021×(﹣)2022= .
17.已知x=+1,y=﹣1,则= .
18.如果一个三角形的三边长分别为a、b、c,记p=,那么这个三角形的面积S=,这就是著名的海伦﹣秦九韶公式.若一个三角形的三边长分别为4、5、6,则这个三角形的面积为 .
三.解答题(共6小题,满分46分)
19.(8分)计算:
(1);
(2).
20.(6分).
21.(8分)(1)先化简,再求值:,其中;
(2)当时,求的值.
22.(7分)已知二次根式.
(1)如果该二次根式=3,求a的值.
(2)已知为最简二次根式,且与能够合并,求a的值,并求出这两个次根式的积.
23.(8分)如图,有一张边长为6cm的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为cm.求:
(1)剪掉四个角后,制作长方体盒子的纸板的面积;
(2)长方体盒子的体积.
24.(9分)阅读下面的解答过程,然后作答:
有这样一类题目:将化简,若你能找到两个数m和n,使m2+n2=a且mn=,则a+2可变为m2+n2+2mn,即变成(m+n)2,从而使得=m+n,化简:
例如:∵5+2=3+2+2=()2+()2+2=(+)2.
∴==+.
请你仿照上例将下列各式化简:
(1);
(2).
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、,根号下部分有可能小于零,故此选项错误;
B、,根号下部分有可能小于零,故此选项错误;
C、,根号下部分不可能小于零,故此选项正确;
D、,根号下部分有可能小于零,故此选项错误.
选:C.
2.解:由题意可得,
解得:x≥3且x≠5,
A、0<3,故此选项不符合题意;
B、2<3,故此选项不符合题意;
C、x=5时,原式没有意义,故此选项不符合题意;
D、x取3时,原式==0,故此选项符合题意;
选:D.
3.解:A选项被开方数是小数,可以化成分数,有分母,不符合题意;
B选项的被开方数含分母,不符合题意;
C选项是最简二次根式,符合题意;
D选项的被开方数中有能开的尽方的因数4,不符合题意;
选:C.
4.解:A、3与4不是同类二次根式,不能合并计算,故此选项不符合题意;
B、原式=2﹣=,故此选项不符合题意;
C、原式=,故此选项不符合题意;
D、原式==3,故此选项符合题意;
选:D.
5.解:A、×=是无理数,故选项错误;
B、×3=3是无理数,故选项错误;
C、×2=6是有理数,故选项正确;
D、×=是无理数,故选项错误.
选:C.
6.解:因为+=,
所以=﹣=3﹣2=,
所以y=3.
选:C.
7.解:∵三角形的三条边长为3,5,k,
∴2<k<8,
∴原式=9﹣k+k﹣1=8,
选:A.
8.解:原式=(﹣2)2×﹣(﹣2)×﹣3
=4+2﹣3
=3,
选:A.
9.解:原式====3.
选:A.
10.解:9﹣6
=9﹣2×3×
=9﹣2××
=9﹣2××
=﹣2××+
=(﹣)2,
∴
=
=﹣,
选:C.
二.填空题(共8小题,满分24分,每小题3分)
11.解:原式=3﹣﹣5.
故答案为:3﹣﹣5.
12.解:由题意得:5﹣x≥0,x﹣5≥0,
则x=5,
∴y=﹣2,
∴xy=,
故答案为:.
13.解:原式=﹣=﹣,
故答案为:﹣
14.解:∵3﹣<0,
∴=|3﹣|=﹣3,
故答案为:﹣3.
15.解:由数轴知a<﹣1,
则a+1<0,
∴原式=|a+1|=﹣(a+1)=﹣a﹣1,
故答案为:﹣a﹣1.
16.解:原式=[(+)×(﹣)]2021×(﹣)
=(﹣1)2021×(﹣)
=﹣1×(﹣)
=﹣,
故答案为:﹣.
17.解:原式=+
=+
=+
=,
故答案为:.
18.解:把a=4,b=5,c=6代入p=,可得:p=,
把a=4,b=5,c=6,p=代入S==,
故答案为:.
三.解答题(共6小题,满分46分)
19.解:(1)原式=(4﹣6+3)
=4﹣+
=8﹣12+6
=﹣4+6;
(2)原式=﹣2+2
=﹣2+2
=4.
20.解:原式=﹣9×
=﹣6
=﹣3|a|.
21.解:(1)原式=[﹣]
=[﹣]
=
=,
当x=2+时,
原式==;
(2)∵a=,
∴a==2﹣<1,
原式=
=
=﹣
=﹣(2+)
=﹣2﹣.
22.解:(1)∵=3,
∴a+2=9,
∴a=7;
(2)∵=,为最简二次根式与能够合并,
∴a+2=10,
∴a=8,
∴×=5,
∴这两个次根式的积为5.
23.解:(1)制作长方体盒子的纸板的面积为:(6)2﹣4×()2
=108﹣12
=96(cm2);
(2)长方体盒子的体积:(6﹣2)(6﹣2)×
=4×4×
=48(cm3).
24.解:(1)∵4+2=1+3+2=12++2=(1+)2,
∴==1+;
(2)===﹣.
