华东师大版八年级下册数学 19.1.2 矩形的判定 课件 (共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.1.2 矩形的判定 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 125.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
矩形的判定
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线平分且相等;
矩形的性质:
判定1
有一个角是直角的平行四边形
是矩形
A
B
C
D
∵平行四边形ABCD中, ∠B=90 °,
∴四边形ABCD是矩形.
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A= ∠B= ∠C=90°,
∴ ∠A + ∠B = 180°,
∠B + ∠C = 180°,
∴AD∥BC, AB∥DC,
∴四边形ABCD是平行四边形.
∵ ∠A=90°,
∴四边形ABCD是矩形.
特殊性质1
矩形的四个角是直角
判定2
三个角是直角是四边形是矩形
A
B
C
D
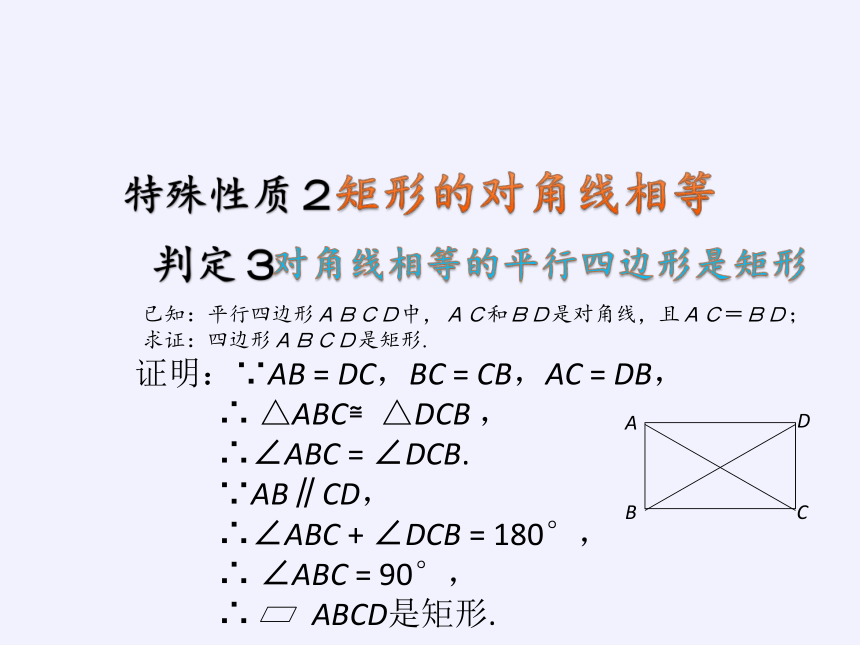
证明:∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ ABCD是矩形.
特殊性质2
矩形的对角线相等
判定3
对角线相等的平行四边形是矩形
已知:平行四边形ABCD中,AC和BD是对角线,且AC=BD;
求证:四边形ABCD是矩形.
6
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形 .
有三个角是直角的四边形是矩形 .
矩形的判定
例1、已知平行四边形ABCD的对角线AC、BD交于O,△AOB
是等边三角形,AB = 4cm,求这个平行四边形的面积.
A
B
C
D
O
S
ABCD
∴ =AB·BC = 4×4 =16
cm
2
解:∵ABCD是平行四边形,
∴AC = 2OA,BD = 2OB.
∵OA = OB,
∴AC =BD,
∴ ABCD是矩形.
在Rt△ABC中,
∵AB = 4cm,AC=2AO=8cm,
∴BC=
例2: 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.
已知:如图, ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
∴∠BGC=90°.同理可证∠AFB=∠AED=90°.
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形).
证明:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵BG平分∠ABC,CG平分∠BCD,
例3、如图,O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
A
B
C
D
O
E
F
G
H
证明: ∵四边形ABCD是平行四边形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分).
∵AE=BF =CG=DH,
∴OE=OF=OG=OH.
∴四边形EFGH是平行四边形(对角线互相平分的四边形是平行四边形).
∵EO+OG=OF+OH,
即EG=FH,
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形).
A
B
C
D
O
E
F
G
H
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形.
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
随堂练习
2.已知:矩形ABCD的两条对角线相交于点O,
∠AOD= 120°,AB=4cm,求矩形对角线的长.
解:∵四边形ABCD是矩形,∴AC=BD(矩形的对角
线相等).又 , ,
∴OA=OD.∴∠AOD=120°,∴ .
又∠DAB=90°(矩形的四个角都是直角),
∴BD=2AB=2×4cm=8cm.
3.在平行四边形ABCD中,对角线AC 、BD相交于G,EF过G,且AF⊥BC, 求证:四边形AFCE是矩形.
证明:∵四边形ABCD为平行四边形,∴GA=GC,AE∥FC,
∴∠EAG=∠FCG,在△AGE和△CGF中,∠EAG=∠FCG, AG=CG,
∠AGE=∠CGF,∴△AGE≌△CGF,∴AE=CF,∴四边形AECF为平
行四边形,又∵AF⊥BC,
∴∠AFC=90°,则四边形AECF为矩形.
谢 谢
矩形的判定
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线平分且相等;
矩形的性质:
判定1
有一个角是直角的平行四边形
是矩形
A
B
C
D
∵平行四边形ABCD中, ∠B=90 °,
∴四边形ABCD是矩形.
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A= ∠B= ∠C=90°,
∴ ∠A + ∠B = 180°,
∠B + ∠C = 180°,
∴AD∥BC, AB∥DC,
∴四边形ABCD是平行四边形.
∵ ∠A=90°,
∴四边形ABCD是矩形.
特殊性质1
矩形的四个角是直角
判定2
三个角是直角是四边形是矩形
A
B
C
D
证明:∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ ABCD是矩形.
特殊性质2
矩形的对角线相等
判定3
对角线相等的平行四边形是矩形
已知:平行四边形ABCD中,AC和BD是对角线,且AC=BD;
求证:四边形ABCD是矩形.
6
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形 .
有三个角是直角的四边形是矩形 .
矩形的判定
例1、已知平行四边形ABCD的对角线AC、BD交于O,△AOB
是等边三角形,AB = 4cm,求这个平行四边形的面积.
A
B
C
D
O
S
ABCD
∴ =AB·BC = 4×4 =16
cm
2
解:∵ABCD是平行四边形,
∴AC = 2OA,BD = 2OB.
∵OA = OB,
∴AC =BD,
∴ ABCD是矩形.
在Rt△ABC中,
∵AB = 4cm,AC=2AO=8cm,
∴BC=
例2: 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.
已知:如图, ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
∴∠BGC=90°.同理可证∠AFB=∠AED=90°.
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形).
证明:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵BG平分∠ABC,CG平分∠BCD,
例3、如图,O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
A
B
C
D
O
E
F
G
H
证明: ∵四边形ABCD是平行四边形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分).
∵AE=BF =CG=DH,
∴OE=OF=OG=OH.
∴四边形EFGH是平行四边形(对角线互相平分的四边形是平行四边形).
∵EO+OG=OF+OH,
即EG=FH,
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形).
A
B
C
D
O
E
F
G
H
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形.
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
随堂练习
2.已知:矩形ABCD的两条对角线相交于点O,
∠AOD= 120°,AB=4cm,求矩形对角线的长.
解:∵四边形ABCD是矩形,∴AC=BD(矩形的对角
线相等).又 , ,
∴OA=OD.∴∠AOD=120°,∴ .
又∠DAB=90°(矩形的四个角都是直角),
∴BD=2AB=2×4cm=8cm.
3.在平行四边形ABCD中,对角线AC 、BD相交于G,EF过G,且AF⊥BC, 求证:四边形AFCE是矩形.
证明:∵四边形ABCD为平行四边形,∴GA=GC,AE∥FC,
∴∠EAG=∠FCG,在△AGE和△CGF中,∠EAG=∠FCG, AG=CG,
∠AGE=∠CGF,∴△AGE≌△CGF,∴AE=CF,∴四边形AECF为平
行四边形,又∵AF⊥BC,
∴∠AFC=90°,则四边形AECF为矩形.
谢 谢
