安徽省合肥市庐阳区2021-2022学年九年级上学期期末(统考)数学试卷(word解析版)
文档属性
| 名称 | 安徽省合肥市庐阳区2021-2022学年九年级上学期期末(统考)数学试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 885.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 10:14:35 | ||
图片预览



文档简介
安徽合肥市庐阳区2021-2022学年九上期末(统考)数学试卷(原卷)
一、选择题(本大题共10小题,每小题4分,满分40分)
1、己知,那么下列等式中,不成立的是( )
A B C D 4x=3y
2、若反比例函数y=的图象经过点(1,-2),则k的值是( )
A -2 B 2 C D -
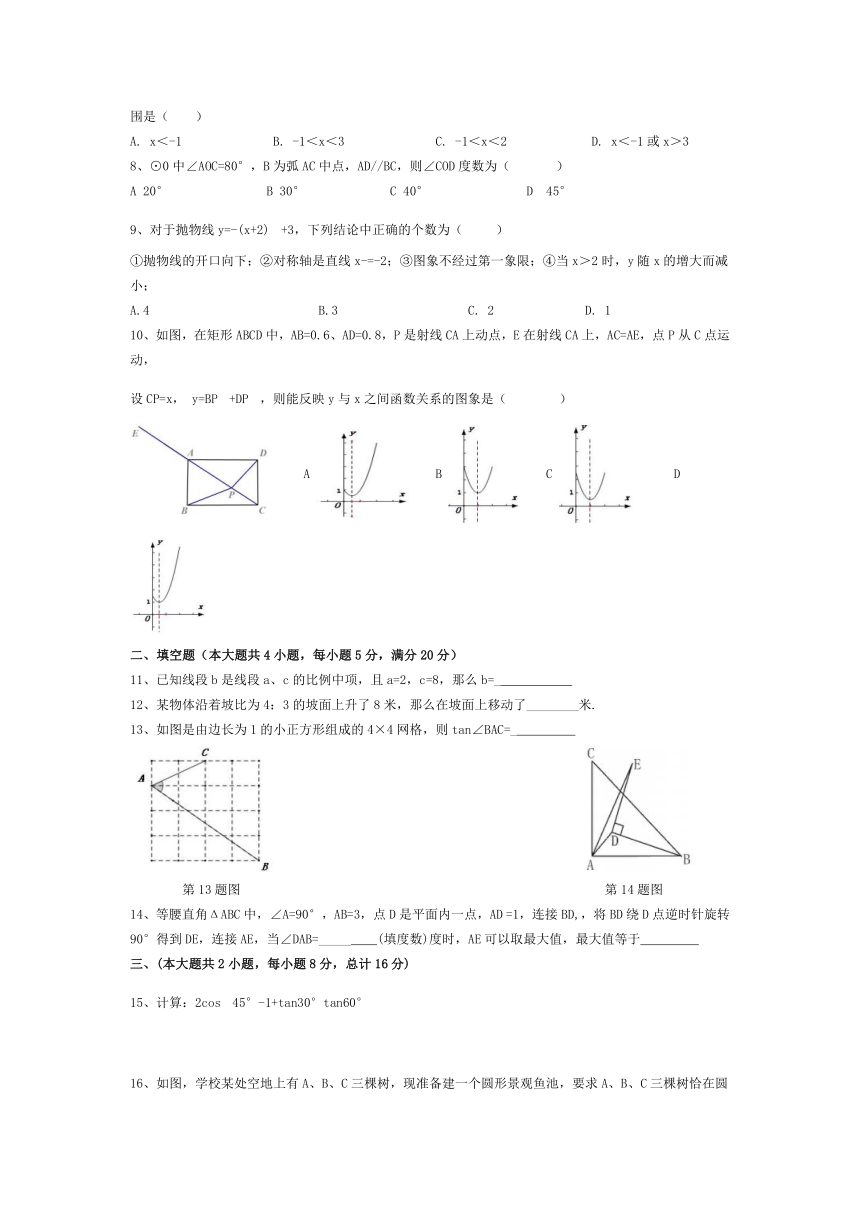
3、观察如图所示的正五角星,下列说法正确的是( )
A.既是轴对称图形,也是中心对称图形 B.不是轴对称图形,是中心对称图形
C.不是中心对称图形,是轴对称图形 D.既不是轴对称图形,也不是中心对称图形
第3题图 第5题图 第6题图 第8题图
4、已知,RtΔABC中,∠C= 90°,AC=6,AB=10,则cosB的值为( )
A B C D
5、如图,A、B、C分别是双曲线y1= (x<0)与y2= (x>0)及x轴上的点,AB//x轴,ΔABC的面积为2,则k的值是( )
A. -3 B. -2 C - D -
6、如图,ΔABC中,点D是边BC上一点,下列条件中,不能判定ΔABC与ΔABD相似的是( )
A. AB=BD BC B.∠BDA=∠BAC C. ∠ADC=∠C+∠B D. AD BC=AB AC
7、已知抛物线y=ax+bx+c(a>0)过(-1,0),且对称轴是直线x=1,则当y>0时,自变量x的取值范围是( )
A. x<-1 B. -1<x<3 C. -1<x<2 D. x<-1或x>3
8、⊙0中∠AOC=80°,B为弧AC中点,AD//BC,则∠COD度数为( )
A 20° B 30° C 40° D 45°
9、对于抛物线y=-(x+2)+3,下列结论中正确的个数为( )
①抛物线的开口向下;②对称轴是直线x-=-2;③图象不经过第一象限;④当x>2时,y随x的增大而减小;
A.4 B.3 C. 2 D. 1
10、如图,在矩形ABCD中,AB=0.6、AD=0.8,P是射线CA上动点,E在射线CA上,AC=AE,点P从C点运动,
设CP=x, y=BP+DP,则能反映y与x之间函数关系的图象是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知线段b是线段a、c的比例中项,且a=2,c=8,那么b=_
12、某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了________米.
13、如图是由边长为1的小正方形组成的4×4网格,则tan∠BAC=_
第13题图 第14题图
14、等腰直角ΔABC中,∠A=90°,AB=3,点D是平面内一点,AD =1,连接BD,,将BD绕D点逆时针旋转90°得到DE,连接AE,当∠DAB=_____ (填度数)度时,AE可以取最大值,最大值等于
三、(本大题共2小题,每小题8分,总计16分)
15、计算:2cos45°-1+tan30°tan60°
16、如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O
四、(本大题共2小题,每小题8分,总计16分)
17、(本小题8分)如图是一个6×6的正方形网格和平面直角坐标系,网格的每个小正方形边长为1,顶点都为格点的三角形我们称作格点三角形,如图ΔABC是格点三角形。
(1)将△ABC绕点A顺时针旋转90°,得到对应图形△AB1C1;
(2)在网格中,以B为位似中心,同侧将△BAC按2:1 放大,对应得到△BA2C2,画出△BA2C2,直接写出点C2坐标.
18、(本小题8分)如图,直线y1 =k1x+b与双曲线y2 =(x>0)在第一 象限内交于A、B两点,已知A(1,m)、
B(2,1) .
求直线和双曲线解析式;
(2)根据图象直接写出不等式y1<y2的解集.
五、(本大题共2小题,每小题10分,总计20分)
19、如图,数学兴趣小组为测量旗杆CD和教学楼AB的高,先在E处用高1.5米的测角仪EF测得教学楼顶端A的仰角∠AFH为45°,此时旗杆顶端D恰好在视线FA上,再向前走12米在G处(G在CD上),又测得教学楼顶端A的仰角∠AGH为60°,点B、C、E三点在同一水平线上。
(1)求旗杆CD的高
(2)求教学楼AB的高(结果用准确值表示) .
20、(本小题 10分)如图,线段AB是圆O的直径,O是圆心,C、D是圆上的点,且OD//BC。过点O作OE⊥BC于点E,交BD于点F。若AB=4,∠AOD=60°,求EF的长.
(本大题共1小题,每小题12分,总计12分)
21、(本小题12分)如图,A(-1,0),B(1,0),一抛物线顶点为(0,2),且过A、B两点,C、D是抛物线上且位于x轴上方的点,CD//x轴, CE⊥x轴于点E,DF⊥x轴于点F。
(1)求抛物线解析式;(2)若四边形EFDC是正方形,求的值.
七、(本大题共1小题,每小题12分,总计12分)
22、(本小题12分)某超市以10元/个的价格购进一批新型儿童玩具,当以17元个的价格出售时,每天可以售出50个。春节期间,在确保不亏本的前提下采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具.
设该玩具的售价降低了x元,每天的销售量为y个,直接写出y与x的函数关系式及自变量x的取值范围.
设销售这种玩具一天可获利润为w元,求w与x之间的函数关系式.
(3)这种玩具的售价定为每个多少元时,商店每天获得的利润最大?
(本大题共1小题,每小题14分,总计14分)
23、(本小题14分)ΔABC中,∠ACB=90°,AC=BC=1,点E为BC边上一点,点D为AC延长线上一点,CE=CD,连接BD、AE,并延长AE交BD于F,设CE=x.
(1)求证:△ACE∽△BFE;
(2)若F恰好是BD中点,求x的值;
(3)设y=,当x=时,求y的值.
安徽合肥市庐阳区2021-2022学年九上期末(统考)数学试卷(解析版)
温馨提示:本试卷内容沪科版九上全册第21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、己知,那么下列等式中,不成立的是( )
A B C D 4x=3y
【答案】B
【解析】设x=3k,y=4k; A ,本选项成立; B ,本选项不成立;
C ,本选项成立; D ∵,∴4x=3y,本选项成立;
故选B
2、若反比例函数y=的图象经过点(1,-2),则k的值是( )
A -2 B 2 C D -
【答案】A
【解析】∵若反比例函数y=的图象经过点(1,-2),则k=1×(-2)=-2,
故选A
3、观察如图所示的正五角星,下列说法正确的是( )
A.既是轴对称图形,也是中心对称图形 B.不是轴对称图形,是中心对称图形
C.不是中心对称图形,是轴对称图形 D.既不是轴对称图形,也不是中心对称图形
【答案】C
【解析】正五角星不是中心对称图形,是轴对称图形
故选C
4、已知,RtΔABC中,∠C= 90°,AC=6,AB=10,则cosB的值为( )
A B C D
【答案】B
【解析】在RtΔABC中,BC=,cosB=
故选B
5、如图,A、B、C分别是双曲线y1= (x<0)与y2= (x>0)及x轴上的点,AB//x轴,ΔABC的面积为2,则k的值是( )
A. -3 B. -2 C - D -
【答案】A
【解析】连接OA、OB,则SΔOAB=SΔABC=2,由题意得:1-k=2SΔOAB=4,∴k=-3
故选A
6、如图,ΔABC中,点D是边BC上一点,下列条件中,不能判定ΔABC与ΔABD相似的是( )
A. AB=BD BC B.∠BDA=∠BAC C. ∠ADC=∠C+∠B D. AD BC=AB AC
【答案】D
【解析】A ∵AB=BD BC,AB:BD=BC:AB,∠B=∠B,∴ΔABC∽ΔDBA,条件能判定;
B ∵∠BDA=∠BAC,∠B=∠B,∴ΔABC∽ΔDBA,条件能判定;
C. ∵∠ADC=∠C+∠B,C. ∠ADC=∠BAD+∠B,∴∠BDA=∠BAC,∵∠B=∠B,∴ΔABC∽ΔDBA,条件能判定;
D ∵AD BC=AB AC,∴BC:AB=AC:AD,∵∠B≠∠DAC,∴条件不能判定ΔABC与ΔABD相似;
故选D
7、已知抛物线y=ax+bx+c(a>0)过(-1,0),且对称轴是直线x=1,则当y>0时,自变量x的取值范围是( )
A. x<-1 B. -1<x<3 C. -1<x<2 D. x<-1或x>3
【答案】D
【解析】∴抛物线y=ax+bx+c(a>0)过(-1,0),且对称轴是直线x=1,则抛物线y=ax+bx+c(a>0)x轴的两个交点分别为(-1,0)、(3,0);且抛物线y=ax+bx+c(a>0)开口向上,
∴当y>0时,自变量x的取值范围是x<-1或x>3
故选D
8、⊙0中∠AOC=80°,B为弧AC中点,AD//BC,则∠COD度数为( )
A 20° B 30° C 40° D 45°
【答案】C
【解析】∵∠AOC=80°,OA=OC,∴∠OCA=50°,连接OB,∵B为弧AC中点,∴∠BOC=40°,∵OB=OC,∴∠OCB=70°,
∴∠ACB=70°-50°=20°,∵AD//BC,∴∠DAC=∠ACB=20°,∴∠COD=2∠DAC=40°,
故选C
9、对于抛物线y=-(x+2)+3,下列结论中正确的个数为( )
①抛物线的开口向下;②对称轴是直线x-=-2;③图象不经过第一象限;④当x>2时,y随x的增大而减小;
A.4 B.3 C. 2 D. 1
【答案】A
【解析】①∵a=-1<0,∴抛物线的开口向下,正确; ②对称轴是直线x-=-2,正确;
③∵y=-(x+2)+3=-x-4x-1,图像与y轴交点坐标为(0,-1),在y轴的下方,∴图像不经过第一象限,正确;
④图像开口向下,当x>-2时,抛物线下降的,∴当x>2时,y随x的增大而减小,正确;
故选A
10、如图,在矩形ABCD中,AB=0.6、AD=0.8,P是射线CA上动点,E在射线CA上,AC=AE,点P从C点运动,设CP=x, y=BP+DP,则能反映y与x之间函数关系的图象是( )
A B C D
【答案】A
【解析】如图,以BC、CD所在的直线分别为x、y轴,C为原点,建立如图所示的平面角坐标系,则A(-0.8,0.6)、
B(-0.8,0)、D(0,0.6)、C(0,0);∵PC=x,则P(-0.8x,0.6x)
∴BP=(0.8-0.8x)+(0.6x)=x-1.28x+0.64;
PD=(-0.8x)+(0.6-0.6x)=x-0.72x+0.36;
∴y=BP+DP=2x-2x+1=2(x-)+(x≥0);该函数图像开口向上,对称轴为直线x=,当x=0时,y=1
故选A
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知线段b是线段a、c的比例中项,且a=2,c=8,那么b=_
【答案】4
【解析】∵线段b是线段a、c的比例中项,∴b=ac=2×8=16,b=4
故答案:4
12、某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了________米.
【答案】10
【解析】由题意可知: i=,Δh=8米,则Δl=6米;坡面上移动了=(米)
故答案:10
13、如图是由边长为1的小正方形组成的4×4网格,则tan∠BAC=_
【答案】2
【解析】连接BC、由勾股定理得:AC=2+1=5,AB=3+4=25,BC=2+4=20,即AC+BC=AB,∴ΔABC为RtΔ,
∵AC=,BC=2,∴tan∠BAC=
故答案:2
14、等腰直角ΔABC中,∠A=90°,AB=3,点D是平面内一点,AD =1,连接BD,将BD绕D点逆时针旋转90°得到DE,连接AE,当∠DAB=_____ 度(填度数),AE可以取最大值,最大值等于
【答案】135°,3+
【解析】如图1,连接BE、CE,∵∠BDE=90°,BD=DE,∴ΔBDE为等腰直角三角形;∴,
∵∠ABD+∠CBD=∠EBC+∠CBD=45°,∴∠ABD=∠CBD,∴ΔABD∽ΔCBE,∴∠ECB=∠DAB,
在ΔACE中,AC=3为定值,当∠ACE度数最大时,AE最大,当A、C、E三点共线时,AE最大,如图2;
此时,∠ECB=135°,∴∠DAB=135°;
∵ΔABD∽ΔCBE,∴,∵AD=1,∴EC=,∴AE=3+;
三、(本大题共2小题,每小题8分,总计16分)
15、计算:2cos45°-1+tan30°tan60°
【答案】1
【分析】利用特殊角的三角函数值求解
【解析】原式=2×()-1+×=1-1+1=1
16、如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,
请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O
【答案】见解析
【分析】连接AB、BC,分别作线段AB、BC的垂直平分线交于点O,再以点O为圆心,OA长为半径作圆.
【解析】如图所示:⊙O为作的圆
四、(本大题共2小题,每小题8分,总计16分)
17、(本小题8分)如图是一个6×6的正方形网格和平面直角坐标系,网格的每个小正方形边长为1,顶点都为格点的三角形我们称作格点三角形,如图ΔABC是格点三角形。
(1)将△ABC绕点A顺时针旋转90°,得到对应图形△AB1C1;
(2)在网格中,以B为位似中心,同侧将△BAC按2:1 放大,对应得到△BA2C2,画出△BA2C2,直接写出点C2坐标.
【答案】(1)见解析;(2)见解析;
【分析】(1)根据旋转画出对应图形△AB1C1;
(2)根据图形的位似,画出△BA2C2,写出点C2坐标为( 4,0)
【解析】(1)如图所示;(2)如图所示,( 4,0)
18、(本小题8分)如图,直线y1=k1x+b与双曲线y2 =(x>0)在第一象限内交于A、B两点,已知A(1,m)、
B(2,1)
(1)求直线和双曲线解析式;
(2)根据图象直接写出不等式y1<y2的解集.
【答案】(1);y1=-x+3; (2)
【分析】(1)待定系数法求出直线和双曲线解析式;
(2)由图像直接观察可求解;
【解析】(1)∵点A(1,m)、B(2,1)在上,∴k=2×1=2,即,由1×m=2,求出m=2,A(1,2)
由题意得:,解得,∴y1=-x+3;
(2)根据图像观察当y1<y2时x的取值范围是:,∴不等式y1<y2的解集为
五、(本大题共2小题,每小题10分,总计20分)
19、如图,数学兴趣小组为测量旗杆CD和教学楼AB的高,先在E处用高1.5米的测角仪EF测得教学楼顶端A的仰角∠AFH为45°,此时旗杆顶端D恰好在视线FA上,再向前走12米在G处(G在CD上),又测得教学楼顶端A的仰角∠AGH为60°,点B、C、E三点在同一水平线上。
(1)求旗杆CD的高
(2)求教学楼AB的高(结果用准确值表示) .
【答案】(1)13.5米;(2)19.5+6(米)
【分析】(1)利用等腰直角三角形的性质求出DG长即可;
(2)利用利用等腰直角三角形的性质确定AH=HF=HG+12,再利用三角函数确定AH=HG,求出HG,再求AH;
【解析】(1)在RtΔDGF中,∠DFG=45°,∴DG=DF=12米,CD=DG+CG=DG+EF=12+1.5=13.5(米)
(2)由题意,,,
,,∴,∴, ,∴HG=6(+1)
,∵HB=CG=EF=1.5米,.
20、(本小题10分)如图,线段AB是圆O的直径,O是圆心,C、D是圆上的点,且OD//BC,过点O作OE⊥BC于点E,交BD于点F。若AB=4,∠AOD=60°,求EF的长.
【答案】
【分析】两直线平行同位角相等及OE⊥BC得ΔBOE为含30°角的直角三角形,求出BE、OF长;再证ΔDOF∽ΔBEF,
得出EF=OF;
【解析】∵OD//BC,∠AOD=60°,∴∠ABC=60°,∵AB=4,∴OB=OD=2,∴OE⊥BC,∴在RtΔBOE中,∠BOE=30°,
∴BE=1,OC=;
∵OD//BC,∴ΔDOF∽ΔBEF,∴OF:EF=OD:BE=2,即OF=2EF,∴EF=
(本大题共1小题,每小题12分,总计12分)
21、(本小题12分)如图,A(-1,0),B(1,0),一抛物线顶点为(0,2),且过A、B两点,C、D是抛物线上且位于
x轴上方的点,CD//x轴, CE⊥x轴于点E,DF⊥x轴于点F。
(1)求抛物线解析式;(2)若四边形EFDC是正方形,求的值.
【答案】(1)y=-2x+2;(2)
【分析】(1)待定系数法求出抛物线解析式;
(2)AB=2,设点的坐标为(x,-2x+2),利用等式求出x,即可求出CD
【解析】(1)设抛物线为y=ax+2,将(1,0)代入,得:a+2=0,∵a=-2,∴y=-2x+2;
(2)设点的坐标为(x,-2x+2),四边形EFDC是正方形,则-2x+2=2x,即x+x-1=0,
解出x1=,x2=(舍去),∴CD=-1,∵AB=2,∴=.
七、(本大题共1小题,每小题12分,总计12分)
22、(本小题12分)某超市以10元/个的价格购进一批新型儿童玩具,当以17元个的价格出售时,每天可以售出50个。春节期间,在确保不亏本的前提下采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具.
设该玩具的售价降低了x元,每天的销售量为y个,直接写出y与x的函数关系式及自变量x的取值范围.
设销售这种玩具一天可获利润为w元,求w与x之间的函数关系式.
(3)这种玩具的售价定为每个多少元时,商店每天获得的利润最大?
【答案】(1)y=50+10x(0≤x≤7)
【分析】(1)由题意可出y与x的函数关系式及自变量x的取值范围
(2)由题意可出w与x之间的函数关系式.
(3)配方,根据二次函数的性质,可求每天获得的最大利润;
【解析】(1)由题意得,y=50+×5=50+10x,∴y与x的函数关系式为:y=50+10x,
自变量取值范围是y=50+10x;
(2)由题意得,;
(3)配方为,因为,所以当时,此时售价为16元/个,
每天的销售量为60个,.
(本大题共1小题,每小题14分,总计14分)
23、(本小题14分)ΔABC中,∠ACB=90°,AC=BC=1,点E为BC边上一点,点D为AC延长线上一点,CE=CD,连接BD、AE,并延长AE交BD于F,设CE=x.
(1)求证:△ACE∽△BFE;
(2)若F恰好是BD中点,求x的值;
(3)设y=,当x=时,求y的值.
【答案】(1)见解析; (2)-1; (3)
【分析】(1)先证明ΔACE≌ΔBCD,利用三角形相似判定一证△ACE∽△BFE;
(2)利用线段垂直平分线的性质;
(3)勾股定理求出AE,从而得出BE,长度;△ACE∽△BFE,求出BF;
【解析】(1)∵AC=BC,CE=CD,∠ACE=∠BCD=90°,∴ΔACE≌ΔBCD,∴∠CAE=∠CBD,∵∠AEC=∠BEF,
∴△ACE∽△BFE;
(2)∵△ACE∽△BFE,∴∠BFE=∠ACE=90°,∴AF⊥BD,又F恰好是BD中点,∴AF为线段BD的垂直平分线,
∴AD=AB=,∴CD=-1;∵ CE=CD,∴x=-1;
(3)∵CE=x,∴BE=1-x,AE=,∵ΔACE≌ΔBCD,∴BD=AE=,
∵△ACE∽△BFE,∴AE:BE=AC:BF,则BF=,∴
当x=,y=
一、选择题(本大题共10小题,每小题4分,满分40分)
1、己知,那么下列等式中,不成立的是( )
A B C D 4x=3y
2、若反比例函数y=的图象经过点(1,-2),则k的值是( )
A -2 B 2 C D -
3、观察如图所示的正五角星,下列说法正确的是( )
A.既是轴对称图形,也是中心对称图形 B.不是轴对称图形,是中心对称图形
C.不是中心对称图形,是轴对称图形 D.既不是轴对称图形,也不是中心对称图形
第3题图 第5题图 第6题图 第8题图
4、已知,RtΔABC中,∠C= 90°,AC=6,AB=10,则cosB的值为( )
A B C D
5、如图,A、B、C分别是双曲线y1= (x<0)与y2= (x>0)及x轴上的点,AB//x轴,ΔABC的面积为2,则k的值是( )
A. -3 B. -2 C - D -
6、如图,ΔABC中,点D是边BC上一点,下列条件中,不能判定ΔABC与ΔABD相似的是( )
A. AB=BD BC B.∠BDA=∠BAC C. ∠ADC=∠C+∠B D. AD BC=AB AC
7、已知抛物线y=ax+bx+c(a>0)过(-1,0),且对称轴是直线x=1,则当y>0时,自变量x的取值范围是( )
A. x<-1 B. -1<x<3 C. -1<x<2 D. x<-1或x>3
8、⊙0中∠AOC=80°,B为弧AC中点,AD//BC,则∠COD度数为( )
A 20° B 30° C 40° D 45°
9、对于抛物线y=-(x+2)+3,下列结论中正确的个数为( )
①抛物线的开口向下;②对称轴是直线x-=-2;③图象不经过第一象限;④当x>2时,y随x的增大而减小;
A.4 B.3 C. 2 D. 1
10、如图,在矩形ABCD中,AB=0.6、AD=0.8,P是射线CA上动点,E在射线CA上,AC=AE,点P从C点运动,
设CP=x, y=BP+DP,则能反映y与x之间函数关系的图象是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知线段b是线段a、c的比例中项,且a=2,c=8,那么b=_
12、某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了________米.
13、如图是由边长为1的小正方形组成的4×4网格,则tan∠BAC=_
第13题图 第14题图
14、等腰直角ΔABC中,∠A=90°,AB=3,点D是平面内一点,AD =1,连接BD,,将BD绕D点逆时针旋转90°得到DE,连接AE,当∠DAB=_____ (填度数)度时,AE可以取最大值,最大值等于
三、(本大题共2小题,每小题8分,总计16分)
15、计算:2cos45°-1+tan30°tan60°
16、如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O
四、(本大题共2小题,每小题8分,总计16分)
17、(本小题8分)如图是一个6×6的正方形网格和平面直角坐标系,网格的每个小正方形边长为1,顶点都为格点的三角形我们称作格点三角形,如图ΔABC是格点三角形。
(1)将△ABC绕点A顺时针旋转90°,得到对应图形△AB1C1;
(2)在网格中,以B为位似中心,同侧将△BAC按2:1 放大,对应得到△BA2C2,画出△BA2C2,直接写出点C2坐标.
18、(本小题8分)如图,直线y1 =k1x+b与双曲线y2 =(x>0)在第一 象限内交于A、B两点,已知A(1,m)、
B(2,1) .
求直线和双曲线解析式;
(2)根据图象直接写出不等式y1<y2的解集.
五、(本大题共2小题,每小题10分,总计20分)
19、如图,数学兴趣小组为测量旗杆CD和教学楼AB的高,先在E处用高1.5米的测角仪EF测得教学楼顶端A的仰角∠AFH为45°,此时旗杆顶端D恰好在视线FA上,再向前走12米在G处(G在CD上),又测得教学楼顶端A的仰角∠AGH为60°,点B、C、E三点在同一水平线上。
(1)求旗杆CD的高
(2)求教学楼AB的高(结果用准确值表示) .
20、(本小题 10分)如图,线段AB是圆O的直径,O是圆心,C、D是圆上的点,且OD//BC。过点O作OE⊥BC于点E,交BD于点F。若AB=4,∠AOD=60°,求EF的长.
(本大题共1小题,每小题12分,总计12分)
21、(本小题12分)如图,A(-1,0),B(1,0),一抛物线顶点为(0,2),且过A、B两点,C、D是抛物线上且位于x轴上方的点,CD//x轴, CE⊥x轴于点E,DF⊥x轴于点F。
(1)求抛物线解析式;(2)若四边形EFDC是正方形,求的值.
七、(本大题共1小题,每小题12分,总计12分)
22、(本小题12分)某超市以10元/个的价格购进一批新型儿童玩具,当以17元个的价格出售时,每天可以售出50个。春节期间,在确保不亏本的前提下采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具.
设该玩具的售价降低了x元,每天的销售量为y个,直接写出y与x的函数关系式及自变量x的取值范围.
设销售这种玩具一天可获利润为w元,求w与x之间的函数关系式.
(3)这种玩具的售价定为每个多少元时,商店每天获得的利润最大?
(本大题共1小题,每小题14分,总计14分)
23、(本小题14分)ΔABC中,∠ACB=90°,AC=BC=1,点E为BC边上一点,点D为AC延长线上一点,CE=CD,连接BD、AE,并延长AE交BD于F,设CE=x.
(1)求证:△ACE∽△BFE;
(2)若F恰好是BD中点,求x的值;
(3)设y=,当x=时,求y的值.
安徽合肥市庐阳区2021-2022学年九上期末(统考)数学试卷(解析版)
温馨提示:本试卷内容沪科版九上全册第21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、己知,那么下列等式中,不成立的是( )
A B C D 4x=3y
【答案】B
【解析】设x=3k,y=4k; A ,本选项成立; B ,本选项不成立;
C ,本选项成立; D ∵,∴4x=3y,本选项成立;
故选B
2、若反比例函数y=的图象经过点(1,-2),则k的值是( )
A -2 B 2 C D -
【答案】A
【解析】∵若反比例函数y=的图象经过点(1,-2),则k=1×(-2)=-2,
故选A
3、观察如图所示的正五角星,下列说法正确的是( )
A.既是轴对称图形,也是中心对称图形 B.不是轴对称图形,是中心对称图形
C.不是中心对称图形,是轴对称图形 D.既不是轴对称图形,也不是中心对称图形
【答案】C
【解析】正五角星不是中心对称图形,是轴对称图形
故选C
4、已知,RtΔABC中,∠C= 90°,AC=6,AB=10,则cosB的值为( )
A B C D
【答案】B
【解析】在RtΔABC中,BC=,cosB=
故选B
5、如图,A、B、C分别是双曲线y1= (x<0)与y2= (x>0)及x轴上的点,AB//x轴,ΔABC的面积为2,则k的值是( )
A. -3 B. -2 C - D -
【答案】A
【解析】连接OA、OB,则SΔOAB=SΔABC=2,由题意得:1-k=2SΔOAB=4,∴k=-3
故选A
6、如图,ΔABC中,点D是边BC上一点,下列条件中,不能判定ΔABC与ΔABD相似的是( )
A. AB=BD BC B.∠BDA=∠BAC C. ∠ADC=∠C+∠B D. AD BC=AB AC
【答案】D
【解析】A ∵AB=BD BC,AB:BD=BC:AB,∠B=∠B,∴ΔABC∽ΔDBA,条件能判定;
B ∵∠BDA=∠BAC,∠B=∠B,∴ΔABC∽ΔDBA,条件能判定;
C. ∵∠ADC=∠C+∠B,C. ∠ADC=∠BAD+∠B,∴∠BDA=∠BAC,∵∠B=∠B,∴ΔABC∽ΔDBA,条件能判定;
D ∵AD BC=AB AC,∴BC:AB=AC:AD,∵∠B≠∠DAC,∴条件不能判定ΔABC与ΔABD相似;
故选D
7、已知抛物线y=ax+bx+c(a>0)过(-1,0),且对称轴是直线x=1,则当y>0时,自变量x的取值范围是( )
A. x<-1 B. -1<x<3 C. -1<x<2 D. x<-1或x>3
【答案】D
【解析】∴抛物线y=ax+bx+c(a>0)过(-1,0),且对称轴是直线x=1,则抛物线y=ax+bx+c(a>0)x轴的两个交点分别为(-1,0)、(3,0);且抛物线y=ax+bx+c(a>0)开口向上,
∴当y>0时,自变量x的取值范围是x<-1或x>3
故选D
8、⊙0中∠AOC=80°,B为弧AC中点,AD//BC,则∠COD度数为( )
A 20° B 30° C 40° D 45°
【答案】C
【解析】∵∠AOC=80°,OA=OC,∴∠OCA=50°,连接OB,∵B为弧AC中点,∴∠BOC=40°,∵OB=OC,∴∠OCB=70°,
∴∠ACB=70°-50°=20°,∵AD//BC,∴∠DAC=∠ACB=20°,∴∠COD=2∠DAC=40°,
故选C
9、对于抛物线y=-(x+2)+3,下列结论中正确的个数为( )
①抛物线的开口向下;②对称轴是直线x-=-2;③图象不经过第一象限;④当x>2时,y随x的增大而减小;
A.4 B.3 C. 2 D. 1
【答案】A
【解析】①∵a=-1<0,∴抛物线的开口向下,正确; ②对称轴是直线x-=-2,正确;
③∵y=-(x+2)+3=-x-4x-1,图像与y轴交点坐标为(0,-1),在y轴的下方,∴图像不经过第一象限,正确;
④图像开口向下,当x>-2时,抛物线下降的,∴当x>2时,y随x的增大而减小,正确;
故选A
10、如图,在矩形ABCD中,AB=0.6、AD=0.8,P是射线CA上动点,E在射线CA上,AC=AE,点P从C点运动,设CP=x, y=BP+DP,则能反映y与x之间函数关系的图象是( )
A B C D
【答案】A
【解析】如图,以BC、CD所在的直线分别为x、y轴,C为原点,建立如图所示的平面角坐标系,则A(-0.8,0.6)、
B(-0.8,0)、D(0,0.6)、C(0,0);∵PC=x,则P(-0.8x,0.6x)
∴BP=(0.8-0.8x)+(0.6x)=x-1.28x+0.64;
PD=(-0.8x)+(0.6-0.6x)=x-0.72x+0.36;
∴y=BP+DP=2x-2x+1=2(x-)+(x≥0);该函数图像开口向上,对称轴为直线x=,当x=0时,y=1
故选A
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知线段b是线段a、c的比例中项,且a=2,c=8,那么b=_
【答案】4
【解析】∵线段b是线段a、c的比例中项,∴b=ac=2×8=16,b=4
故答案:4
12、某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了________米.
【答案】10
【解析】由题意可知: i=,Δh=8米,则Δl=6米;坡面上移动了=(米)
故答案:10
13、如图是由边长为1的小正方形组成的4×4网格,则tan∠BAC=_
【答案】2
【解析】连接BC、由勾股定理得:AC=2+1=5,AB=3+4=25,BC=2+4=20,即AC+BC=AB,∴ΔABC为RtΔ,
∵AC=,BC=2,∴tan∠BAC=
故答案:2
14、等腰直角ΔABC中,∠A=90°,AB=3,点D是平面内一点,AD =1,连接BD,将BD绕D点逆时针旋转90°得到DE,连接AE,当∠DAB=_____ 度(填度数),AE可以取最大值,最大值等于
【答案】135°,3+
【解析】如图1,连接BE、CE,∵∠BDE=90°,BD=DE,∴ΔBDE为等腰直角三角形;∴,
∵∠ABD+∠CBD=∠EBC+∠CBD=45°,∴∠ABD=∠CBD,∴ΔABD∽ΔCBE,∴∠ECB=∠DAB,
在ΔACE中,AC=3为定值,当∠ACE度数最大时,AE最大,当A、C、E三点共线时,AE最大,如图2;
此时,∠ECB=135°,∴∠DAB=135°;
∵ΔABD∽ΔCBE,∴,∵AD=1,∴EC=,∴AE=3+;
三、(本大题共2小题,每小题8分,总计16分)
15、计算:2cos45°-1+tan30°tan60°
【答案】1
【分析】利用特殊角的三角函数值求解
【解析】原式=2×()-1+×=1-1+1=1
16、如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,
请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O
【答案】见解析
【分析】连接AB、BC,分别作线段AB、BC的垂直平分线交于点O,再以点O为圆心,OA长为半径作圆.
【解析】如图所示:⊙O为作的圆
四、(本大题共2小题,每小题8分,总计16分)
17、(本小题8分)如图是一个6×6的正方形网格和平面直角坐标系,网格的每个小正方形边长为1,顶点都为格点的三角形我们称作格点三角形,如图ΔABC是格点三角形。
(1)将△ABC绕点A顺时针旋转90°,得到对应图形△AB1C1;
(2)在网格中,以B为位似中心,同侧将△BAC按2:1 放大,对应得到△BA2C2,画出△BA2C2,直接写出点C2坐标.
【答案】(1)见解析;(2)见解析;
【分析】(1)根据旋转画出对应图形△AB1C1;
(2)根据图形的位似,画出△BA2C2,写出点C2坐标为( 4,0)
【解析】(1)如图所示;(2)如图所示,( 4,0)
18、(本小题8分)如图,直线y1=k1x+b与双曲线y2 =(x>0)在第一象限内交于A、B两点,已知A(1,m)、
B(2,1)
(1)求直线和双曲线解析式;
(2)根据图象直接写出不等式y1<y2的解集.
【答案】(1);y1=-x+3; (2)
【分析】(1)待定系数法求出直线和双曲线解析式;
(2)由图像直接观察可求解;
【解析】(1)∵点A(1,m)、B(2,1)在上,∴k=2×1=2,即,由1×m=2,求出m=2,A(1,2)
由题意得:,解得,∴y1=-x+3;
(2)根据图像观察当y1<y2时x的取值范围是:,∴不等式y1<y2的解集为
五、(本大题共2小题,每小题10分,总计20分)
19、如图,数学兴趣小组为测量旗杆CD和教学楼AB的高,先在E处用高1.5米的测角仪EF测得教学楼顶端A的仰角∠AFH为45°,此时旗杆顶端D恰好在视线FA上,再向前走12米在G处(G在CD上),又测得教学楼顶端A的仰角∠AGH为60°,点B、C、E三点在同一水平线上。
(1)求旗杆CD的高
(2)求教学楼AB的高(结果用准确值表示) .
【答案】(1)13.5米;(2)19.5+6(米)
【分析】(1)利用等腰直角三角形的性质求出DG长即可;
(2)利用利用等腰直角三角形的性质确定AH=HF=HG+12,再利用三角函数确定AH=HG,求出HG,再求AH;
【解析】(1)在RtΔDGF中,∠DFG=45°,∴DG=DF=12米,CD=DG+CG=DG+EF=12+1.5=13.5(米)
(2)由题意,,,
,,∴,∴, ,∴HG=6(+1)
,∵HB=CG=EF=1.5米,.
20、(本小题10分)如图,线段AB是圆O的直径,O是圆心,C、D是圆上的点,且OD//BC,过点O作OE⊥BC于点E,交BD于点F。若AB=4,∠AOD=60°,求EF的长.
【答案】
【分析】两直线平行同位角相等及OE⊥BC得ΔBOE为含30°角的直角三角形,求出BE、OF长;再证ΔDOF∽ΔBEF,
得出EF=OF;
【解析】∵OD//BC,∠AOD=60°,∴∠ABC=60°,∵AB=4,∴OB=OD=2,∴OE⊥BC,∴在RtΔBOE中,∠BOE=30°,
∴BE=1,OC=;
∵OD//BC,∴ΔDOF∽ΔBEF,∴OF:EF=OD:BE=2,即OF=2EF,∴EF=
(本大题共1小题,每小题12分,总计12分)
21、(本小题12分)如图,A(-1,0),B(1,0),一抛物线顶点为(0,2),且过A、B两点,C、D是抛物线上且位于
x轴上方的点,CD//x轴, CE⊥x轴于点E,DF⊥x轴于点F。
(1)求抛物线解析式;(2)若四边形EFDC是正方形,求的值.
【答案】(1)y=-2x+2;(2)
【分析】(1)待定系数法求出抛物线解析式;
(2)AB=2,设点的坐标为(x,-2x+2),利用等式求出x,即可求出CD
【解析】(1)设抛物线为y=ax+2,将(1,0)代入,得:a+2=0,∵a=-2,∴y=-2x+2;
(2)设点的坐标为(x,-2x+2),四边形EFDC是正方形,则-2x+2=2x,即x+x-1=0,
解出x1=,x2=(舍去),∴CD=-1,∵AB=2,∴=.
七、(本大题共1小题,每小题12分,总计12分)
22、(本小题12分)某超市以10元/个的价格购进一批新型儿童玩具,当以17元个的价格出售时,每天可以售出50个。春节期间,在确保不亏本的前提下采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具.
设该玩具的售价降低了x元,每天的销售量为y个,直接写出y与x的函数关系式及自变量x的取值范围.
设销售这种玩具一天可获利润为w元,求w与x之间的函数关系式.
(3)这种玩具的售价定为每个多少元时,商店每天获得的利润最大?
【答案】(1)y=50+10x(0≤x≤7)
【分析】(1)由题意可出y与x的函数关系式及自变量x的取值范围
(2)由题意可出w与x之间的函数关系式.
(3)配方,根据二次函数的性质,可求每天获得的最大利润;
【解析】(1)由题意得,y=50+×5=50+10x,∴y与x的函数关系式为:y=50+10x,
自变量取值范围是y=50+10x;
(2)由题意得,;
(3)配方为,因为,所以当时,此时售价为16元/个,
每天的销售量为60个,.
(本大题共1小题,每小题14分,总计14分)
23、(本小题14分)ΔABC中,∠ACB=90°,AC=BC=1,点E为BC边上一点,点D为AC延长线上一点,CE=CD,连接BD、AE,并延长AE交BD于F,设CE=x.
(1)求证:△ACE∽△BFE;
(2)若F恰好是BD中点,求x的值;
(3)设y=,当x=时,求y的值.
【答案】(1)见解析; (2)-1; (3)
【分析】(1)先证明ΔACE≌ΔBCD,利用三角形相似判定一证△ACE∽△BFE;
(2)利用线段垂直平分线的性质;
(3)勾股定理求出AE,从而得出BE,长度;△ACE∽△BFE,求出BF;
【解析】(1)∵AC=BC,CE=CD,∠ACE=∠BCD=90°,∴ΔACE≌ΔBCD,∴∠CAE=∠CBD,∵∠AEC=∠BEF,
∴△ACE∽△BFE;
(2)∵△ACE∽△BFE,∴∠BFE=∠ACE=90°,∴AF⊥BD,又F恰好是BD中点,∴AF为线段BD的垂直平分线,
∴AD=AB=,∴CD=-1;∵ CE=CD,∴x=-1;
(3)∵CE=x,∴BE=1-x,AE=,∵ΔACE≌ΔBCD,∴BD=AE=,
∵△ACE∽△BFE,∴AE:BE=AC:BF,则BF=,∴
当x=,y=
同课章节目录
