2.3.2平行线的性质(2) 课件(共25张PPT)
文档属性
| 名称 | 2.3.2平行线的性质(2) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 853.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 12:33:02 | ||
图片预览






文档简介
(共25张PPT)
2.3.2平行线的性质(2)
第二章
相交线与平行线
2021-2022学年七年级数学下册(北师大版)
学习目标
1.复习巩固平行线的判定和性质,能应用判定和性质进行简单的推理或计算。
2.进一步学会识图,能将复杂图形分解为基本图形,会对已知条件和求证结论进行转化。
导入新课
平行线的判定与平行线的性质:
平行线的判定 平行线的性质
同位角相等,两直线平行. 两直线平行,同位角相等.
内错角相等,两直线平行. 两直线平行,内错角相等.
同旁内角互补,两直线平行. 两直线平行,同旁内角互补.
讲授新课
平行线性质与判定的综合运用
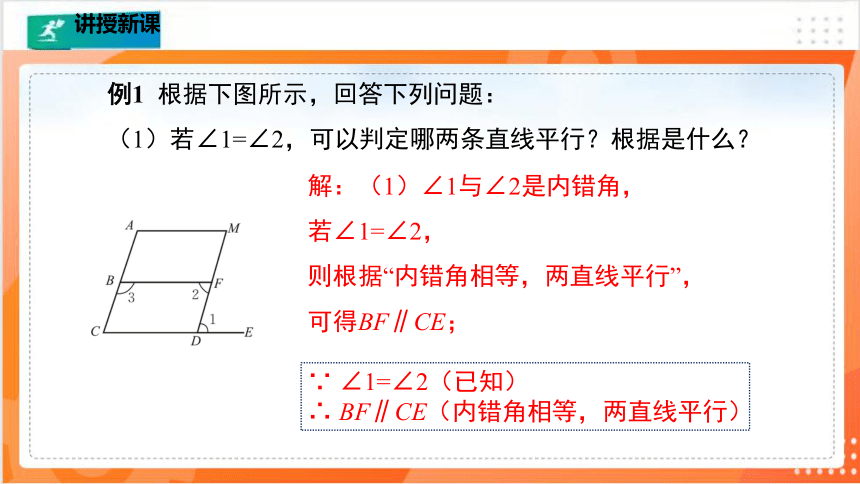
例1 根据下图所示,回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
讲授新课
例1 根据下图所示,回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
解:(1)∠1与∠2是内错角,
若∠1=∠2,
则根据“内错角相等,两直线平行”,可得BF∥CE;
∵ ∠1=∠2(已知)
∴ BF∥CE(内错角相等,两直线平行)
讲授新课
例1 根据下图所示,回答下列问题:
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
解:(1)∠2与∠M是同位角,
若∠2=∠M,
则根据“同位角相等,两直线平行”,可得AM∥BF;
∵ ∠2=∠M(已知)
∴ AM∥BF(同位角相等,两直线平行)
讲授新课
例1 根据下图所示,回答下列问题:
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
解:(1)∠2与∠3是同旁内角,
若∠2+∠3=180°,
则根据“同旁内角互补,两直线平行”,可得AC∥MD;
∵ ∠2+∠3=180°(已知)
∴ AC∥MD(同旁内角互补,两直线平行).
讲授新课
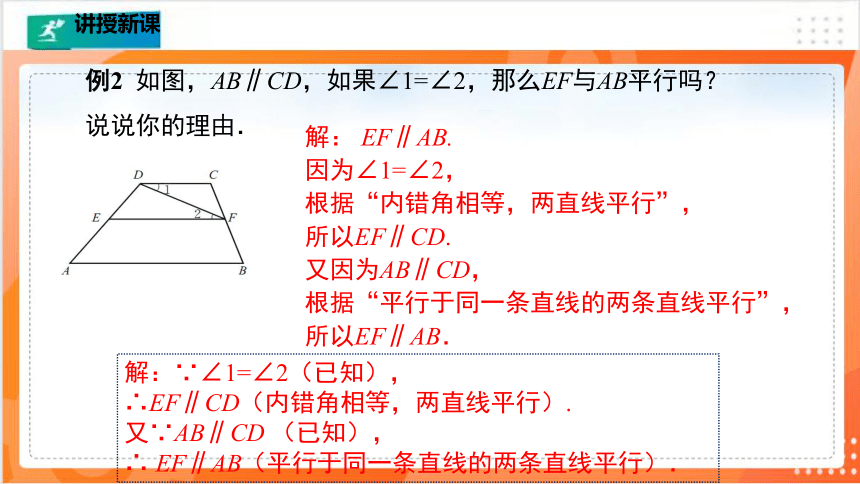
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由.
解: EF∥AB.
因为∠1=∠2,
根据“内错角相等,两直线平行”,
所以EF∥CD.
又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以EF∥AB.
解:∵∠1=∠2(已知),
∴EF∥CD(内错角相等,两直线平行).
又∵AB∥CD (已知),
∴ EF∥AB(平行于同一条直线的两条直线平行).
讲授新课
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3的度数.
解:因为a∥b,
根据“两直线平行,内错角相等”.
所以∠2=∠1=107°.
因为c∥d,
根据“两直线平行,同旁内角互补”,
所以∠1+∠3=180°,
所以∠3= 180°-∠1=180°-107°=73°.
讲授新课
如图,AB//CD,试解决下列问题:
(1)如图1 , ∠1+∠2=______;
(2)如图2 , ∠1+∠2+∠3=_____;
A
B
C
D
1
2
B
A
E
C
D
1
2
3
图1
图2
180°
360°
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF+∠3=180°(两直线平行,同旁内角互补).
∵ EF∥AB (已知),
∴∠AEF+∠1=180°(两直线平行,同旁内角互补)
∵ ∠CEF+∠AEF=∠2
∴ ∠1+∠2+∠3= 360°.
F
“铅笔模型”
讲授新课
如图,AB//CD,试解决下列问题:
(1)如图1 , ∠1+∠2=______;
(2)如图2 , ∠1+∠2+∠3=_____;
(3)如图3 , ∠1+∠2+∠3+∠4= ;
(4)如图4 ,试探究∠1+∠2+∠3+∠4+…∠n= ;
A
B
C
D
1
2
B
A
E
C
D
1
2
3
图1
图2
180°
360°
B
A
E
C
D
F
1
2
4
3
B
A
E
C
D
N
1
2
n
图3
图4
540°
180°(n-1)
从特殊到一般
讲授新课
如图,如果AB ∥CD,请探索∠A 、∠C、∠E的关系,并说明理由.
∠E = ∠A +∠C
A
B
C
D
E
“猪脚模型”
F
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF=∠C(两直线平行,内错角相等).
∵ EF∥AB (已知),
∴∠AEF= ∠A (两直线平行,内错角相等)
∵ ∠AEC=∠CEF+∠AEF
∴ ∠AEC= ∠A + ∠C.
讲授新课
如图,若AB∥CD, 则:
A
B
C
D
E
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E.
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D.
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时: ∠A+∠ F1 +∠C
= ∠ E1 +∠ E2.
从特殊到一般
讲授新课
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
∠A+∠F1 + ∠ F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+∠Em-1+ ∠D.
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角,你能找到规律吗?
从特殊到一般
当堂检测
1.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β-∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
B
当堂检测
2.如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B.85°
C.95°
D.100°
B
当堂检测
3.如图,∠A=∠D,如果∠B=20°,那么∠C为( )
A.40° B.20°
C.60° D.70°
解:∵∠A=∠D(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠B=20°(已知),
∴∠C=∠B=20°(两直线平行,内错角相等).
B
当堂检测
4.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,
则∠4的度数是( )
A.35° B.70° C.90° D.110°
D
解:∵∠1=∠2 (已知),
∴a∥b(同位角相等,两直线平行),
∴∠3=∠5 (两直线平行,同位角相等).
∵∠3=70° (已知),
∴∠5=70° (等量代换),
∴∠4=180°-70°=110°(邻补角互补).
当堂检测
5.如图所示,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数.
解:因为AD∥EF,所以∠2=∠DAC.
因为∠1=∠2,所以∠1=∠DAC.
所以GD∥AC.
因为∠BAC=80°,∠B=∠C,
所以2∠C=180°-∠BAC=100°.
所以∠C=50°.
所以∠BDG=50°.
所以∠BDG=∠C.
当堂检测
如图,已知∠ABC与∠ECB互补,∠1=∠2,则∠P与∠Q一定相等吗?说说你的理由.
如果∠P和∠Q相等,那么PB∥CQ,
所以要判断∠P与∠Q是否相等,
只需判断PB和CQ是否平行.
要说明PB∥CQ,可以通过说明
∠PBC=∠BCQ来实现,由于∠1
=∠2,只需说明∠ABC=∠BCD
即可.
解析:
当堂检测
一定.
理由如下:因为∠ABC与∠ECB互补(已知),
所以AB∥ED(同旁内角互补,两直线平行).
所以∠ABC=∠BCD(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠PBC=∠BCQ.
所以PB∥CQ(内错角相等,两直线平行).
所以∠P=∠Q(两直线平行,内错角相等).
解:
当堂检测
6.著名的比萨斜塔建成于12世纪,从建成之日起就一直在倾斜.目前,它与地面所成的较小的角为85°(如图所示),它与地面所成的较大的角是多少度?你的依据是什么?
1
2
a
b
解:∵a∥b(已知),
∴∠1=85°(两直线平行,同位角相等).
∵ ∠1+ ∠2=180° (已知),
∴∠2=180° - ∠1=95°.
课堂小结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
https://www.21cnjy.com/help/help_extract.php
2.3.2平行线的性质(2)
第二章
相交线与平行线
2021-2022学年七年级数学下册(北师大版)
学习目标
1.复习巩固平行线的判定和性质,能应用判定和性质进行简单的推理或计算。
2.进一步学会识图,能将复杂图形分解为基本图形,会对已知条件和求证结论进行转化。
导入新课
平行线的判定与平行线的性质:
平行线的判定 平行线的性质
同位角相等,两直线平行. 两直线平行,同位角相等.
内错角相等,两直线平行. 两直线平行,内错角相等.
同旁内角互补,两直线平行. 两直线平行,同旁内角互补.
讲授新课
平行线性质与判定的综合运用
例1 根据下图所示,回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
讲授新课
例1 根据下图所示,回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
解:(1)∠1与∠2是内错角,
若∠1=∠2,
则根据“内错角相等,两直线平行”,可得BF∥CE;
∵ ∠1=∠2(已知)
∴ BF∥CE(内错角相等,两直线平行)
讲授新课
例1 根据下图所示,回答下列问题:
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
解:(1)∠2与∠M是同位角,
若∠2=∠M,
则根据“同位角相等,两直线平行”,可得AM∥BF;
∵ ∠2=∠M(已知)
∴ AM∥BF(同位角相等,两直线平行)
讲授新课
例1 根据下图所示,回答下列问题:
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
解:(1)∠2与∠3是同旁内角,
若∠2+∠3=180°,
则根据“同旁内角互补,两直线平行”,可得AC∥MD;
∵ ∠2+∠3=180°(已知)
∴ AC∥MD(同旁内角互补,两直线平行).
讲授新课
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由.
解: EF∥AB.
因为∠1=∠2,
根据“内错角相等,两直线平行”,
所以EF∥CD.
又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以EF∥AB.
解:∵∠1=∠2(已知),
∴EF∥CD(内错角相等,两直线平行).
又∵AB∥CD (已知),
∴ EF∥AB(平行于同一条直线的两条直线平行).
讲授新课
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3的度数.
解:因为a∥b,
根据“两直线平行,内错角相等”.
所以∠2=∠1=107°.
因为c∥d,
根据“两直线平行,同旁内角互补”,
所以∠1+∠3=180°,
所以∠3= 180°-∠1=180°-107°=73°.
讲授新课
如图,AB//CD,试解决下列问题:
(1)如图1 , ∠1+∠2=______;
(2)如图2 , ∠1+∠2+∠3=_____;
A
B
C
D
1
2
B
A
E
C
D
1
2
3
图1
图2
180°
360°
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF+∠3=180°(两直线平行,同旁内角互补).
∵ EF∥AB (已知),
∴∠AEF+∠1=180°(两直线平行,同旁内角互补)
∵ ∠CEF+∠AEF=∠2
∴ ∠1+∠2+∠3= 360°.
F
“铅笔模型”
讲授新课
如图,AB//CD,试解决下列问题:
(1)如图1 , ∠1+∠2=______;
(2)如图2 , ∠1+∠2+∠3=_____;
(3)如图3 , ∠1+∠2+∠3+∠4= ;
(4)如图4 ,试探究∠1+∠2+∠3+∠4+…∠n= ;
A
B
C
D
1
2
B
A
E
C
D
1
2
3
图1
图2
180°
360°
B
A
E
C
D
F
1
2
4
3
B
A
E
C
D
N
1
2
n
图3
图4
540°
180°(n-1)
从特殊到一般
讲授新课
如图,如果AB ∥CD,请探索∠A 、∠C、∠E的关系,并说明理由.
∠E = ∠A +∠C
A
B
C
D
E
“猪脚模型”
F
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF=∠C(两直线平行,内错角相等).
∵ EF∥AB (已知),
∴∠AEF= ∠A (两直线平行,内错角相等)
∵ ∠AEC=∠CEF+∠AEF
∴ ∠AEC= ∠A + ∠C.
讲授新课
如图,若AB∥CD, 则:
A
B
C
D
E
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E.
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D.
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时: ∠A+∠ F1 +∠C
= ∠ E1 +∠ E2.
从特殊到一般
讲授新课
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
∠A+∠F1 + ∠ F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+∠Em-1+ ∠D.
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角,你能找到规律吗?
从特殊到一般
当堂检测
1.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β-∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
B
当堂检测
2.如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B.85°
C.95°
D.100°
B
当堂检测
3.如图,∠A=∠D,如果∠B=20°,那么∠C为( )
A.40° B.20°
C.60° D.70°
解:∵∠A=∠D(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠B=20°(已知),
∴∠C=∠B=20°(两直线平行,内错角相等).
B
当堂检测
4.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,
则∠4的度数是( )
A.35° B.70° C.90° D.110°
D
解:∵∠1=∠2 (已知),
∴a∥b(同位角相等,两直线平行),
∴∠3=∠5 (两直线平行,同位角相等).
∵∠3=70° (已知),
∴∠5=70° (等量代换),
∴∠4=180°-70°=110°(邻补角互补).
当堂检测
5.如图所示,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数.
解:因为AD∥EF,所以∠2=∠DAC.
因为∠1=∠2,所以∠1=∠DAC.
所以GD∥AC.
因为∠BAC=80°,∠B=∠C,
所以2∠C=180°-∠BAC=100°.
所以∠C=50°.
所以∠BDG=50°.
所以∠BDG=∠C.
当堂检测
如图,已知∠ABC与∠ECB互补,∠1=∠2,则∠P与∠Q一定相等吗?说说你的理由.
如果∠P和∠Q相等,那么PB∥CQ,
所以要判断∠P与∠Q是否相等,
只需判断PB和CQ是否平行.
要说明PB∥CQ,可以通过说明
∠PBC=∠BCQ来实现,由于∠1
=∠2,只需说明∠ABC=∠BCD
即可.
解析:
当堂检测
一定.
理由如下:因为∠ABC与∠ECB互补(已知),
所以AB∥ED(同旁内角互补,两直线平行).
所以∠ABC=∠BCD(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠PBC=∠BCQ.
所以PB∥CQ(内错角相等,两直线平行).
所以∠P=∠Q(两直线平行,内错角相等).
解:
当堂检测
6.著名的比萨斜塔建成于12世纪,从建成之日起就一直在倾斜.目前,它与地面所成的较小的角为85°(如图所示),它与地面所成的较大的角是多少度?你的依据是什么?
1
2
a
b
解:∵a∥b(已知),
∴∠1=85°(两直线平行,同位角相等).
∵ ∠1+ ∠2=180° (已知),
∴∠2=180° - ∠1=95°.
课堂小结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
