莆田24中2021-2022学年人教A版(2019)数学高一下学期开学摸底考试试卷二卷(Word含答案解析)
文档属性
| 名称 | 莆田24中2021-2022学年人教A版(2019)数学高一下学期开学摸底考试试卷二卷(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 09:29:32 | ||
图片预览




文档简介
莆田24中2021-2022学年人教A版(2019)数学
高一下学期
开学摸底考试试卷二卷
【考试用时:120分钟】【满分:150分】
考试范围:人教A版(2019)必修第一册(占比80%)+人教A版(2019)必修第二册第六章(占比20%)
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作答无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知命题,,则命题p的否定为( )
A.,
B.,
C.,
D.,
2.若集合,或,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若,则( )
A.无最大值,有最小值8 B.无最大值,有最小值-4
C.有最大值8,有最小值-4 D.有最大值-4,无最小值
4.在中,内角A,B,C的对边分别为a,b,c,若,则的外接圆的面积为( )
A. B. C. D.
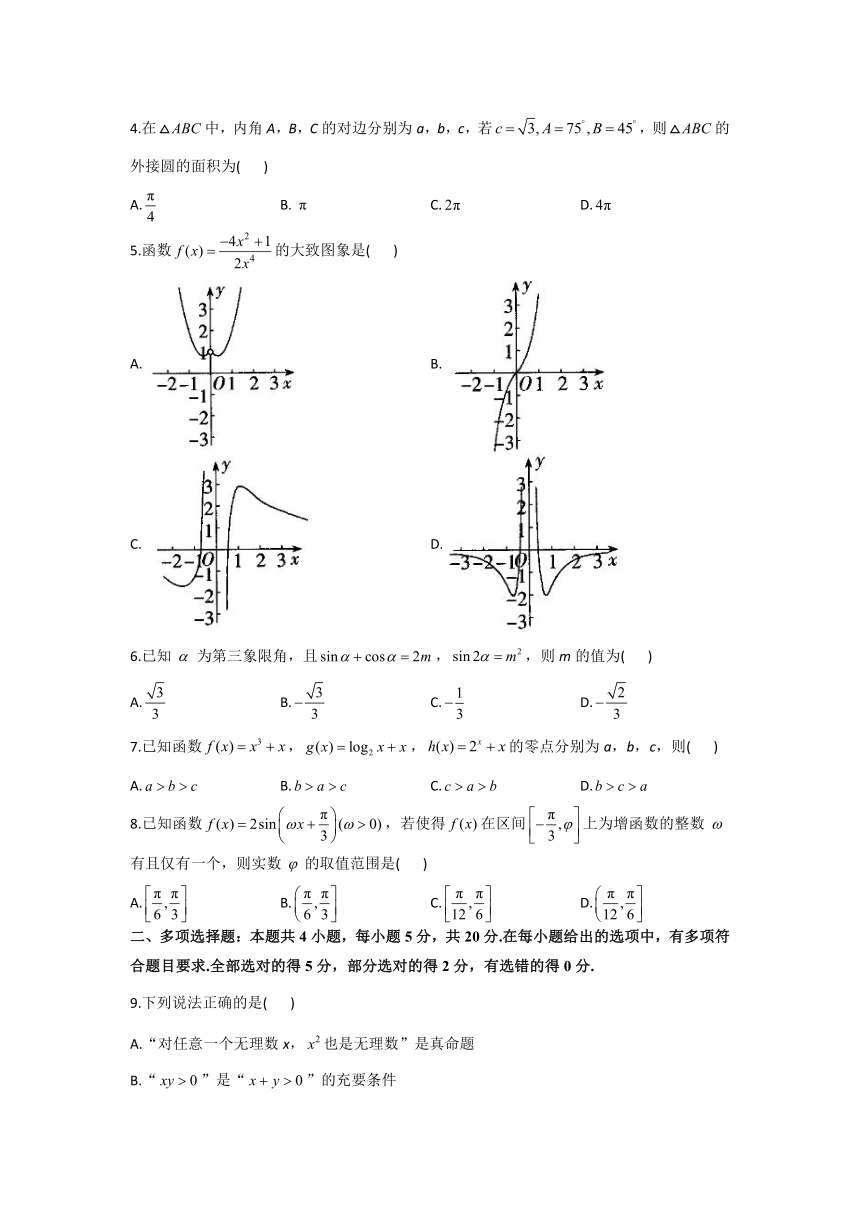
5.函数的大致图象是( )
A. B.
C. D.
6.已知为第三象限角,且,,则m的值为( )
A. B. C. D.
7.已知函数,,的零点分别为a,b,c,则( )
A. B. C. D.
8.已知函数,若使得在区间上为增函数的整数有且仅有一个,则实数的取值范围是( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列说法正确的是( )
A.“对任意一个无理数x,也是无理数”是真命题
B.“”是“”的充要条件
C.命题“,”的否定是“,”
D.若“”的一个必要不充分条件是“”,则实数m的取值范围是
10.设函数,对于任意的,,下列式子成立的是( )
A. B.
C. D.
11.已知向量在同一平面内且两两不共线,则下列命题为真命题的是( )
A.给定向量,总存在向量,使
B.给定向量,总存在实数和,使
C.给定向量,单位向量,正实数,总存在单位向量和实数,使
D.若,且存在单位向量和正实数,使,则
12.已知函数的图象关于点中心对称,且与直线的两个相邻交点间的距离为,则下列叙述正确的是( )
A.函数的最小正周期为
B.函数图象的对称中心为
C.函数的图象可由的图象向左平移个单位长度得到
D.函数的单调递增区间为
三、填空题:本题共4小题,每小题5分,共20分.
13.已知,且,则__________,____________.
14.如图,在中,M为边BC上不同于B,C的任意一点,点N满足.若,则的最小值为___________.
15.若对任意,恒成立,则a的取值范围为____________.
16.已知函数若方程有4个不同的实数根,,,,则的取值范围是____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知集合,或.
(1)当时,求;
(2)若“”是“”的充分不必要条件,且,求实数a的取值范围.
18.(12分)《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(1)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(2)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则市政府至少需要补贴多少元才能使该企业不亏损?
19. (12分)在中,角A,B,C的对边分别为a,b,c.已知.
(1)求的值;
(2)在边BC上取一点D,使得,求的值.
20. (12分)某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快,开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积y(单位:平方米)与经过月份的关系有两个函数模型与可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的覆盖面积是当初投放时的1000倍?(参考数据:,,,)
21. (12分)已知函数.
(1)求函数的周期;
(2)求函数在上的单调区间;
(3)若对任意,不等式恒成立,试求m的取值范围.
22. (12分)已知函数.
(1)当时,设,证明:函数在R上单调递增;
(2)若,恒成立,求实数a的取值范围;
(3)若函数在上有两个零点,求实数a的取值范围.
答案以及解析
1.答案:C
解析:在中,量词“”改为“”,结论“”改为“”,故选C.
2.答案:A
解析:或,
,
,但.
故“”是“”的充分不必要条件.
3.答案:D
解析:若,则,,当且仅当,即时等号成立,,有最大值-4,没有最小值.故选D.
4.答案:B
解析:在中,,所以.设的外接圆的半径为R,则由正弦定理,可得,解得,故的外接圆的面积,故选B.
5.答案:D
解析:易知函数是偶函数,排除选项B,C;当时,,对应点在第四象限,故排除A.故选D.
6.答案:B
解析:依题意得,
又,.
由是第三象限角知,,
,故选B.
7.答案:B
解析:函数的零点为函数与的图象交点的横坐标,函数的零点为函数与的图象交点的横坐标,
函数的零点为函数与的图象交点的横坐标,
在同一直角坐标系内作出函数,,与的图象如图所示:
由图可知:,,,,故选B.
8.答案:D
解析:因为在区间上为增函数,
所以,
可得.
当时,满足条件的整数可为1或2,不满足题意,舍去.
当时,由,知,所以,
所以有,即,
要使整数有且仅有一个,需,
解得.
综上,实数的取值范围为,故选D.
9.答案:CD
解析:是无理数,是有理数,故A错;
,时,,但,不是充要条件,故B错;
命题“,”的否定是“,”,故C正确;
若“”的一个必要不充分条件是“”,则且两个等号不同时取得,解得,故D正确.故选CD.
10.答案:ACD
解析:,,所以A成立;,,所以B不成立;易知函数在R上是单调递增函数,则,所以C成立;说明函数图象是下凹的,而函数图象是下凹的,所以D成立.故选ACD.
11.答案:ABD
解析:给定向量,显然存在向量,使,即,所以A是真命题.由平面向量的基本定理可得B是真命题.C选项中,取,设,则,即,解得,因为为单位向量,所以,所以C不是真命题.D选项中,,且向量的模都为1,又两两不共线,所以由三角形的三边关系可得,即.又,所以D是真命题.故选ABD.
12.答案:ACD
解析:对于A,根据与直线的两个相邻交点间的距离可知最小正周期,所以A正确;对于B,,又为图象的一个对称中心,所以,得,因为,所以,,令,得,所以函数图象的对称中心为,B错误;对于C,,则的图象可由函数的图象向左平移个单位长度得到,C正确;对于D,令,得,D正确.
13.答案:;
解析:由得,
所以,
所以
.
14.答案:
解析:根据题意,得.
因为三点共线,所以有,即,,所以,所以当时,取得最小值,为.
15.答案:
解析:,,根据题意知.
,
.
,(当且仅当时取等号),
,.
16.答案:
解析:作出函数的图象如图所示.
由方程有4个解,知,且.
由得.
由,关于直线对称,得,
.
,,,
.
因此的取值范围是.
17.答案:(1) 或.
(2).
解析:(1)当时,,
又或,
或.
(2)或,
.
由“”是“”的充分不必要条件,
得,
又,,
.
的取值范围是.
18.解析:(1)由题意可知,
每吨产品的平均加工处理成本为,
当且仅当,即(吨)时,才能使每吨产品的平均加工处理成本最低.
(2)设该企业每周获利为s元,则,
,当时,.
故该企业每周不能获利,市政府每周至少需要补贴1125元才能不亏损.
19.解析:(1)在中,因为,
由余弦定理,得,
所以.
在中,由正弦定理,
得,
所以.
(2)在中,因为,所以为钝角,
而,所以C为锐角.
故,则.
因为,所以,
.
从而
.
20.解析:(1)因为的增长速度越来越快,
而的增长速度越来越慢,
所以依题意应选择,
则有解得所以.
(2)当时,,设经过x个月,该水域中此生物的覆盖面积是当初投放时的1000倍,
则,
解得.
故约经过17个月后该水域中此生物的覆盖面积是当初投放时的1000倍.
21.解析:(1)函数的周期为.
(2)令,,
得,,
当时,,
当时,.
,
函数在上的单调增区间为,.
同理,函数在上的单调减区间为.
(3),
,,
可化为,
要想不等式恒成立,只需即可.
,
,.
22.解析:(1)证明:,
任取,,且,
则
,
函数在R上单调递增,
,即,
又,,
,
,
,
函数在R上单调递增.
(2)设,则,
,恒成立,即,恒成立,
即,令,
易得在上单调递减,在上单调递增,
又,,
的最大值为,
,即,
实数a的取值范围为.
(3)函数在上有两个零点且的图象的对称轴为直线,
解得.
实数a的取值范围为.
高一下学期
开学摸底考试试卷二卷
【考试用时:120分钟】【满分:150分】
考试范围:人教A版(2019)必修第一册(占比80%)+人教A版(2019)必修第二册第六章(占比20%)
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作答无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知命题,,则命题p的否定为( )
A.,
B.,
C.,
D.,
2.若集合,或,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若,则( )
A.无最大值,有最小值8 B.无最大值,有最小值-4
C.有最大值8,有最小值-4 D.有最大值-4,无最小值
4.在中,内角A,B,C的对边分别为a,b,c,若,则的外接圆的面积为( )
A. B. C. D.
5.函数的大致图象是( )
A. B.
C. D.
6.已知为第三象限角,且,,则m的值为( )
A. B. C. D.
7.已知函数,,的零点分别为a,b,c,则( )
A. B. C. D.
8.已知函数,若使得在区间上为增函数的整数有且仅有一个,则实数的取值范围是( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列说法正确的是( )
A.“对任意一个无理数x,也是无理数”是真命题
B.“”是“”的充要条件
C.命题“,”的否定是“,”
D.若“”的一个必要不充分条件是“”,则实数m的取值范围是
10.设函数,对于任意的,,下列式子成立的是( )
A. B.
C. D.
11.已知向量在同一平面内且两两不共线,则下列命题为真命题的是( )
A.给定向量,总存在向量,使
B.给定向量,总存在实数和,使
C.给定向量,单位向量,正实数,总存在单位向量和实数,使
D.若,且存在单位向量和正实数,使,则
12.已知函数的图象关于点中心对称,且与直线的两个相邻交点间的距离为,则下列叙述正确的是( )
A.函数的最小正周期为
B.函数图象的对称中心为
C.函数的图象可由的图象向左平移个单位长度得到
D.函数的单调递增区间为
三、填空题:本题共4小题,每小题5分,共20分.
13.已知,且,则__________,____________.
14.如图,在中,M为边BC上不同于B,C的任意一点,点N满足.若,则的最小值为___________.
15.若对任意,恒成立,则a的取值范围为____________.
16.已知函数若方程有4个不同的实数根,,,,则的取值范围是____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知集合,或.
(1)当时,求;
(2)若“”是“”的充分不必要条件,且,求实数a的取值范围.
18.(12分)《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(1)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(2)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则市政府至少需要补贴多少元才能使该企业不亏损?
19. (12分)在中,角A,B,C的对边分别为a,b,c.已知.
(1)求的值;
(2)在边BC上取一点D,使得,求的值.
20. (12分)某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快,开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积y(单位:平方米)与经过月份的关系有两个函数模型与可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的覆盖面积是当初投放时的1000倍?(参考数据:,,,)
21. (12分)已知函数.
(1)求函数的周期;
(2)求函数在上的单调区间;
(3)若对任意,不等式恒成立,试求m的取值范围.
22. (12分)已知函数.
(1)当时,设,证明:函数在R上单调递增;
(2)若,恒成立,求实数a的取值范围;
(3)若函数在上有两个零点,求实数a的取值范围.
答案以及解析
1.答案:C
解析:在中,量词“”改为“”,结论“”改为“”,故选C.
2.答案:A
解析:或,
,
,但.
故“”是“”的充分不必要条件.
3.答案:D
解析:若,则,,当且仅当,即时等号成立,,有最大值-4,没有最小值.故选D.
4.答案:B
解析:在中,,所以.设的外接圆的半径为R,则由正弦定理,可得,解得,故的外接圆的面积,故选B.
5.答案:D
解析:易知函数是偶函数,排除选项B,C;当时,,对应点在第四象限,故排除A.故选D.
6.答案:B
解析:依题意得,
又,.
由是第三象限角知,,
,故选B.
7.答案:B
解析:函数的零点为函数与的图象交点的横坐标,函数的零点为函数与的图象交点的横坐标,
函数的零点为函数与的图象交点的横坐标,
在同一直角坐标系内作出函数,,与的图象如图所示:
由图可知:,,,,故选B.
8.答案:D
解析:因为在区间上为增函数,
所以,
可得.
当时,满足条件的整数可为1或2,不满足题意,舍去.
当时,由,知,所以,
所以有,即,
要使整数有且仅有一个,需,
解得.
综上,实数的取值范围为,故选D.
9.答案:CD
解析:是无理数,是有理数,故A错;
,时,,但,不是充要条件,故B错;
命题“,”的否定是“,”,故C正确;
若“”的一个必要不充分条件是“”,则且两个等号不同时取得,解得,故D正确.故选CD.
10.答案:ACD
解析:,,所以A成立;,,所以B不成立;易知函数在R上是单调递增函数,则,所以C成立;说明函数图象是下凹的,而函数图象是下凹的,所以D成立.故选ACD.
11.答案:ABD
解析:给定向量,显然存在向量,使,即,所以A是真命题.由平面向量的基本定理可得B是真命题.C选项中,取,设,则,即,解得,因为为单位向量,所以,所以C不是真命题.D选项中,,且向量的模都为1,又两两不共线,所以由三角形的三边关系可得,即.又,所以D是真命题.故选ABD.
12.答案:ACD
解析:对于A,根据与直线的两个相邻交点间的距离可知最小正周期,所以A正确;对于B,,又为图象的一个对称中心,所以,得,因为,所以,,令,得,所以函数图象的对称中心为,B错误;对于C,,则的图象可由函数的图象向左平移个单位长度得到,C正确;对于D,令,得,D正确.
13.答案:;
解析:由得,
所以,
所以
.
14.答案:
解析:根据题意,得.
因为三点共线,所以有,即,,所以,所以当时,取得最小值,为.
15.答案:
解析:,,根据题意知.
,
.
,(当且仅当时取等号),
,.
16.答案:
解析:作出函数的图象如图所示.
由方程有4个解,知,且.
由得.
由,关于直线对称,得,
.
,,,
.
因此的取值范围是.
17.答案:(1) 或.
(2).
解析:(1)当时,,
又或,
或.
(2)或,
.
由“”是“”的充分不必要条件,
得,
又,,
.
的取值范围是.
18.解析:(1)由题意可知,
每吨产品的平均加工处理成本为,
当且仅当,即(吨)时,才能使每吨产品的平均加工处理成本最低.
(2)设该企业每周获利为s元,则,
,当时,.
故该企业每周不能获利,市政府每周至少需要补贴1125元才能不亏损.
19.解析:(1)在中,因为,
由余弦定理,得,
所以.
在中,由正弦定理,
得,
所以.
(2)在中,因为,所以为钝角,
而,所以C为锐角.
故,则.
因为,所以,
.
从而
.
20.解析:(1)因为的增长速度越来越快,
而的增长速度越来越慢,
所以依题意应选择,
则有解得所以.
(2)当时,,设经过x个月,该水域中此生物的覆盖面积是当初投放时的1000倍,
则,
解得.
故约经过17个月后该水域中此生物的覆盖面积是当初投放时的1000倍.
21.解析:(1)函数的周期为.
(2)令,,
得,,
当时,,
当时,.
,
函数在上的单调增区间为,.
同理,函数在上的单调减区间为.
(3),
,,
可化为,
要想不等式恒成立,只需即可.
,
,.
22.解析:(1)证明:,
任取,,且,
则
,
函数在R上单调递增,
,即,
又,,
,
,
,
函数在R上单调递增.
(2)设,则,
,恒成立,即,恒成立,
即,令,
易得在上单调递减,在上单调递增,
又,,
的最大值为,
,即,
实数a的取值范围为.
(3)函数在上有两个零点且的图象的对称轴为直线,
解得.
实数a的取值范围为.
同课章节目录
