2021-2022学年人教版九年级数学下册第二十七章相似易错题型(Word版,附答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章相似易错题型(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 372.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 20:34:43 | ||
图片预览



文档简介
人教版九年级数学下册第二十七章 相似 易错题型
27.1 图形的相似
易错点1 判断两个多边形相似时易出错
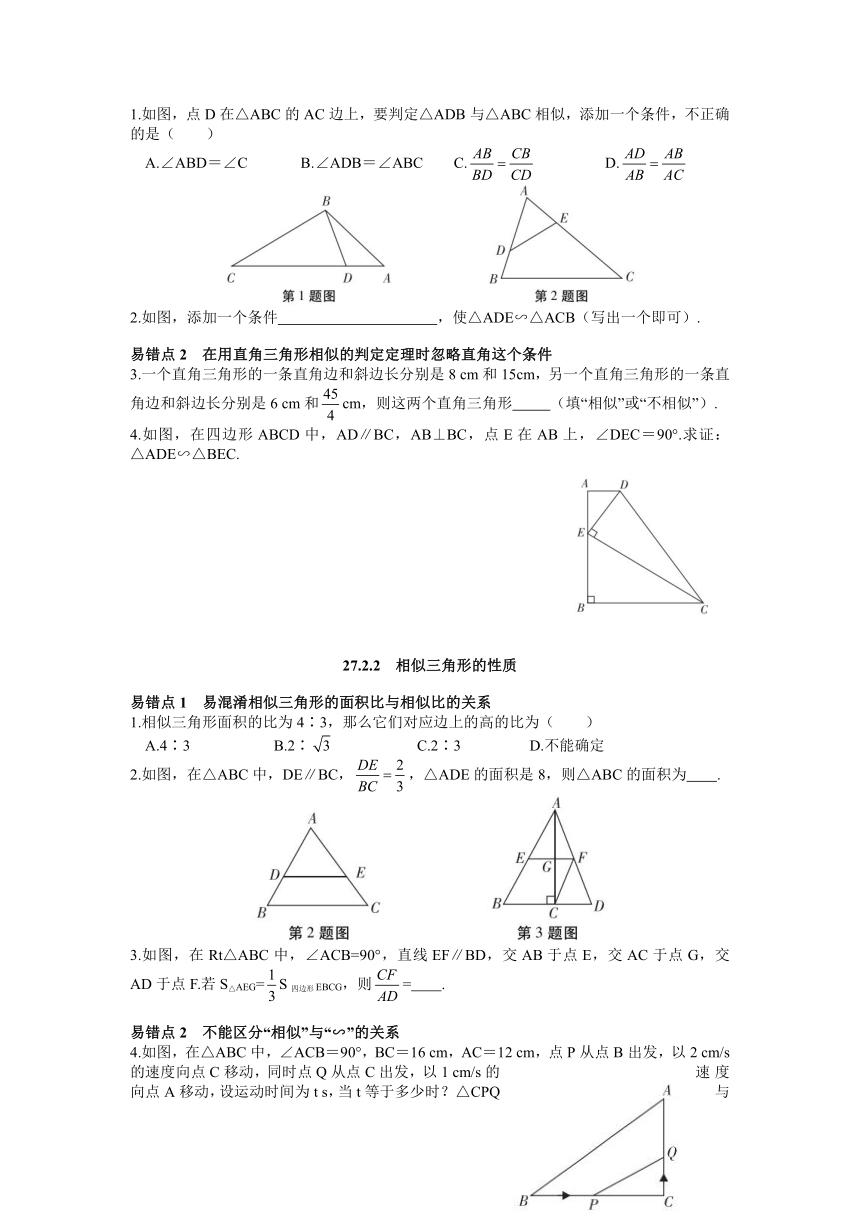
1.如图,一张矩形纸片ABCD的长BC=x cm,宽AB=y cm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则的值为( )
A. B. C. D.
2.如图,在四边形ABCD与四边形EFGH中,∠A=70°,∠B=80°,∠C=110°,∠F=80°,∠G=110°,∠H=100°,则四边形ABCD与四边形EFGH (填“一定相似”或“不一定相似”).
3.如图,它们是两个相似的平行四边形,根据条件可知,∠α= ,m= .
易错点2 求线段比例时,忽略单位的统一
4.A,B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5 000 C.500:1 D.5 000:1
5.比例尺为1∶1 000的图纸上某区域面积400 cm2,则实际面积为( )
A.4×105 m2? B.4×104 m2?
C.1.6×105 m2? D.2×104 m2?
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例的基本事实
易错点1 运用平行线分线段成比例时易混淆比例线段的对应关系
1.如图所示,已知DE∥BC,EF∥AB,下列比例式正确的个数是( )
①;②;③.
A.3个 B.2个 C.1个 D.0个
2.如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( )
A. B. C. D.
易错点2 运用平行线分线段成比例计算时,忽视平行线的位置而漏解
3.在△ABC中,AB=6,AC=9,点D在边AB所在的直线上,且AD=2,过点D作DE∥BC交边AC所在直线于点E,则CE的长为 .
4.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.若AC=6,DE=4,则DF= .
第2课时 相似三角形的判定定理1,2
易错点 误认为两边成比例且有一组对应角相等的两个三角形相似
1.如图,==,B,D,E三点共线,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
2.在△ABC和△DEF中,∠A=∠D,=,那么△ABC和△DEF (填“一定相似”或“不一定相似”).
3.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
4.如图,在△ABC中,AC=8 cm,BC=16 cm,点P从点A出发,沿着AC边向点C以1 cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2 cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC与△ABC相似?
第3课时 相似三角形的判定定理3
易错点1 证相似时易忽视图形中隐含的条件
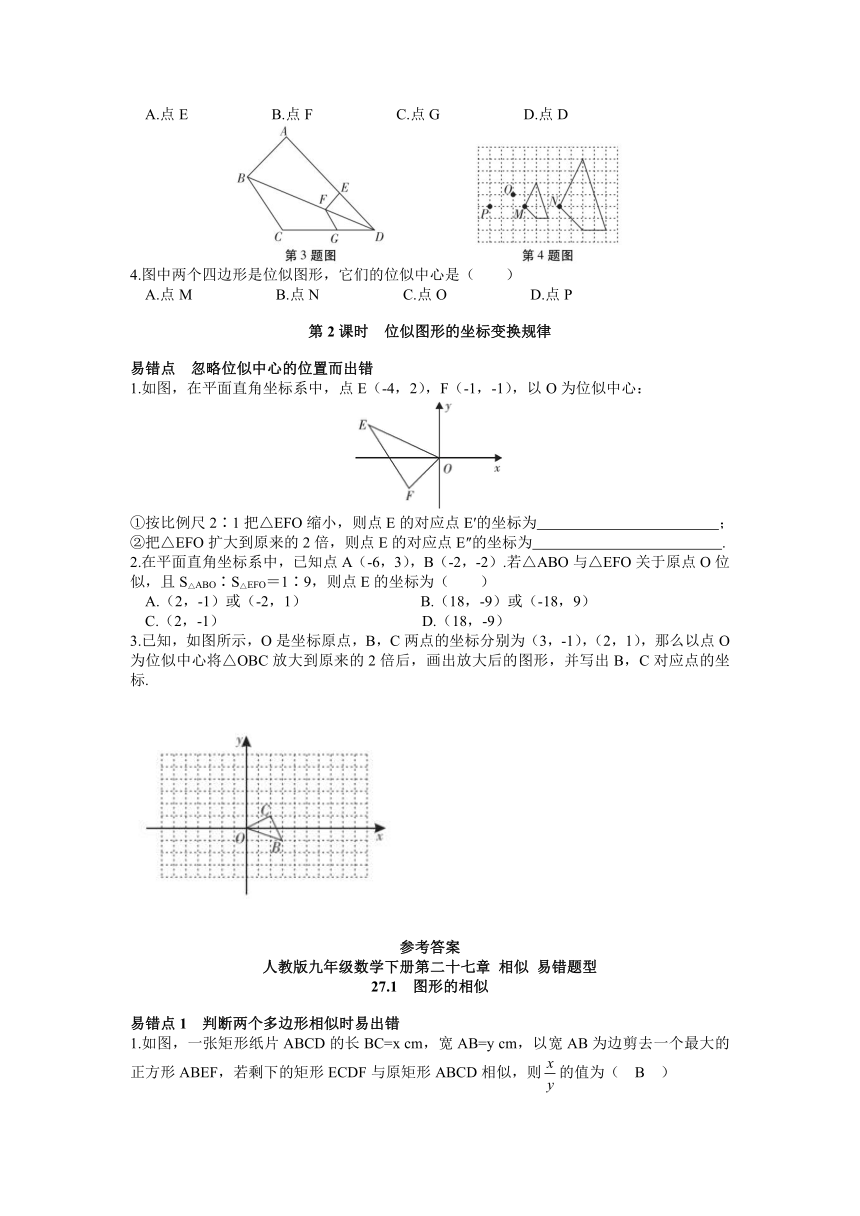
1.如图,点D在△ABC的AC边上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
2.如图,添加一个条件 ,使△ADE∽△ACB(写出一个即可).
易错点2 在用直角三角形相似的判定定理时忽略直角这个条件
3.一个直角三角形的一条直角边和斜边长分别是8 cm和15cm,另一个直角三角形的一条直角边和斜边长分别是6 cm和cm,则这两个直角三角形 (填“相似”或“不相似”).
4.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.求证:△ADE∽△BEC.
27.2.2 相似三角形的性质
易错点1 易混淆相似三角形的面积比与相似比的关系
1.相似三角形面积的比为4∶3,那么它们对应边上的高的比为( )
A.4∶3 B.2∶ C.2∶3 D.不能确定
2.如图,在△ABC中,DE∥BC,,△ADE的面积是8,则△ABC的面积为 .
3.如图,在Rt△ABC中,∠ACB=90°,直线EF∥BD,交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则= .
易错点2 不能区分“相似”与“∽”的关系
4.如图,在△ABC中,∠ACB=90°,BC=16 cm,AC=12 cm,点P从点B出发,以2 cm/s的速度向点C移动,同时点Q从点C出发,以1 cm/s的速度向点A移动,设运动时间为t s,当t等于多少时?△CPQ与△ABC相似.
27.2.3 相似三角形应用举例
易错点 利用光线与影子测物体的高度时找错对应关系
1.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为( )
A.10 m B.12 m C.15 m D.40 m
2.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF保持水平,并且边DE与点B 在同一直线上.已知纸板的两条直角边DE=0.4 m,EF=0.2 m,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高.
3.小亮在某一时刻测得小树的高为1.5 m,其影长为1.2 m,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,它的一部分影子便落在了教学楼的墙上,经测量,地面部分的影长为6.4 m,墙上的影长为2 m,那么这棵大树的高为多少m
27.3 位似
第1课时 位似图形的概念及画法
易错点1 忽略位似图形满足的条件而出错
1.如图,在平行四边形ABCD中,点E,F分别是边AB,CD的中点,点O是AF,DE的交点,点P是BF,CE的交点,除△FOD外,与△AOE位似的是 (写出一个即可).
2.如图,正方形 EFGH,IJKL是由正方形ABCD经过位似变换得到的,点Р是位似中心.
(1)如果相似比为3,正方形ABCD的位似图形是 ;
(2)正方形IJKL是正方形EFGH的位似图形吗
答: .如果是,那么相似比为 ;
(3)如果由正方形EFGH得到它的位似图形正方形ABCD,那么相似比为 .
易错点2 不能正确确定位似中心
3.四边形ABCD和四边形EFGD是位似图形,它们的位似中心是( )
A.点E B.点F C.点G D.点D
4.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
第2课时 位似图形的坐标变换规律
易错点 忽略位似中心的位置而出错
1.如图,在平面直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心:
①按比例尺2∶1把△EFO缩小,则点E的对应点E′的坐标为 ;
②把△EFO扩大到原来的2倍,则点E的对应点E″的坐标为 .
2.在平面直角坐标系中,已知点A(-6,3),B(-2,-2).若△ABO与△EFO关于原点O位似,且S△ABO∶S△EFO=1∶9,则点E的坐标为( )
A.(2,-1)或(-2,1) B.(18,-9)或(-18,9)
C.(2,-1) D.(18,-9)
3.已知,如图所示,O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1),那么以点O为位似中心将△OBC放大到原来的2倍后,画出放大后的图形,并写出B,C对应点的坐标.
参考答案
人教版九年级数学下册第二十七章 相似 易错题型
27.1 图形的相似
易错点1 判断两个多边形相似时易出错
1.如图,一张矩形纸片ABCD的长BC=x cm,宽AB=y cm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则的值为( B )
A. B. C. D.
2.如图,在四边形ABCD与四边形EFGH中,∠A=70°,∠B=80°,∠C=110°,∠F=80°,∠G=110°,∠H=100°,则四边形ABCD与四边形EFGH 不一定相似 (填“一定相似”或“不一定相似”).
3.如图,它们是两个相似的平行四边形,根据条件可知,∠α= 125° ,m= 12 .
易错点2 求线段比例时,忽略单位的统一
4.A,B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( B )
A.1:500 B.1:5 000 C.500:1 D.5 000:1
5.比例尺为1∶1 000的图纸上某区域面积400 cm2,则实际面积为( B )
A.4×105 m2? B.4×104 m2?
C.1.6×105 m2? D.2×104 m2?
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例的基本事实
易错点1 运用平行线分线段成比例时易混淆比例线段的对应关系
1.如图所示,已知DE∥BC,EF∥AB,下列比例式正确的个数是( C )
①;②;③.
A.3个 B.2个 C.1个 D.0个
2.如图,F是ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( A )
A. B. C. D.
易错点2 运用平行线分线段成比例计算时,忽视平行线的位置而漏解
3.在△ABC中,AB=6,AC=9,点D在边AB所在的直线上,且AD=2,过点D作DE∥BC交边AC所在直线于点E,则CE的长为 6或12 .
4.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.若AC=6,DE=4,则DF= 2或10 .
第2课时 相似三角形的判定定理1,2
易错点 误认为两边成比例且有一组对应角相等的两个三角形相似
1.如图,==,B,D,E三点共线,则图中相似三角形共有( C )
A.1对 B.2对 C.3对 D.4对
2.在△ABC和△DEF中,∠A=∠D,=,那么△ABC和△DEF 不一定相似 (填“一定相似”或“不一定相似”).
3.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
解:∵==,,
∴=.
又∵∠A=∠B,∴△AED∽△BFC.
∴=,即=.解得CF=7.5.
4.如图,在△ABC中,AC=8 cm,BC=16 cm,点P从点A出发,沿着AC边向点C以1 cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2 cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC与△ABC相似?
解:设经过x秒,两三角形相似,则AP=x,CP=8-x,CQ=2x,
①当CP与CA是对应边时,
,即.解得x=4;
②当CP与BC是对应边时,
,即.解得x=.
? 综上所述,经过4 s或s,△PQC与△ABC相似.
第3课时 相似三角形的判定定理3
易错点1 证相似时易忽视图形中隐含的条件
1.如图,点D在△ABC的AC边上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( C )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
2.如图,添加一个条件 (答案不唯一) ,使△ADE∽△ACB(写出一个即可).
易错点2 在用直角三角形相似的判定定理时忽略直角这个条件
3.一个直角三角形的一条直角边和斜边长分别是8 cm和15cm,另一个直角三角形的一条直角边和斜边长分别是6 cm和cm,则这两个直角三角形 相似 (填“相似”或“不相似”).
4.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.求证:△ADE∽△BEC.
证明:∵AD∥BC,AB⊥BC,
∴AB⊥AD,∠A=∠B=90°.
∴∠ADE+∠AED=90°.
∵∠DEC=90°,
∴∠AED+∠BEC=90°.
∴∠ADE=∠BEC.
∴△ADE∽△BEC.
27.2.2 相似三角形的性质
易错点1 易混淆相似三角形的面积比与相似比的关系
1.相似三角形面积的比为4∶3,那么它们对应边上的高的比为( B )
A.4∶3 B.2∶ C.2∶3 D.不能确定
2.如图,在△ABC中,DE∥BC,,△ADE的面积是8,则△ABC的面积为 18 .
3.如图,在Rt△ABC中,∠ACB=90°,直线EF∥BD,交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则= .
易错点2 不能区分“相似”与“∽”的关系
4.如图,在△ABC中,∠ACB=90°,BC=16 cm,AC=12 cm,点P从点B出发,以2 cm/s的速度向点C移动,同时点Q从点C出发,以1 cm/s的速度向点A移动,设运动时间为t s,当t等于多少时?△CPQ与△ABC相似.
解:①当CP与CB是对应边时,
△CPQ∽△CBA,∴,
即.解得t=;
②当CP与CA是对应边时,
△CPQ∽△CAB,∴,
即.解得t=.
综上所述,当t= s或 s时,△CPQ与△CBA相似.
27.2.3 相似三角形应用举例
易错点 利用光线与影子测物体的高度时找错对应关系
1.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为( C )
A.10 m B.12 m C.15 m D.40 m
2.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF保持水平,并且边DE与点B 在同一直线上.已知纸板的两条直角边DE=0.4 m,EF=0.2 m,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高.
解:∵∠DEF=∠DCB=90°,
∠D=∠D,
∴△DEF∽△DCB.
∴,即.
解得CB=4.
∴AB=AC+BC=1.5+4=5.5(米).
答:树高为5.5米.
3.小亮在某一时刻测得小树的高为1.5 m,其影长为1.2 m,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,它的一部分影子便落在了教学楼的墙上,经测量,地面部分的影长为6.4 m,墙上的影长为2 m,那么这棵大树的高为多少m
解:设落在教学楼墙上部分的影长为x m,则
.解得x=1.6.
设树高为y m,则
,解得y=10.
答:树高为10 m.
27.3 位似
第1课时 位似图形的概念及画法
易错点1 忽略位似图形满足的条件而出错
1.如图,在平行四边形ABCD中,点E,F分别是边AB,CD的中点,点O是AF,DE的交点,点P是BF,CE的交点,除△FOD外,与△AOE位似的是 △AFB(或△CPF) (写出一个即可).
2.如图,正方形 EFGH,IJKL是由正方形ABCD经过位似变换得到的,点Р是位似中心.
(1)如果相似比为3,正方形ABCD的位似图形是 正方形IJKL ;
(2)正方形IJKL是正方形EFGH的位似图形吗
答: 是 .如果是,那么相似比为 3∶2 ;
(3)如果由正方形EFGH得到它的位似图形正方形ABCD,那么相似比为 2∶1 .
易错点2 不能正确确定位似中心
3.四边形ABCD和四边形EFGD是位似图形,它们的位似中心是( D )
A.点E B.点F C.点G D.点D
4.图中两个四边形是位似图形,它们的位似中心是( D )
A.点M B.点N C.点O D.点P
第2课时 位似图形的坐标变换规律
易错点 忽略位似中心的位置而出错
1.如图,在平面直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心:
①按比例尺2∶1把△EFO缩小,则点E的对应点E′的坐标为 (2,-1)或(-2,1) ;
②把△EFO扩大到原来的2倍,则点E的对应点E″的坐标为 (8,-4)或(-8,4) .
2.在平面直角坐标系中,已知点A(-6,3),B(-2,-2).若△ABO与△EFO关于原点O位似,且S△ABO∶S△EFO=1∶9,则点E的坐标为( B )
A.(2,-1)或(-2,1) B.(18,-9)或(-18,9)
C.(2,-1) D.(18,-9)
3.已知,如图所示,O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1),那么以点O为位似中心将△OBC放大到原来的2倍后,画出放大后的图形,并写出B,C对应点的坐标.
解:放大后的图形△OB1 C1和△OB2C2如图所示,此时B1(6,-2),C1(4,2)或B2(-6,2),C2(-4,-2).
27.1 图形的相似
易错点1 判断两个多边形相似时易出错
1.如图,一张矩形纸片ABCD的长BC=x cm,宽AB=y cm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则的值为( )
A. B. C. D.
2.如图,在四边形ABCD与四边形EFGH中,∠A=70°,∠B=80°,∠C=110°,∠F=80°,∠G=110°,∠H=100°,则四边形ABCD与四边形EFGH (填“一定相似”或“不一定相似”).
3.如图,它们是两个相似的平行四边形,根据条件可知,∠α= ,m= .
易错点2 求线段比例时,忽略单位的统一
4.A,B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5 000 C.500:1 D.5 000:1
5.比例尺为1∶1 000的图纸上某区域面积400 cm2,则实际面积为( )
A.4×105 m2? B.4×104 m2?
C.1.6×105 m2? D.2×104 m2?
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例的基本事实
易错点1 运用平行线分线段成比例时易混淆比例线段的对应关系
1.如图所示,已知DE∥BC,EF∥AB,下列比例式正确的个数是( )
①;②;③.
A.3个 B.2个 C.1个 D.0个
2.如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( )
A. B. C. D.
易错点2 运用平行线分线段成比例计算时,忽视平行线的位置而漏解
3.在△ABC中,AB=6,AC=9,点D在边AB所在的直线上,且AD=2,过点D作DE∥BC交边AC所在直线于点E,则CE的长为 .
4.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.若AC=6,DE=4,则DF= .
第2课时 相似三角形的判定定理1,2
易错点 误认为两边成比例且有一组对应角相等的两个三角形相似
1.如图,==,B,D,E三点共线,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
2.在△ABC和△DEF中,∠A=∠D,=,那么△ABC和△DEF (填“一定相似”或“不一定相似”).
3.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
4.如图,在△ABC中,AC=8 cm,BC=16 cm,点P从点A出发,沿着AC边向点C以1 cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2 cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC与△ABC相似?
第3课时 相似三角形的判定定理3
易错点1 证相似时易忽视图形中隐含的条件
1.如图,点D在△ABC的AC边上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
2.如图,添加一个条件 ,使△ADE∽△ACB(写出一个即可).
易错点2 在用直角三角形相似的判定定理时忽略直角这个条件
3.一个直角三角形的一条直角边和斜边长分别是8 cm和15cm,另一个直角三角形的一条直角边和斜边长分别是6 cm和cm,则这两个直角三角形 (填“相似”或“不相似”).
4.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.求证:△ADE∽△BEC.
27.2.2 相似三角形的性质
易错点1 易混淆相似三角形的面积比与相似比的关系
1.相似三角形面积的比为4∶3,那么它们对应边上的高的比为( )
A.4∶3 B.2∶ C.2∶3 D.不能确定
2.如图,在△ABC中,DE∥BC,,△ADE的面积是8,则△ABC的面积为 .
3.如图,在Rt△ABC中,∠ACB=90°,直线EF∥BD,交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则= .
易错点2 不能区分“相似”与“∽”的关系
4.如图,在△ABC中,∠ACB=90°,BC=16 cm,AC=12 cm,点P从点B出发,以2 cm/s的速度向点C移动,同时点Q从点C出发,以1 cm/s的速度向点A移动,设运动时间为t s,当t等于多少时?△CPQ与△ABC相似.
27.2.3 相似三角形应用举例
易错点 利用光线与影子测物体的高度时找错对应关系
1.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为( )
A.10 m B.12 m C.15 m D.40 m
2.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF保持水平,并且边DE与点B 在同一直线上.已知纸板的两条直角边DE=0.4 m,EF=0.2 m,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高.
3.小亮在某一时刻测得小树的高为1.5 m,其影长为1.2 m,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,它的一部分影子便落在了教学楼的墙上,经测量,地面部分的影长为6.4 m,墙上的影长为2 m,那么这棵大树的高为多少m
27.3 位似
第1课时 位似图形的概念及画法
易错点1 忽略位似图形满足的条件而出错
1.如图,在平行四边形ABCD中,点E,F分别是边AB,CD的中点,点O是AF,DE的交点,点P是BF,CE的交点,除△FOD外,与△AOE位似的是 (写出一个即可).
2.如图,正方形 EFGH,IJKL是由正方形ABCD经过位似变换得到的,点Р是位似中心.
(1)如果相似比为3,正方形ABCD的位似图形是 ;
(2)正方形IJKL是正方形EFGH的位似图形吗
答: .如果是,那么相似比为 ;
(3)如果由正方形EFGH得到它的位似图形正方形ABCD,那么相似比为 .
易错点2 不能正确确定位似中心
3.四边形ABCD和四边形EFGD是位似图形,它们的位似中心是( )
A.点E B.点F C.点G D.点D
4.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
第2课时 位似图形的坐标变换规律
易错点 忽略位似中心的位置而出错
1.如图,在平面直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心:
①按比例尺2∶1把△EFO缩小,则点E的对应点E′的坐标为 ;
②把△EFO扩大到原来的2倍,则点E的对应点E″的坐标为 .
2.在平面直角坐标系中,已知点A(-6,3),B(-2,-2).若△ABO与△EFO关于原点O位似,且S△ABO∶S△EFO=1∶9,则点E的坐标为( )
A.(2,-1)或(-2,1) B.(18,-9)或(-18,9)
C.(2,-1) D.(18,-9)
3.已知,如图所示,O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1),那么以点O为位似中心将△OBC放大到原来的2倍后,画出放大后的图形,并写出B,C对应点的坐标.
参考答案
人教版九年级数学下册第二十七章 相似 易错题型
27.1 图形的相似
易错点1 判断两个多边形相似时易出错
1.如图,一张矩形纸片ABCD的长BC=x cm,宽AB=y cm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则的值为( B )
A. B. C. D.
2.如图,在四边形ABCD与四边形EFGH中,∠A=70°,∠B=80°,∠C=110°,∠F=80°,∠G=110°,∠H=100°,则四边形ABCD与四边形EFGH 不一定相似 (填“一定相似”或“不一定相似”).
3.如图,它们是两个相似的平行四边形,根据条件可知,∠α= 125° ,m= 12 .
易错点2 求线段比例时,忽略单位的统一
4.A,B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( B )
A.1:500 B.1:5 000 C.500:1 D.5 000:1
5.比例尺为1∶1 000的图纸上某区域面积400 cm2,则实际面积为( B )
A.4×105 m2? B.4×104 m2?
C.1.6×105 m2? D.2×104 m2?
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例的基本事实
易错点1 运用平行线分线段成比例时易混淆比例线段的对应关系
1.如图所示,已知DE∥BC,EF∥AB,下列比例式正确的个数是( C )
①;②;③.
A.3个 B.2个 C.1个 D.0个
2.如图,F是ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( A )
A. B. C. D.
易错点2 运用平行线分线段成比例计算时,忽视平行线的位置而漏解
3.在△ABC中,AB=6,AC=9,点D在边AB所在的直线上,且AD=2,过点D作DE∥BC交边AC所在直线于点E,则CE的长为 6或12 .
4.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.若AC=6,DE=4,则DF= 2或10 .
第2课时 相似三角形的判定定理1,2
易错点 误认为两边成比例且有一组对应角相等的两个三角形相似
1.如图,==,B,D,E三点共线,则图中相似三角形共有( C )
A.1对 B.2对 C.3对 D.4对
2.在△ABC和△DEF中,∠A=∠D,=,那么△ABC和△DEF 不一定相似 (填“一定相似”或“不一定相似”).
3.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
解:∵==,,
∴=.
又∵∠A=∠B,∴△AED∽△BFC.
∴=,即=.解得CF=7.5.
4.如图,在△ABC中,AC=8 cm,BC=16 cm,点P从点A出发,沿着AC边向点C以1 cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2 cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC与△ABC相似?
解:设经过x秒,两三角形相似,则AP=x,CP=8-x,CQ=2x,
①当CP与CA是对应边时,
,即.解得x=4;
②当CP与BC是对应边时,
,即.解得x=.
? 综上所述,经过4 s或s,△PQC与△ABC相似.
第3课时 相似三角形的判定定理3
易错点1 证相似时易忽视图形中隐含的条件
1.如图,点D在△ABC的AC边上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( C )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
2.如图,添加一个条件 (答案不唯一) ,使△ADE∽△ACB(写出一个即可).
易错点2 在用直角三角形相似的判定定理时忽略直角这个条件
3.一个直角三角形的一条直角边和斜边长分别是8 cm和15cm,另一个直角三角形的一条直角边和斜边长分别是6 cm和cm,则这两个直角三角形 相似 (填“相似”或“不相似”).
4.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.求证:△ADE∽△BEC.
证明:∵AD∥BC,AB⊥BC,
∴AB⊥AD,∠A=∠B=90°.
∴∠ADE+∠AED=90°.
∵∠DEC=90°,
∴∠AED+∠BEC=90°.
∴∠ADE=∠BEC.
∴△ADE∽△BEC.
27.2.2 相似三角形的性质
易错点1 易混淆相似三角形的面积比与相似比的关系
1.相似三角形面积的比为4∶3,那么它们对应边上的高的比为( B )
A.4∶3 B.2∶ C.2∶3 D.不能确定
2.如图,在△ABC中,DE∥BC,,△ADE的面积是8,则△ABC的面积为 18 .
3.如图,在Rt△ABC中,∠ACB=90°,直线EF∥BD,交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则= .
易错点2 不能区分“相似”与“∽”的关系
4.如图,在△ABC中,∠ACB=90°,BC=16 cm,AC=12 cm,点P从点B出发,以2 cm/s的速度向点C移动,同时点Q从点C出发,以1 cm/s的速度向点A移动,设运动时间为t s,当t等于多少时?△CPQ与△ABC相似.
解:①当CP与CB是对应边时,
△CPQ∽△CBA,∴,
即.解得t=;
②当CP与CA是对应边时,
△CPQ∽△CAB,∴,
即.解得t=.
综上所述,当t= s或 s时,△CPQ与△CBA相似.
27.2.3 相似三角形应用举例
易错点 利用光线与影子测物体的高度时找错对应关系
1.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为( C )
A.10 m B.12 m C.15 m D.40 m
2.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF保持水平,并且边DE与点B 在同一直线上.已知纸板的两条直角边DE=0.4 m,EF=0.2 m,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高.
解:∵∠DEF=∠DCB=90°,
∠D=∠D,
∴△DEF∽△DCB.
∴,即.
解得CB=4.
∴AB=AC+BC=1.5+4=5.5(米).
答:树高为5.5米.
3.小亮在某一时刻测得小树的高为1.5 m,其影长为1.2 m,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,它的一部分影子便落在了教学楼的墙上,经测量,地面部分的影长为6.4 m,墙上的影长为2 m,那么这棵大树的高为多少m
解:设落在教学楼墙上部分的影长为x m,则
.解得x=1.6.
设树高为y m,则
,解得y=10.
答:树高为10 m.
27.3 位似
第1课时 位似图形的概念及画法
易错点1 忽略位似图形满足的条件而出错
1.如图,在平行四边形ABCD中,点E,F分别是边AB,CD的中点,点O是AF,DE的交点,点P是BF,CE的交点,除△FOD外,与△AOE位似的是 △AFB(或△CPF) (写出一个即可).
2.如图,正方形 EFGH,IJKL是由正方形ABCD经过位似变换得到的,点Р是位似中心.
(1)如果相似比为3,正方形ABCD的位似图形是 正方形IJKL ;
(2)正方形IJKL是正方形EFGH的位似图形吗
答: 是 .如果是,那么相似比为 3∶2 ;
(3)如果由正方形EFGH得到它的位似图形正方形ABCD,那么相似比为 2∶1 .
易错点2 不能正确确定位似中心
3.四边形ABCD和四边形EFGD是位似图形,它们的位似中心是( D )
A.点E B.点F C.点G D.点D
4.图中两个四边形是位似图形,它们的位似中心是( D )
A.点M B.点N C.点O D.点P
第2课时 位似图形的坐标变换规律
易错点 忽略位似中心的位置而出错
1.如图,在平面直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心:
①按比例尺2∶1把△EFO缩小,则点E的对应点E′的坐标为 (2,-1)或(-2,1) ;
②把△EFO扩大到原来的2倍,则点E的对应点E″的坐标为 (8,-4)或(-8,4) .
2.在平面直角坐标系中,已知点A(-6,3),B(-2,-2).若△ABO与△EFO关于原点O位似,且S△ABO∶S△EFO=1∶9,则点E的坐标为( B )
A.(2,-1)或(-2,1) B.(18,-9)或(-18,9)
C.(2,-1) D.(18,-9)
3.已知,如图所示,O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1),那么以点O为位似中心将△OBC放大到原来的2倍后,画出放大后的图形,并写出B,C对应点的坐标.
解:放大后的图形△OB1 C1和△OB2C2如图所示,此时B1(6,-2),C1(4,2)或B2(-6,2),C2(-4,-2).
