2019粤教版必修第三册第2章第二节带电粒子在电场中的运动(word版含答案)
文档属性
| 名称 | 2019粤教版必修第三册第2章第二节带电粒子在电场中的运动(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 376.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-18 07:38:22 | ||
图片预览




文档简介
2019粤教版必修第三册 第2章 第二节 带电粒子在电场中的运动
一、解答题
1.宇宙飞船进行长距离星际运行时,不能再用化学燃料,可采用一种新型发动机——离子发动机,小型高效的离子发动机所用燃料不到化学燃料发动机的,它可以使太空中的航天器获得动力,进而调整航天器的飞行姿态或飞行轨道。在离子发动机中,由电极发射的电子射入稀有气体(如氙气),使其离子化,然后从静止开始经电场加速后,从飞船尾部高速连续喷出,利用反冲使飞船本身得到加速。已知氙离子质量为m=2.2×10-25kg,电荷e=1.6×10-19C,加速电压U=275V。
(1)氙离子经电场加速后,获得的速度大小。
(2)为了使飞船得到F=3.0×10-2N的反冲力,求:
①每秒需要喷射出多少质量的氙离子;
②飞船向后喷出的氙离子形成的等效电流I。
2.在如图所示的示波管中,如果在荧光屏右上方出现亮斑,那么示波管中的X偏转板应带什么电?Y偏转板应带什么电?为什么?
3.如图所示,沿水平方向放置一条平直光滑槽,它垂直穿过开有小孔的两平行薄板,板相距3.5L。槽内有两个质量均为m的小球A和B,球A带电量为+2q,球B带电量为-3q,两球由长为2L的轻杆相连,组成一带电系统。最初A和B分别静止于左板的两侧,离板的距离均为L。若视小球为质点,不计轻杆的质量,在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成,不影响电场的分布),求:
(1)球B刚进入电场时,带电系统的速度大小;
(2)带电系统的A球是否能到达右板,说明理由?
(3)带电系统从开始运动到速度第一次为零时球B相对右板的位置?
4.飞行时间质谱仪通过探测不同离子到达探测头时间,可以测得离子比荷。如图甲所示,探测头在探测器左端中点。脉冲阀P喷出微量气体,经激光S照射产生不同价位的离子,假设正离子在A极板处初速度为零,AB极板间的加速电压为U0,离子加速后从B板小孔射出,沿中心线方向进入C、D板间的偏转控制区。已知加速电场AB间距为d,偏转极板CD的长度及宽度均为L。设加速电场和偏转电场均为匀强电场,不计离子重力和离子间相互作用。
(1)若偏转电压UCD=0,某比荷为k的离子沿中心线到达探测头,求该离子飞行总时间;
(2)若偏转电压UCD=0,在C、D板间加上垂直于纸面向里的匀强磁场,磁感应强度为B,要使所有离子均能通过控制区域并从右侧飞出,求这些离子比荷的取值范围;
(3)若偏转电压UCD与时间t的关系如图乙所示,最大值Um=4U0,周期,假设离子比荷为k,并且在t=0时刻开始连续均匀地射入偏转电场。以D极板的右端点为坐标原点,竖直向上为y轴正方向,探测头可在y轴上自由移动,在t=T到时间内,要使探测头能收集到所有粒子,求探测头坐标y随时间t变化的关系。
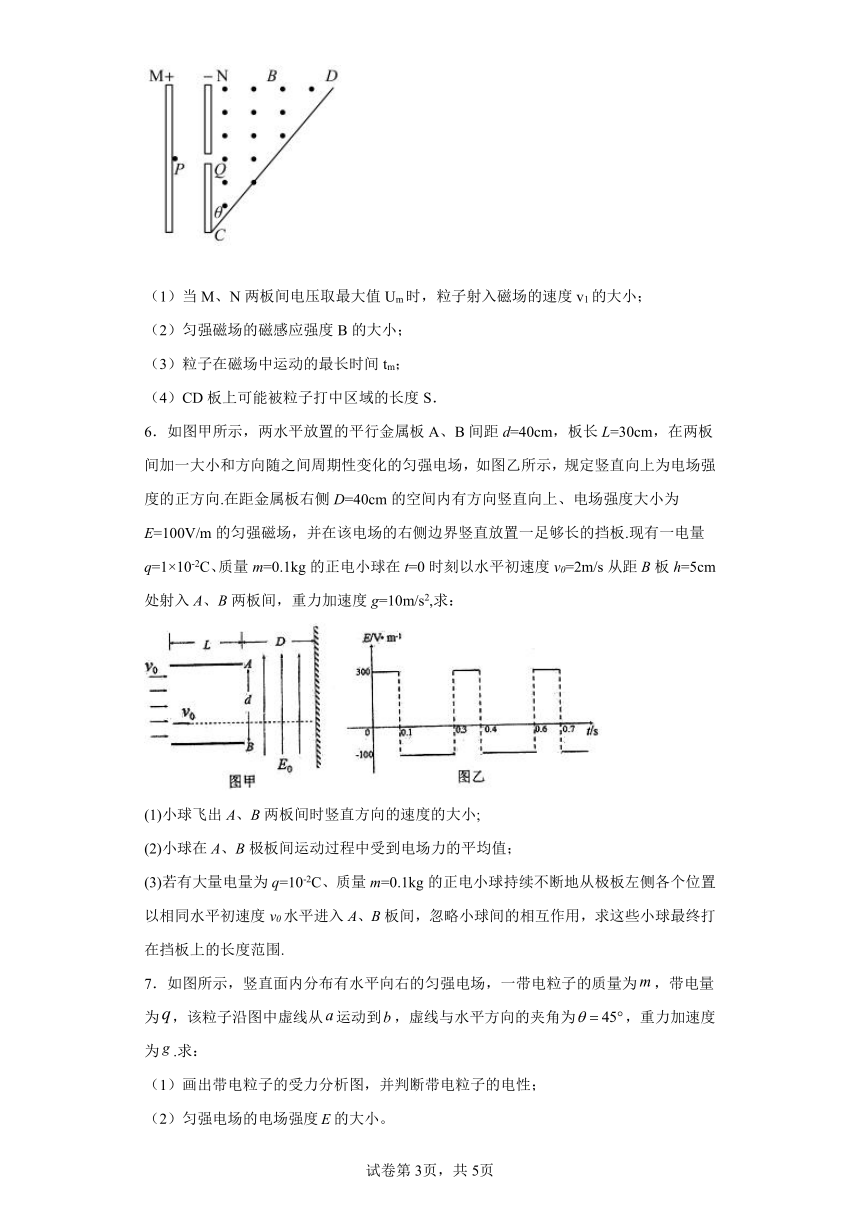
5.如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到最大值Um之间的各种数值.静止的带电粒子电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁场方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ= 45°,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上.求:
(1)当M、N两板间电压取最大值Um时,粒子射入磁场的速度v1的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)粒子在磁场中运动的最长时间tm;
(4)CD板上可能被粒子打中区域的长度S.
6.如图甲所示,两水平放置的平行金属板A、B间距d=40cm,板长L=30cm,在两板间加一大小和方向随之间周期性变化的匀强电场,如图乙所示,规定竖直向上为电场强度的正方向.在距金属板右侧D=40cm的空间内有方向竖直向上、电场强度大小为E=100V/m的匀强磁场,并在该电场的右侧边界竖直放置一足够长的挡板.现有一电量q=1×10-2C、质量m=0.1kg的正电小球在t=0时刻以水平初速度v0=2m/s从距B板h=5cm处射入A、B两板间,重力加速度g=10m/s2,求:
(1)小球飞出A、B两板间时竖直方向的速度的大小;
(2)小球在A、B极板间运动过程中受到电场力的平均值;
(3)若有大量电量为q=10-2C、质量m=0.1kg的正电小球持续不断地从极板左侧各个位置以相同水平初速度v0水平进入A、B板间,忽略小球间的相互作用,求这些小球最终打在挡板上的长度范围.
7.如图所示,竖直面内分布有水平向右的匀强电场,一带电粒子的质量为,带电量为,该粒子沿图中虚线从运动到,虚线与水平方向的夹角为,重力加速度为.求:
(1)画出带电粒子的受力分析图,并判断带电粒子的电性;
(2)匀强电场的电场强度的大小。
8.如图所示,倾角的光滑斜面固定在水平地面上,斜面顶端a离地高度,整个装置处于水平向左的匀强电场中,一个质量,带电量的物体(可视为质点)从斜面顶端静止释放,经过到达斜面底端b点(g取)。求:
(1)物体沿斜面下滑的加速度大小;
(2)电场强度E的大小(结果带根号);
(3)电场中a到b两点之间的电势差。
9.带电量为q,质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器,进入时速度和电容器中的场强方向垂直。已知:电容器的极板长为L,极板间距为d,两极板的电压为U2,重力不计,求:
(1)经过加速电场后的速度v0;
(2)离开电容器电场时的偏转量y;
(3)刚离开电场时刻的动能Ek和速度方向与水平方向夹角θ的正切值。
10.示波管是示波器的核心部分,它主要由电子枪、偏转系统和荧光屏三部分组成,如图甲所示.电子枪具有释放电子并使电子聚集成束以及加速的作用;偏转系统使电子束发生偏转;电子束打在荧光屏上形成光迹.这三部分均封装于真空玻璃壳中.已知电子的电荷量e=1.6×10C,质量m=0.91×10kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应.
(1)电子枪的三级加速可简化为如图乙所示的加速电场,若从阴极逸出电子的初速度可忽略不计,要使电子被加速后的动能达到16×10J,求加速电压为多大;
(2)电子被加速后进入偏转系统,若只考虑电子沿Y(竖直)方向的偏转情况,偏转系统可以简化为如图丙所示的偏转电场.偏转电极的极板长=4.0cm,两板间距离=1.0cm,极板右端与荧光屏的距离=18cm,当在偏转电极上加的正弦交变电压时,如果电子进入偏转电场的初速度m/s,求电子打在荧光屏上产生亮线的最大长度;
(3)如图甲所示,电子枪中灯丝用来加热阴极,使阴极发射电子.控制栅极的电势比阴极的电势低,调节阴极与控制栅极之间的电压,可控制通过栅极电子的数量.现要使打在荧光屏上电子的数量增加,应如何调节阴极与控制栅极之间的电压.电子枪中、和三个阳极除了对电子加速外,还共同完成对电子的聚焦作用,其中聚焦电场可简化为如图丁所示的电场,图中的虚线是该电场的等势线.请简要说明聚焦电场如何实现对电子的聚焦作用.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1) 2×104m/s;(2)①1.5×10-6kg;②1.09A
【解析】
【详解】
(1)根据
Ue=mv2
故获得的速度大小
v==2×104m/s
(2)①设每秒需要喷射△m的离子;则在时间t内喷射离子的质量为
m=△m×t
由牛顿第二定律可得
F=ma=m=△mv
所以
△m=kg=1.5×10-6kg
②因为
N=个=×1019个
故等效电流
I=≈1.09A
2.X偏转板带正电;Y偏转板带正电;原因见解析
【解析】
【详解】
电子受力方向与电场方向相反,因为电子打在荧光屏右上方,则可知电子向X偏转,电场方向为到,则X偏转板应带正电;同理可得,带正电。
3.(1);(2)见解析;(3)
【解析】
【详解】
(1)带电系统开始运动时,设加速度为a1,由牛顿第二定律
=
球B刚进入电场时,带电系统的速度为v1,有
求得
(2)对带电系统进行分析,假设球A能达到右极板,电场力对系统做功为W1,有
可见A还能穿过小孔,离开右极板。
假设球B能达到右极板,电场力对系统做功为W2,有
综上所述,带电系统速度第一次为零时,球A、B应分别在右极板两侧。
(3)假设球B能达到距右极x时,带电系统静止,由动能定理可得
解得
x=
4.(1);(2);(3)
【解析】
【详解】
(1)在电场中加速过程,由动能定理
得
根据
得离子的加速时间
离子在CD在之间匀速运动的时间
所以离子飞行的总时间
(2)若离子从C极板边缘飞出,此时离子做圆周运动的半径是最小的,其运动轨迹如图
由几何关系得
解得
因为
联立解得
离子比荷的取值范围。
(3)离子通过CD电场的时间
加速度
若时进入,偏转位移
刚好从极板下边缘飞出。
设离子在时刻进入,探测头接收到的时间
向下偏转位移大小
则探测头所处的坐标为
5.(1)
(2)
(3)
(4)(2-)L
【解析】
【详解】
试题分析:(1)M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上,所以圆心在C点,如图所示,设此时粒子运动轨迹半径为r1,CH=QC=L,即半径r1=L
由qUm=mv21
v1=
(2)又因为
得
(3)打在QE间的粒子在磁场中运动的时间最长,均为半个周期,
由 , ,得
(4)设粒子在磁场中运动的轨迹与CD板相切于K点,此轨迹的半径为r2,设圆心为A,在△AKC中:
解得r2=(-1)L,即KC=r2=( -1)L
所以CD板上可能被粒子打中的区域的长度s=HK,
即s=r1-r2=(2-)L(或 s=)
考点:带电粒子在匀强电场中及在匀强磁场中的运动
【名师点睛】本题考查带电粒子在匀强磁场中的运动,画出粒子的运动轨迹后,由几何关系求轨迹半径和圆心角是关键,要掌握住半径公式、周期公式;注意临界条件:当粒子的运动的轨迹恰好与CD板相切时,这是粒子能达到的最下边的边缘.
6.(1) (2) (3)
【解析】
【详解】
(1) 在内,电场力为:
根据牛顿二定律:,则
在内,电场力为:
根据牛顿第二定律:,所以
由此可画出a-t图如下图所示:
小球在A、B板间水平方向运动为匀速运动,则时间
所以竖直方向:,方向竖直向上;
(2)小球在板间运动的过程中,由动量定理:
所以;
(3)由a-t图,当小球从0秒时射入,离开A、B板的竖直速度正向最大,为
当小球从0.1s时射入,离开A、B板的竖直速度负向最大,为
所以小球可以在任意时刻、从A、B板左侧任意位置进入板间,
所以可以找到合适位置、合适时刻,使小球恰好从A板最右侧飞出时,竖直速度正向最大,为;使小球恰好从B板最右侧飞出时,竖直速度负向最大,为
又因为小球飞出A、B板间后做匀速直线运动,经历时间
所以小球打在挡板上的长度范围:
点睛:能根据根据牛顿第二定律,求出加速度与时间的关系图像,然后根据运动学规律求解,同时要掌握类平抛运动物体的处理方法是解决本题的关键.
7.(1) ,负电;(2)
【解析】
【详解】
(1)粒子在电场中做直线运动,对其受力分析如图所示,受到竖直向下的重力和水平向左的电场力,所受电场力与电场方向相反,故带电粒子带负电
(2)根据力的合成定则可得
得
8.(1)3m/s2;(2);(3)-360V
【解析】
【详解】
(1)根据几何关系得斜面的长度为
根据运动学公式有
解得
(2)由牛顿第二定律得
解得
(3)电场中a到b两点之间的电势差
9.(1);(2);(3),
【解析】
【分析】
【详解】
(1)由动能定理可得
解得
(2)粒子在偏转电场中运动的时间为
偏转量为
(3)离开时竖直方向的速度为
故离开时的动能为
速度方向与水平方向夹角θ的正切值
10.(1)1.0×103V(2)10cm(3)要使打在荧光屏上电子数目增加,应将阴极与控制栅极之间的电压调低
【解析】
【详解】
解:(1)对于电子通过加速电场的过程,根据动能定理有:
代入数据解得:V
(2)由V,可知角速度为rad/s
则偏转电场变化的周期为:s
而,因为
可见每个电子通过偏转电场的过程中,电场可视为稳定的匀强电场
设偏转电场电压为时,电子刚好飞出偏转电场,此时电子沿电场方向的位移为
根据牛顿第二定律和运动学公式有:
解得:V
所以为使电子能打在荧光屏上,所加偏转电压应小于320V
当加在偏转电极上的偏转电压为V时,且电子刚好飞出偏转电场,电子沿电场方向的最大位移恰为
设电子射出偏转电场的速度与初速度方向的最大夹角为,则有:
电子打在荧光屏上的最大偏移量:cm
由对称性可得电子打在荧光屏产生亮线的最大长度为cm
(3)现要使打在荧光屏上电子数目增加,应将阴极与控制栅极之间的电压调低,聚焦电场如图所示:
由力和运动的关系可知:电子在沿示波管中心轴线所受电场力与电子沿此方向速度相反,电子沿示波管中心轴线方向做减速运动;电子在垂直波管中民主轴线方向,受电场力指向中心轴线,在此方向电子做加速运动.由对称性可知电子束有向着中心会聚的特点,适当调节电场可以使电子速聚焦在中心,轴线上一点,因此这样的电场分布将对射入的发散的电子束有会聚作用.
答案第1页,共2页
答案第1页,共2页
一、解答题
1.宇宙飞船进行长距离星际运行时,不能再用化学燃料,可采用一种新型发动机——离子发动机,小型高效的离子发动机所用燃料不到化学燃料发动机的,它可以使太空中的航天器获得动力,进而调整航天器的飞行姿态或飞行轨道。在离子发动机中,由电极发射的电子射入稀有气体(如氙气),使其离子化,然后从静止开始经电场加速后,从飞船尾部高速连续喷出,利用反冲使飞船本身得到加速。已知氙离子质量为m=2.2×10-25kg,电荷e=1.6×10-19C,加速电压U=275V。
(1)氙离子经电场加速后,获得的速度大小。
(2)为了使飞船得到F=3.0×10-2N的反冲力,求:
①每秒需要喷射出多少质量的氙离子;
②飞船向后喷出的氙离子形成的等效电流I。
2.在如图所示的示波管中,如果在荧光屏右上方出现亮斑,那么示波管中的X偏转板应带什么电?Y偏转板应带什么电?为什么?
3.如图所示,沿水平方向放置一条平直光滑槽,它垂直穿过开有小孔的两平行薄板,板相距3.5L。槽内有两个质量均为m的小球A和B,球A带电量为+2q,球B带电量为-3q,两球由长为2L的轻杆相连,组成一带电系统。最初A和B分别静止于左板的两侧,离板的距离均为L。若视小球为质点,不计轻杆的质量,在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成,不影响电场的分布),求:
(1)球B刚进入电场时,带电系统的速度大小;
(2)带电系统的A球是否能到达右板,说明理由?
(3)带电系统从开始运动到速度第一次为零时球B相对右板的位置?
4.飞行时间质谱仪通过探测不同离子到达探测头时间,可以测得离子比荷。如图甲所示,探测头在探测器左端中点。脉冲阀P喷出微量气体,经激光S照射产生不同价位的离子,假设正离子在A极板处初速度为零,AB极板间的加速电压为U0,离子加速后从B板小孔射出,沿中心线方向进入C、D板间的偏转控制区。已知加速电场AB间距为d,偏转极板CD的长度及宽度均为L。设加速电场和偏转电场均为匀强电场,不计离子重力和离子间相互作用。
(1)若偏转电压UCD=0,某比荷为k的离子沿中心线到达探测头,求该离子飞行总时间;
(2)若偏转电压UCD=0,在C、D板间加上垂直于纸面向里的匀强磁场,磁感应强度为B,要使所有离子均能通过控制区域并从右侧飞出,求这些离子比荷的取值范围;
(3)若偏转电压UCD与时间t的关系如图乙所示,最大值Um=4U0,周期,假设离子比荷为k,并且在t=0时刻开始连续均匀地射入偏转电场。以D极板的右端点为坐标原点,竖直向上为y轴正方向,探测头可在y轴上自由移动,在t=T到时间内,要使探测头能收集到所有粒子,求探测头坐标y随时间t变化的关系。
5.如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到最大值Um之间的各种数值.静止的带电粒子电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁场方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ= 45°,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上.求:
(1)当M、N两板间电压取最大值Um时,粒子射入磁场的速度v1的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)粒子在磁场中运动的最长时间tm;
(4)CD板上可能被粒子打中区域的长度S.
6.如图甲所示,两水平放置的平行金属板A、B间距d=40cm,板长L=30cm,在两板间加一大小和方向随之间周期性变化的匀强电场,如图乙所示,规定竖直向上为电场强度的正方向.在距金属板右侧D=40cm的空间内有方向竖直向上、电场强度大小为E=100V/m的匀强磁场,并在该电场的右侧边界竖直放置一足够长的挡板.现有一电量q=1×10-2C、质量m=0.1kg的正电小球在t=0时刻以水平初速度v0=2m/s从距B板h=5cm处射入A、B两板间,重力加速度g=10m/s2,求:
(1)小球飞出A、B两板间时竖直方向的速度的大小;
(2)小球在A、B极板间运动过程中受到电场力的平均值;
(3)若有大量电量为q=10-2C、质量m=0.1kg的正电小球持续不断地从极板左侧各个位置以相同水平初速度v0水平进入A、B板间,忽略小球间的相互作用,求这些小球最终打在挡板上的长度范围.
7.如图所示,竖直面内分布有水平向右的匀强电场,一带电粒子的质量为,带电量为,该粒子沿图中虚线从运动到,虚线与水平方向的夹角为,重力加速度为.求:
(1)画出带电粒子的受力分析图,并判断带电粒子的电性;
(2)匀强电场的电场强度的大小。
8.如图所示,倾角的光滑斜面固定在水平地面上,斜面顶端a离地高度,整个装置处于水平向左的匀强电场中,一个质量,带电量的物体(可视为质点)从斜面顶端静止释放,经过到达斜面底端b点(g取)。求:
(1)物体沿斜面下滑的加速度大小;
(2)电场强度E的大小(结果带根号);
(3)电场中a到b两点之间的电势差。
9.带电量为q,质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器,进入时速度和电容器中的场强方向垂直。已知:电容器的极板长为L,极板间距为d,两极板的电压为U2,重力不计,求:
(1)经过加速电场后的速度v0;
(2)离开电容器电场时的偏转量y;
(3)刚离开电场时刻的动能Ek和速度方向与水平方向夹角θ的正切值。
10.示波管是示波器的核心部分,它主要由电子枪、偏转系统和荧光屏三部分组成,如图甲所示.电子枪具有释放电子并使电子聚集成束以及加速的作用;偏转系统使电子束发生偏转;电子束打在荧光屏上形成光迹.这三部分均封装于真空玻璃壳中.已知电子的电荷量e=1.6×10C,质量m=0.91×10kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应.
(1)电子枪的三级加速可简化为如图乙所示的加速电场,若从阴极逸出电子的初速度可忽略不计,要使电子被加速后的动能达到16×10J,求加速电压为多大;
(2)电子被加速后进入偏转系统,若只考虑电子沿Y(竖直)方向的偏转情况,偏转系统可以简化为如图丙所示的偏转电场.偏转电极的极板长=4.0cm,两板间距离=1.0cm,极板右端与荧光屏的距离=18cm,当在偏转电极上加的正弦交变电压时,如果电子进入偏转电场的初速度m/s,求电子打在荧光屏上产生亮线的最大长度;
(3)如图甲所示,电子枪中灯丝用来加热阴极,使阴极发射电子.控制栅极的电势比阴极的电势低,调节阴极与控制栅极之间的电压,可控制通过栅极电子的数量.现要使打在荧光屏上电子的数量增加,应如何调节阴极与控制栅极之间的电压.电子枪中、和三个阳极除了对电子加速外,还共同完成对电子的聚焦作用,其中聚焦电场可简化为如图丁所示的电场,图中的虚线是该电场的等势线.请简要说明聚焦电场如何实现对电子的聚焦作用.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1) 2×104m/s;(2)①1.5×10-6kg;②1.09A
【解析】
【详解】
(1)根据
Ue=mv2
故获得的速度大小
v==2×104m/s
(2)①设每秒需要喷射△m的离子;则在时间t内喷射离子的质量为
m=△m×t
由牛顿第二定律可得
F=ma=m=△mv
所以
△m=kg=1.5×10-6kg
②因为
N=个=×1019个
故等效电流
I=≈1.09A
2.X偏转板带正电;Y偏转板带正电;原因见解析
【解析】
【详解】
电子受力方向与电场方向相反,因为电子打在荧光屏右上方,则可知电子向X偏转,电场方向为到,则X偏转板应带正电;同理可得,带正电。
3.(1);(2)见解析;(3)
【解析】
【详解】
(1)带电系统开始运动时,设加速度为a1,由牛顿第二定律
=
球B刚进入电场时,带电系统的速度为v1,有
求得
(2)对带电系统进行分析,假设球A能达到右极板,电场力对系统做功为W1,有
可见A还能穿过小孔,离开右极板。
假设球B能达到右极板,电场力对系统做功为W2,有
综上所述,带电系统速度第一次为零时,球A、B应分别在右极板两侧。
(3)假设球B能达到距右极x时,带电系统静止,由动能定理可得
解得
x=
4.(1);(2);(3)
【解析】
【详解】
(1)在电场中加速过程,由动能定理
得
根据
得离子的加速时间
离子在CD在之间匀速运动的时间
所以离子飞行的总时间
(2)若离子从C极板边缘飞出,此时离子做圆周运动的半径是最小的,其运动轨迹如图
由几何关系得
解得
因为
联立解得
离子比荷的取值范围。
(3)离子通过CD电场的时间
加速度
若时进入,偏转位移
刚好从极板下边缘飞出。
设离子在时刻进入,探测头接收到的时间
向下偏转位移大小
则探测头所处的坐标为
5.(1)
(2)
(3)
(4)(2-)L
【解析】
【详解】
试题分析:(1)M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上,所以圆心在C点,如图所示,设此时粒子运动轨迹半径为r1,CH=QC=L,即半径r1=L
由qUm=mv21
v1=
(2)又因为
得
(3)打在QE间的粒子在磁场中运动的时间最长,均为半个周期,
由 , ,得
(4)设粒子在磁场中运动的轨迹与CD板相切于K点,此轨迹的半径为r2,设圆心为A,在△AKC中:
解得r2=(-1)L,即KC=r2=( -1)L
所以CD板上可能被粒子打中的区域的长度s=HK,
即s=r1-r2=(2-)L(或 s=)
考点:带电粒子在匀强电场中及在匀强磁场中的运动
【名师点睛】本题考查带电粒子在匀强磁场中的运动,画出粒子的运动轨迹后,由几何关系求轨迹半径和圆心角是关键,要掌握住半径公式、周期公式;注意临界条件:当粒子的运动的轨迹恰好与CD板相切时,这是粒子能达到的最下边的边缘.
6.(1) (2) (3)
【解析】
【详解】
(1) 在内,电场力为:
根据牛顿二定律:,则
在内,电场力为:
根据牛顿第二定律:,所以
由此可画出a-t图如下图所示:
小球在A、B板间水平方向运动为匀速运动,则时间
所以竖直方向:,方向竖直向上;
(2)小球在板间运动的过程中,由动量定理:
所以;
(3)由a-t图,当小球从0秒时射入,离开A、B板的竖直速度正向最大,为
当小球从0.1s时射入,离开A、B板的竖直速度负向最大,为
所以小球可以在任意时刻、从A、B板左侧任意位置进入板间,
所以可以找到合适位置、合适时刻,使小球恰好从A板最右侧飞出时,竖直速度正向最大,为;使小球恰好从B板最右侧飞出时,竖直速度负向最大,为
又因为小球飞出A、B板间后做匀速直线运动,经历时间
所以小球打在挡板上的长度范围:
点睛:能根据根据牛顿第二定律,求出加速度与时间的关系图像,然后根据运动学规律求解,同时要掌握类平抛运动物体的处理方法是解决本题的关键.
7.(1) ,负电;(2)
【解析】
【详解】
(1)粒子在电场中做直线运动,对其受力分析如图所示,受到竖直向下的重力和水平向左的电场力,所受电场力与电场方向相反,故带电粒子带负电
(2)根据力的合成定则可得
得
8.(1)3m/s2;(2);(3)-360V
【解析】
【详解】
(1)根据几何关系得斜面的长度为
根据运动学公式有
解得
(2)由牛顿第二定律得
解得
(3)电场中a到b两点之间的电势差
9.(1);(2);(3),
【解析】
【分析】
【详解】
(1)由动能定理可得
解得
(2)粒子在偏转电场中运动的时间为
偏转量为
(3)离开时竖直方向的速度为
故离开时的动能为
速度方向与水平方向夹角θ的正切值
10.(1)1.0×103V(2)10cm(3)要使打在荧光屏上电子数目增加,应将阴极与控制栅极之间的电压调低
【解析】
【详解】
解:(1)对于电子通过加速电场的过程,根据动能定理有:
代入数据解得:V
(2)由V,可知角速度为rad/s
则偏转电场变化的周期为:s
而,因为
可见每个电子通过偏转电场的过程中,电场可视为稳定的匀强电场
设偏转电场电压为时,电子刚好飞出偏转电场,此时电子沿电场方向的位移为
根据牛顿第二定律和运动学公式有:
解得:V
所以为使电子能打在荧光屏上,所加偏转电压应小于320V
当加在偏转电极上的偏转电压为V时,且电子刚好飞出偏转电场,电子沿电场方向的最大位移恰为
设电子射出偏转电场的速度与初速度方向的最大夹角为,则有:
电子打在荧光屏上的最大偏移量:cm
由对称性可得电子打在荧光屏产生亮线的最大长度为cm
(3)现要使打在荧光屏上电子数目增加,应将阴极与控制栅极之间的电压调低,聚焦电场如图所示:
由力和运动的关系可知:电子在沿示波管中心轴线所受电场力与电子沿此方向速度相反,电子沿示波管中心轴线方向做减速运动;电子在垂直波管中民主轴线方向,受电场力指向中心轴线,在此方向电子做加速运动.由对称性可知电子束有向着中心会聚的特点,适当调节电场可以使电子速聚焦在中心,轴线上一点,因此这样的电场分布将对射入的发散的电子束有会聚作用.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 静电场的描述
- 第一节 静电现象
- 第二节 库仑定律
- 第三节 电场 电场强度
- 第四节 电势能与电势
- 第五节 电势差及其与电场强度的关系
- 第二章 静电场的应用
- 第一节 电容器与电容
- 第二节 带电粒子在电场中的运动
- 第三节 静电的利用与防护
- 第三章 恒定电流
- 第一节 导体的伏安特性曲线
- 第二节 决定导体电阻大小的因素
- 第三节 测量金属丝的电阻率
- 第四节 电阻的串联和并联
- 第四章 闭合电路
- 第一节 常见的电路元器件
- 第二节 闭合电路的欧姆定律
- 第三节 测量电源的电动势和内阻
- 第四节 练习使用多用电表
- 第五节 家庭电路与安全用电
- 第五章 电能与能源的可持续发展
- 第一节 电路中的能量
- 第二节 能源的利用方式
- 第三节 能量的转化与守恒
- 第四节 能源与环境
- 第六章 电磁现象与电磁波
- 第一节 磁现象与磁场
- 第二节 磁感应强度
- 第三节 电磁感应现象
- 第四节 电磁波及其应用
- 第五节 量子化现象
