5.2运动的合成与分解学案(word附答案)
文档属性
| 名称 | 5.2运动的合成与分解学案(word附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 781.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览



文档简介
第2节 运动的合成与分解
学习目标
1.经历蜡块运动的探究过程,体会研究曲线运动的方法——运动的合成与分解。
2.理解合运动、分运动的概念,掌握运动的合成与分解的方法。
3.通过对合运动和分运动的分析,体会等效替代的思想在物理学中的应用。
4.能运用合成与分解的思想分析两类典型的运动模型——“小船渡河”模型和“关联速度”模型。
自主预习
一、蜡块的运动
1.
蜡块的位置:如图所示,蜡块沿玻璃管匀速上升的速度设为vy,玻璃管向右匀速移动的速度设为vx,从蜡块开始运动的时刻开始计时,在某时刻t,蜡块的位置P可以用它的x、y两个坐标表示:x= ,y= 。
2.蜡块运动的速度:大小v= ,方向满足tan θ= 。
3.蜡块运动的轨迹: ,是一条过原点的直线。
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体 就是合运动, 就是分运动。
2.运动的合成与分解:已知分运动求合运动的过程,叫 ;已知合运动求分运动的过程,叫 。
3.运动的合成与分解实质是对运动的位移、速度和加速度的合成和分解,遵循矢量运算法则。
课堂探究
一、蜡块的运动
[情境设问]观察蜡块的运动微视频,蜡块运动的轨迹是怎样的 蜡块的速度是怎样的
二、运动的合成与分解
[情境设问]蜡块在水平方向是什么运动 在竖直方向做什么运动 实际上做的是什么运动
[思考与讨论]同学们观察一下蜡块的运动:
1.水平、竖直方向的运动与实际的运动是同时进行的吗
2.水平、竖直方向的运动与实际的运动产生的效果一样吗
3.水平、竖直方向的运动与实际的运动是发生在同一个物体上吗
4.水平、竖直方向的运动与实际的运动可以分开研究吗
总结:合运动与分运动具有的特性: , , , 。
三、小船渡河问题的研究
[情境设问]观看小船渡河平面图,思考小船渡河过程中参与了哪两个运动 合运动是什么性质的运动
[思考与讨论]请同学们思考一下如何求解最短的渡河时间
[思考与讨论]最短的渡河位移是多少呢
1.当v船>v水时:
2.当v船四、关联速度问题
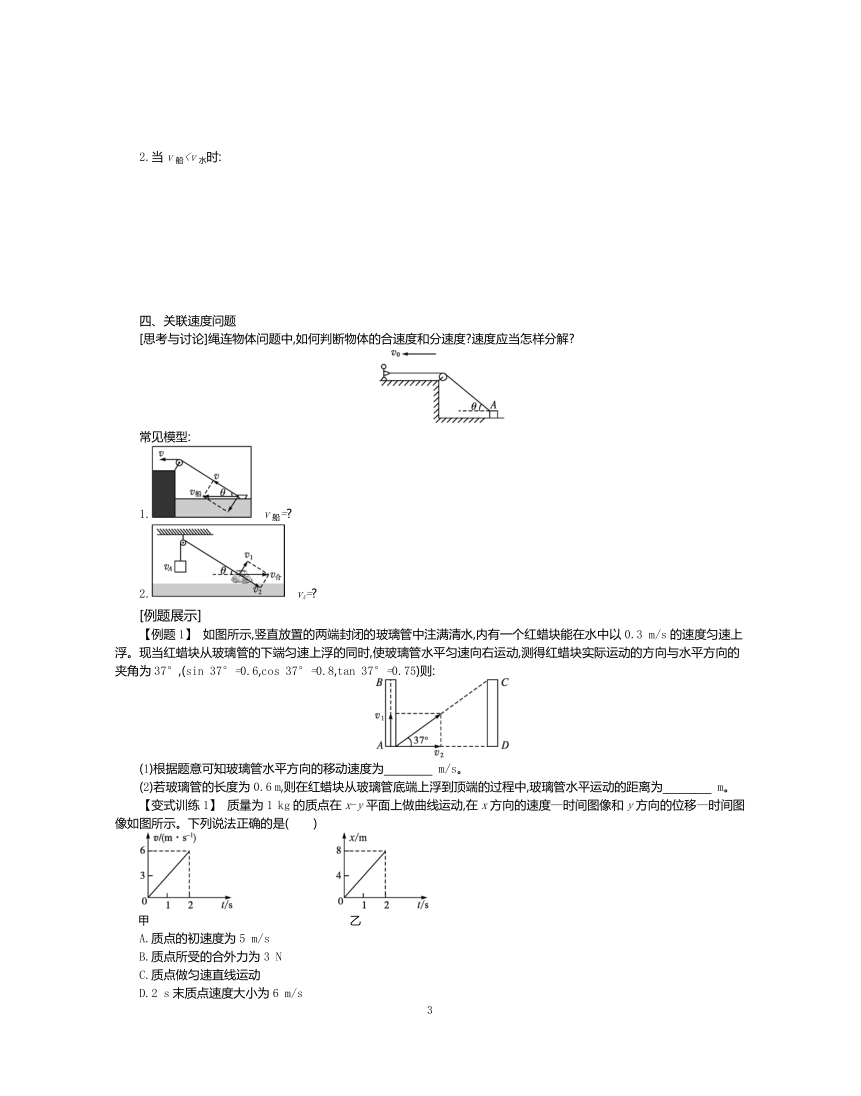
[思考与讨论]绳连物体问题中,如何判断物体的合速度和分速度 速度应当怎样分解
常见模型:
1. v船=
2. vA=
[例题展示]
【例题1】 如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.3 m/s的速度匀速上浮。现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,(sin 37°=0.6,cos 37°=0.8,tan 37°=0.75)则:
(1)根据题意可知玻璃管水平方向的移动速度为 m/s。
(2)若玻璃管的长度为0.6 m,则在红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平运动的距离为 m。
【变式训练1】 质量为1 kg的质点在x-y平面上做曲线运动,在x方向的速度—时间图像和y方向的位移—时间图像如图所示。下列说法正确的是( )
甲 乙
A.质点的初速度为5 m/s
B.质点所受的合外力为3 N
C.质点做匀速直线运动
D.2 s末质点速度大小为6 m/s
【例题2】 一小船渡河,河宽d=180 m,水流速度为v1=3 m/s,船在静水中的速度为v2=4 m/s,求:(1)小船渡河的最短时间为多少 此时渡河位移是多大
(2)欲使船渡河的航程最短,船头应朝什么方向 用多长时间
【变式训练2】 某人划船横渡一条河流,已知船在静水中的速率恒为v1,水流速率恒为v2,且v1>v2。他以最短时间方式过河用时T1,以最短位移方式过河用时T2。则T1与T2的比值为( )
A. B.
C. D.
【例题3】 如图所示,以速度v沿竖直杆匀速下滑的物体A用轻绳通过定滑轮拉物体B,当绳与水平面夹角是θ时,物体B的速度为多少
【变式训练3】
如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v0,小船水平向左运动,小船与滑轮间的绳某时刻与水平方向夹角为α,则小船的运动性质及此时刻小船的速度v船为( )
A.小船做加速运动,v船=
B.小船做加速运动,v船=v0cos α
C.小船做匀速直线运动,v船=
D.小船做匀速直线运动,v船=v0cos α
[课堂练习]
1.为了抗击疫情,保障百姓基本生活,许多快递公司推出了“无接触配送”。快递小哥想到了用无人机配送快递的方法。某次配送快递无人机在飞行过程中,水平方向速度vx及竖直方向速度vy与飞行时间t的关系图像如图甲、图乙所示。关于无人机运动说法正确的是( )
甲 乙
A.0~t1时间内,无人机做曲线运动
B.t2时刻,无人机运动到最高点
C.t3~t4时间内,无人机做匀变速直线运动
D.t2时刻,无人机的速度为
2.一艘小船在静水中的速度为3 m/s,渡过一条宽150 m,水流速度为4 m/s的河流,则该小船( )
A.能到达正对岸
B.渡河的时间可能少于50 s
C.以最短位移渡河时,位移大小为200 m
D.以最短时间渡河时,沿水流方向的位移大小为240 m
3.如图所示,小车m以速度v沿斜面匀速向下运动,并通过绳子带动重物M沿竖直杆上滑。则当滑轮右侧的绳子与竖直方向成θ角时,重物M上滑的速度为( )
A.vsin θ B.vcos θ C.vtan θ D.
核心素养专练
1.关于运动的合成和分解,下列说法正确的是( )
A.运动的合速度一定大于两个分运动的速度
B.运动的合速度一定大于其中一个分运动的速度
C.运动的合速度方向就是物体实际运动的方向
D.知道两个分速度的大小就可以确定合速度的大小
2.河宽420 m,船在静水中速度为4 m/s,水流速度是3 m/s,则船过河的最短时间为( )
A.140 s B.105 s C.84 s D.60 s
3.小船过河时,船头偏向上游与水流方向成α角,船相对静水的速度为v,其航线恰好垂直于河岸。现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是( )
A.增大α角,增大船速v
B.减小α角,增大船速v
C.减小α角,保持船速v不变
D.增大α角,保持船速v不变
4.如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下面说法正确的是( )
A.物体做匀速运动,且v1=v2
B.物体做加速运动,且v2>v1
C.物体做加速运动,且FT>G
D.物体做匀速运动,且FT=G
5.(多选)有a、b两个分运动,它们的合运动为c,则下列说法正确的是( )
A.若a、b的轨迹为直线,则c的轨迹必为直线
B.若c的轨迹为直线,则a、b必为匀速运动
C.若a为匀速直线运动,b为匀速直线运动,则c必为匀速直线运动
D.若a、b均为初速度为零的匀变速直线运动,则c必为匀变速直线运动
6.
表演“顶竿”杂技时,站在地上的演员扛一竹竿,演员和竹竿的总质量为80 kg,一质量为10 kg的小猴(可当质点处理)在竿底端从静止开始以2 m/s2加速上爬,同时演员以1 m/s 的速度水平向右匀速移动,以猴的出发点为坐标原点,建立平面直角坐标系如图所示,g取10 m/s2。
(1)求2 s时猴子的位置(用坐标表示);
(2)2 s时猴子的瞬时速度为多大
(3)求在此过程中,演员对地面的压力的大小。(根号可保留)
7.一条两岸平行的河流宽为30 m,水速v1=10 m/s,一只小船想到对岸,但在船出发点下游30 m处有瀑布。为使小船安全地行驶到对岸而不从瀑布掉下,则此时船相对于水的v2至少为多大 船头指向何处
第2节 运动的合成与分解
参考答案
自主预习
一、蜡块的运动
1.vxt vyt
2.
3.y=x
二、运动的合成与分解
1.实际发生的运动 参与的几个运动
2.运动的合成 运动的分解
课堂探究
一、[情境设问]蜡块做倾斜向上的直线运动,蜡块的速度是由水平速度和竖直速度根据勾股定理求得的,方向沿着蜡块实际运动的方向。
二、[情境设问]蜡块在水平方向做匀速直线运动,在竖直方向向上做匀速直线运动,实际上也做了匀速直线运动。
[思考与讨论]等时性 等效性 同体性 独立性
三、[情境设问]小船参与了垂直河岸方向的匀速直线运动和沿着河岸方向的匀速直线运动,合运动也是沿着合速度方向的匀速直线运动。
[思考与讨论]t==,当θ最大等于90°时,sin 90°=1,此时时间t最短。所以当船头垂直于河岸渡河时,渡河时间最短,tmin=。
[思考与讨论]1.当v船>v水时,渡河的最短位移是河宽d。
2.当v船四、[思考与讨论]物体的合速度是物体实际运动的速度,应将合速度沿着绳和垂直于绳方向进行分解。
常见模型:v船= vA=v合cos θ
【例题1】 根据tan 37°=解得v2=0.4 m/s。根据y=v1t解得t=2 s。又因为x=v2t可得x=0.8 m。
【变式训练1】 B
【例题2】 (1)tmin==45 s。合速度v=5 m/s。l=vtmin=225 m。
(2)最短航程等于河宽d。cos θ==0.75。根据勾股定理可以求得合速度
v= m/s,t== s。
【变式训练2】 D
【例题3】 vB=vsin θ
【变式训练3】 A
课堂练习
1.D 2.C 3.D
核心素养专练
1.C 2.B 3.A 4.C 5.CD
6.(1)(2 m,4 m) (2) m/s (3)920 N
7.5 m/s 船头指向与上游河岸的夹角为60°
1
学习目标
1.经历蜡块运动的探究过程,体会研究曲线运动的方法——运动的合成与分解。
2.理解合运动、分运动的概念,掌握运动的合成与分解的方法。
3.通过对合运动和分运动的分析,体会等效替代的思想在物理学中的应用。
4.能运用合成与分解的思想分析两类典型的运动模型——“小船渡河”模型和“关联速度”模型。
自主预习
一、蜡块的运动
1.
蜡块的位置:如图所示,蜡块沿玻璃管匀速上升的速度设为vy,玻璃管向右匀速移动的速度设为vx,从蜡块开始运动的时刻开始计时,在某时刻t,蜡块的位置P可以用它的x、y两个坐标表示:x= ,y= 。
2.蜡块运动的速度:大小v= ,方向满足tan θ= 。
3.蜡块运动的轨迹: ,是一条过原点的直线。
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体 就是合运动, 就是分运动。
2.运动的合成与分解:已知分运动求合运动的过程,叫 ;已知合运动求分运动的过程,叫 。
3.运动的合成与分解实质是对运动的位移、速度和加速度的合成和分解,遵循矢量运算法则。
课堂探究
一、蜡块的运动
[情境设问]观察蜡块的运动微视频,蜡块运动的轨迹是怎样的 蜡块的速度是怎样的
二、运动的合成与分解
[情境设问]蜡块在水平方向是什么运动 在竖直方向做什么运动 实际上做的是什么运动
[思考与讨论]同学们观察一下蜡块的运动:
1.水平、竖直方向的运动与实际的运动是同时进行的吗
2.水平、竖直方向的运动与实际的运动产生的效果一样吗
3.水平、竖直方向的运动与实际的运动是发生在同一个物体上吗
4.水平、竖直方向的运动与实际的运动可以分开研究吗
总结:合运动与分运动具有的特性: , , , 。
三、小船渡河问题的研究
[情境设问]观看小船渡河平面图,思考小船渡河过程中参与了哪两个运动 合运动是什么性质的运动
[思考与讨论]请同学们思考一下如何求解最短的渡河时间
[思考与讨论]最短的渡河位移是多少呢
1.当v船>v水时:
2.当v船
[思考与讨论]绳连物体问题中,如何判断物体的合速度和分速度 速度应当怎样分解
常见模型:
1. v船=
2. vA=
[例题展示]
【例题1】 如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.3 m/s的速度匀速上浮。现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,(sin 37°=0.6,cos 37°=0.8,tan 37°=0.75)则:
(1)根据题意可知玻璃管水平方向的移动速度为 m/s。
(2)若玻璃管的长度为0.6 m,则在红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平运动的距离为 m。
【变式训练1】 质量为1 kg的质点在x-y平面上做曲线运动,在x方向的速度—时间图像和y方向的位移—时间图像如图所示。下列说法正确的是( )
甲 乙
A.质点的初速度为5 m/s
B.质点所受的合外力为3 N
C.质点做匀速直线运动
D.2 s末质点速度大小为6 m/s
【例题2】 一小船渡河,河宽d=180 m,水流速度为v1=3 m/s,船在静水中的速度为v2=4 m/s,求:(1)小船渡河的最短时间为多少 此时渡河位移是多大
(2)欲使船渡河的航程最短,船头应朝什么方向 用多长时间
【变式训练2】 某人划船横渡一条河流,已知船在静水中的速率恒为v1,水流速率恒为v2,且v1>v2。他以最短时间方式过河用时T1,以最短位移方式过河用时T2。则T1与T2的比值为( )
A. B.
C. D.
【例题3】 如图所示,以速度v沿竖直杆匀速下滑的物体A用轻绳通过定滑轮拉物体B,当绳与水平面夹角是θ时,物体B的速度为多少
【变式训练3】
如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳的速度为v0,小船水平向左运动,小船与滑轮间的绳某时刻与水平方向夹角为α,则小船的运动性质及此时刻小船的速度v船为( )
A.小船做加速运动,v船=
B.小船做加速运动,v船=v0cos α
C.小船做匀速直线运动,v船=
D.小船做匀速直线运动,v船=v0cos α
[课堂练习]
1.为了抗击疫情,保障百姓基本生活,许多快递公司推出了“无接触配送”。快递小哥想到了用无人机配送快递的方法。某次配送快递无人机在飞行过程中,水平方向速度vx及竖直方向速度vy与飞行时间t的关系图像如图甲、图乙所示。关于无人机运动说法正确的是( )
甲 乙
A.0~t1时间内,无人机做曲线运动
B.t2时刻,无人机运动到最高点
C.t3~t4时间内,无人机做匀变速直线运动
D.t2时刻,无人机的速度为
2.一艘小船在静水中的速度为3 m/s,渡过一条宽150 m,水流速度为4 m/s的河流,则该小船( )
A.能到达正对岸
B.渡河的时间可能少于50 s
C.以最短位移渡河时,位移大小为200 m
D.以最短时间渡河时,沿水流方向的位移大小为240 m
3.如图所示,小车m以速度v沿斜面匀速向下运动,并通过绳子带动重物M沿竖直杆上滑。则当滑轮右侧的绳子与竖直方向成θ角时,重物M上滑的速度为( )
A.vsin θ B.vcos θ C.vtan θ D.
核心素养专练
1.关于运动的合成和分解,下列说法正确的是( )
A.运动的合速度一定大于两个分运动的速度
B.运动的合速度一定大于其中一个分运动的速度
C.运动的合速度方向就是物体实际运动的方向
D.知道两个分速度的大小就可以确定合速度的大小
2.河宽420 m,船在静水中速度为4 m/s,水流速度是3 m/s,则船过河的最短时间为( )
A.140 s B.105 s C.84 s D.60 s
3.小船过河时,船头偏向上游与水流方向成α角,船相对静水的速度为v,其航线恰好垂直于河岸。现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是( )
A.增大α角,增大船速v
B.减小α角,增大船速v
C.减小α角,保持船速v不变
D.增大α角,保持船速v不变
4.如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下面说法正确的是( )
A.物体做匀速运动,且v1=v2
B.物体做加速运动,且v2>v1
C.物体做加速运动,且FT>G
D.物体做匀速运动,且FT=G
5.(多选)有a、b两个分运动,它们的合运动为c,则下列说法正确的是( )
A.若a、b的轨迹为直线,则c的轨迹必为直线
B.若c的轨迹为直线,则a、b必为匀速运动
C.若a为匀速直线运动,b为匀速直线运动,则c必为匀速直线运动
D.若a、b均为初速度为零的匀变速直线运动,则c必为匀变速直线运动
6.
表演“顶竿”杂技时,站在地上的演员扛一竹竿,演员和竹竿的总质量为80 kg,一质量为10 kg的小猴(可当质点处理)在竿底端从静止开始以2 m/s2加速上爬,同时演员以1 m/s 的速度水平向右匀速移动,以猴的出发点为坐标原点,建立平面直角坐标系如图所示,g取10 m/s2。
(1)求2 s时猴子的位置(用坐标表示);
(2)2 s时猴子的瞬时速度为多大
(3)求在此过程中,演员对地面的压力的大小。(根号可保留)
7.一条两岸平行的河流宽为30 m,水速v1=10 m/s,一只小船想到对岸,但在船出发点下游30 m处有瀑布。为使小船安全地行驶到对岸而不从瀑布掉下,则此时船相对于水的v2至少为多大 船头指向何处
第2节 运动的合成与分解
参考答案
自主预习
一、蜡块的运动
1.vxt vyt
2.
3.y=x
二、运动的合成与分解
1.实际发生的运动 参与的几个运动
2.运动的合成 运动的分解
课堂探究
一、[情境设问]蜡块做倾斜向上的直线运动,蜡块的速度是由水平速度和竖直速度根据勾股定理求得的,方向沿着蜡块实际运动的方向。
二、[情境设问]蜡块在水平方向做匀速直线运动,在竖直方向向上做匀速直线运动,实际上也做了匀速直线运动。
[思考与讨论]等时性 等效性 同体性 独立性
三、[情境设问]小船参与了垂直河岸方向的匀速直线运动和沿着河岸方向的匀速直线运动,合运动也是沿着合速度方向的匀速直线运动。
[思考与讨论]t==,当θ最大等于90°时,sin 90°=1,此时时间t最短。所以当船头垂直于河岸渡河时,渡河时间最短,tmin=。
[思考与讨论]1.当v船>v水时,渡河的最短位移是河宽d。
2.当v船
常见模型:v船= vA=v合cos θ
【例题1】 根据tan 37°=解得v2=0.4 m/s。根据y=v1t解得t=2 s。又因为x=v2t可得x=0.8 m。
【变式训练1】 B
【例题2】 (1)tmin==45 s。合速度v=5 m/s。l=vtmin=225 m。
(2)最短航程等于河宽d。cos θ==0.75。根据勾股定理可以求得合速度
v= m/s,t== s。
【变式训练2】 D
【例题3】 vB=vsin θ
【变式训练3】 A
课堂练习
1.D 2.C 3.D
核心素养专练
1.C 2.B 3.A 4.C 5.CD
6.(1)(2 m,4 m) (2) m/s (3)920 N
7.5 m/s 船头指向与上游河岸的夹角为60°
1
