华东师大版八年级下册数学18.2 平行四边形的判定 课件(共20张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学18.2 平行四边形的判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 233.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 21:27:40 | ||
图片预览








文档简介
(共20张PPT)
18.2 平行四边形的判定
Contents
目录
02
03
04
学习目标
新知探究
随堂练习
05
课堂小结
01
旧知回顾
边
对边平行
对边相等
角
对角相等
邻角互补
对角线
对角线互相平分
2、平行四边形的性质
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形。
平行四边形的性质
1.理解并掌握平行四边形的判定方法(定义法、判定定理一、定理二);
2.能运用这三种方法来证明一个四边形是平行四边形.
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
根据定义是一种最基本、最重要的判定方法。
思考
平行四边形的两组对边分别相等
你能说出它的逆命题吗?
两组对边分别相等的四边形是平行四边形。
它是一个真命题吗?
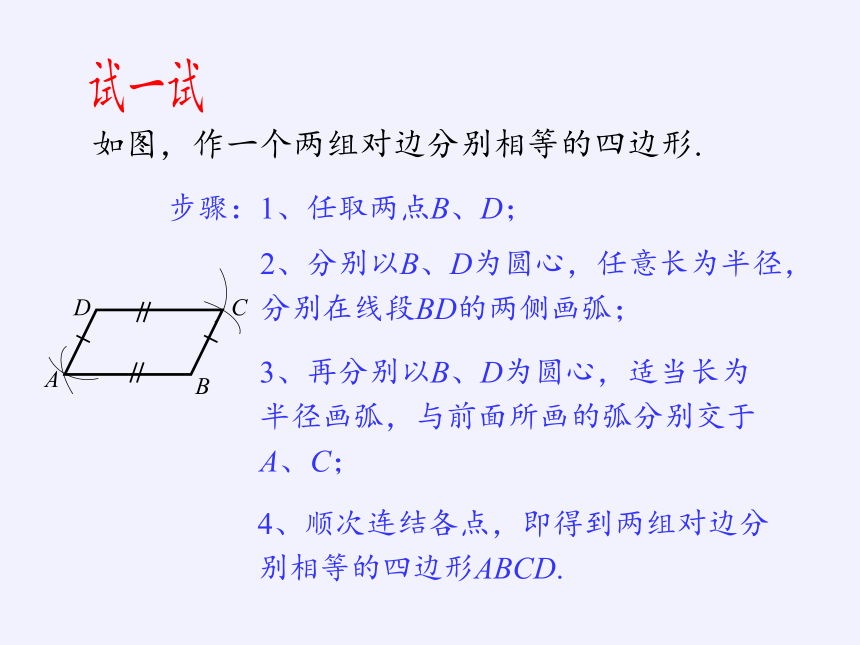
试一试
D
A
B
C
如图,作一个两组对边分别相等的四边形.
步骤:1、任取两点B、D;
2、分别以B、D为圆心,任意长为半径,分别在线段BD的两侧画弧;
3、再分别以B、D为圆心,适当长为半径画弧,与前面所画的弧分别交于A、C;
4、顺次连结各点,即得到两组对边分别相等的四边形ABCD.
求证:四边形ABCD是平行四边形。
已知:在四边形ABCD中, AD=BC,AB=CD.
结论
两组对边分别相等的四边形是平行四边形。
B
D
C
A
B
D
C
A
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而作辅助线,用全等三角形来证明相应的角相等.
证明:连接AC.
∵ AB=CD,BC=DA,AC=CA,
∴ △ABC≌△CDA(SSS).
∴∠1=∠2, ∠3=∠4.
∴AB∥CD,CB∥AD.
∴四边形ABCD是平行四边形.
1
2
3
4
思考
如果只知道四边形的一组对边相等呢?
一组对边边相等
+
平行四边形
?
这组对边也平行
猜想
如图,作一个有一组对边平行且相等的四边形.
1、任意画两条平行线m、n;
2、在直线m、n上分别截取AB、CD,使AB=CD;
3、连结AD、BC,即得到有一组对边平行且相等的四边形ABCD。
A
D
C
B
猜想:
四边形ABCD是哪一种特殊的四边形?
由此,你能得到什么结论?
试一试
m
n
求证:四边形ABCD是平行四边形。
已知:在四边形ABCD中,AD BC。
结论
一组对边平行且相等的四边形是平行四边形。
B
D
C
A
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别相等,从而作辅助线,用全等三角形来证明相应的边相等.
证明:连接AC.
∵ AB∥CD,
∴ ∠1=∠2.
∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS)
∴四边形ABCD是平行四边形.
∴BC=DA.
B
D
C
A
1
2
在下列条件中,不能判定四边形是平行四边形的是( )
(A)AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
试一试:
A
B
C
D
例:已知:平行四边形ABCD中,E,F分别在边BC,DA上,且AF=CE。
求证:四边形AECF是平行四边形
思考:
1.你还有其他的证法吗?
2.哪种方法比较简便呢?
B
C
D
A
F
E
证明:
∴AD∥CB,即AF∥CE.
∵ AF=CE,
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,
1.如图,四边形ABCD,
⑴若AB∥CD,______,
则得 ABCD;
⑵若AB=CD,______,
则得 ABCD;
并分别说出为什么。
A
B
C
D
2.一组对边平行,一组对边相等的四边形是平行四边形吗?
练兵场
如图,AC∥ED,点B在AC上,且AB=ED=BC。找出图中的平行四边形。
A
C
B
E
D
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
小游戏:看谁反应快?
A
B
C
以三角形任两边为邻边作平行四边形可作3个。
D
A
B
C
A
B
C
D
B
C
D
A
P85 练习 第2、3题
两组对边分别平行
两组对边分别相等
一组对边平行且相等
平行四边形
作业
结束
谢 谢
18.2 平行四边形的判定
Contents
目录
02
03
04
学习目标
新知探究
随堂练习
05
课堂小结
01
旧知回顾
边
对边平行
对边相等
角
对角相等
邻角互补
对角线
对角线互相平分
2、平行四边形的性质
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形。
平行四边形的性质
1.理解并掌握平行四边形的判定方法(定义法、判定定理一、定理二);
2.能运用这三种方法来证明一个四边形是平行四边形.
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
根据定义是一种最基本、最重要的判定方法。
思考
平行四边形的两组对边分别相等
你能说出它的逆命题吗?
两组对边分别相等的四边形是平行四边形。
它是一个真命题吗?
试一试
D
A
B
C
如图,作一个两组对边分别相等的四边形.
步骤:1、任取两点B、D;
2、分别以B、D为圆心,任意长为半径,分别在线段BD的两侧画弧;
3、再分别以B、D为圆心,适当长为半径画弧,与前面所画的弧分别交于A、C;
4、顺次连结各点,即得到两组对边分别相等的四边形ABCD.
求证:四边形ABCD是平行四边形。
已知:在四边形ABCD中, AD=BC,AB=CD.
结论
两组对边分别相等的四边形是平行四边形。
B
D
C
A
B
D
C
A
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而作辅助线,用全等三角形来证明相应的角相等.
证明:连接AC.
∵ AB=CD,BC=DA,AC=CA,
∴ △ABC≌△CDA(SSS).
∴∠1=∠2, ∠3=∠4.
∴AB∥CD,CB∥AD.
∴四边形ABCD是平行四边形.
1
2
3
4
思考
如果只知道四边形的一组对边相等呢?
一组对边边相等
+
平行四边形
?
这组对边也平行
猜想
如图,作一个有一组对边平行且相等的四边形.
1、任意画两条平行线m、n;
2、在直线m、n上分别截取AB、CD,使AB=CD;
3、连结AD、BC,即得到有一组对边平行且相等的四边形ABCD。
A
D
C
B
猜想:
四边形ABCD是哪一种特殊的四边形?
由此,你能得到什么结论?
试一试
m
n
求证:四边形ABCD是平行四边形。
已知:在四边形ABCD中,AD BC。
结论
一组对边平行且相等的四边形是平行四边形。
B
D
C
A
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别相等,从而作辅助线,用全等三角形来证明相应的边相等.
证明:连接AC.
∵ AB∥CD,
∴ ∠1=∠2.
∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS)
∴四边形ABCD是平行四边形.
∴BC=DA.
B
D
C
A
1
2
在下列条件中,不能判定四边形是平行四边形的是( )
(A)AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠C
D
试一试:
A
B
C
D
例:已知:平行四边形ABCD中,E,F分别在边BC,DA上,且AF=CE。
求证:四边形AECF是平行四边形
思考:
1.你还有其他的证法吗?
2.哪种方法比较简便呢?
B
C
D
A
F
E
证明:
∴AD∥CB,即AF∥CE.
∵ AF=CE,
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,
1.如图,四边形ABCD,
⑴若AB∥CD,______,
则得 ABCD;
⑵若AB=CD,______,
则得 ABCD;
并分别说出为什么。
A
B
C
D
2.一组对边平行,一组对边相等的四边形是平行四边形吗?
练兵场
如图,AC∥ED,点B在AC上,且AB=ED=BC。找出图中的平行四边形。
A
C
B
E
D
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
小游戏:看谁反应快?
A
B
C
以三角形任两边为邻边作平行四边形可作3个。
D
A
B
C
A
B
C
D
B
C
D
A
P85 练习 第2、3题
两组对边分别平行
两组对边分别相等
一组对边平行且相等
平行四边形
作业
结束
谢 谢
