华东师大版八年级下册数学 19.1.1 矩形的性质 课件(共15张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.1.1 矩形的性质 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 07:49:18 | ||
图片预览

文档简介
(共15张PPT)
八年级 数学下册 (华师大版)
§19.1.1 矩形的性质
矩形的定义
B
D
C
A
∟
有一个角是 角的 形
叫做矩形.
平行四边
直
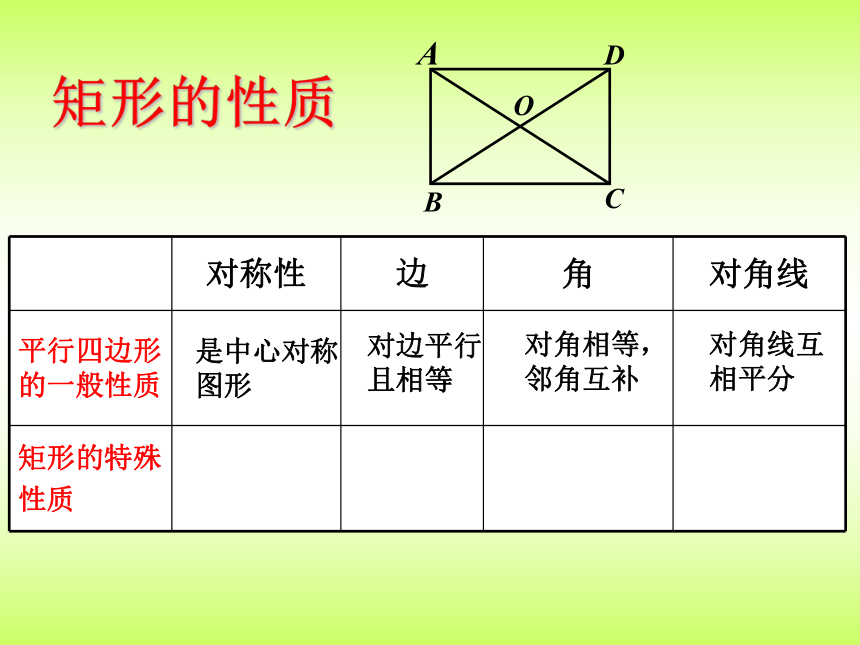
矩形的性质
A
B
C
D
O
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊
性质
是中心对称图形
对边平行且相等
对角相等,邻角互补
对角线互相平分
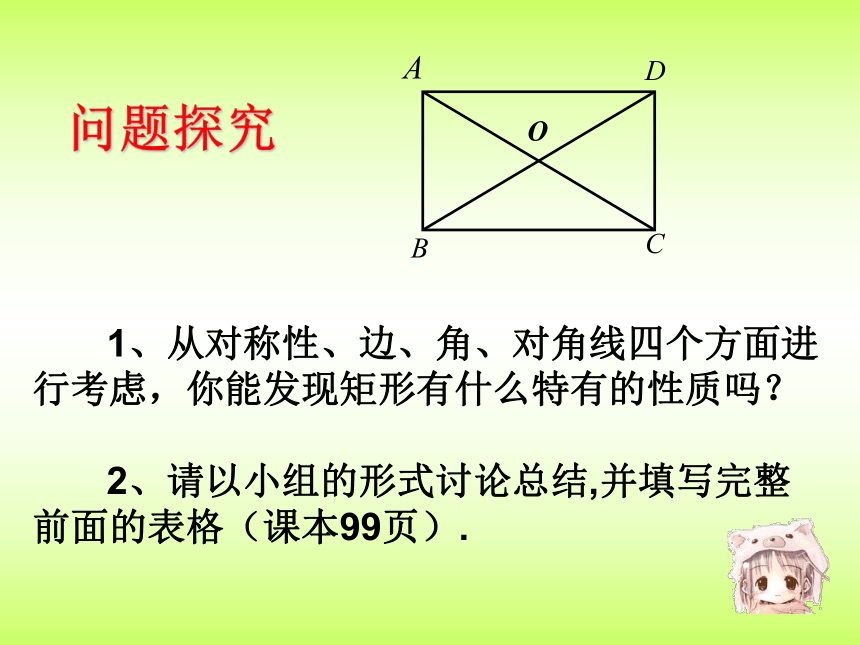
问题探究
1、从对称性、边、角、对角线四个方面进
行考虑,你能发现矩形有什么特有的性质吗?
2、请以小组的形式讨论总结,并填写完整
前面的表格(课本99页).
A
B
C
D
O
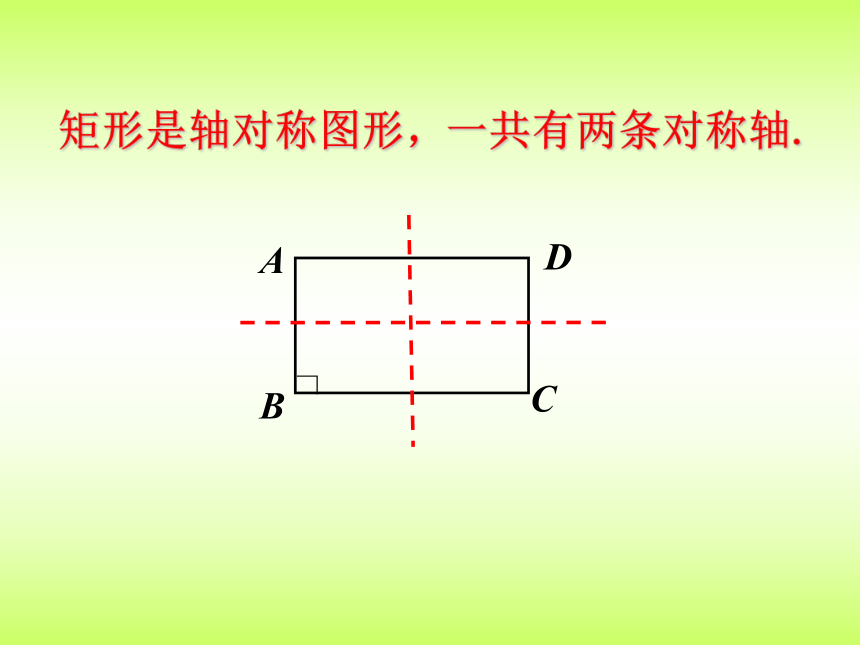
矩形是轴对称图形,
B
D
C
A
∟
一共有两条对称轴.
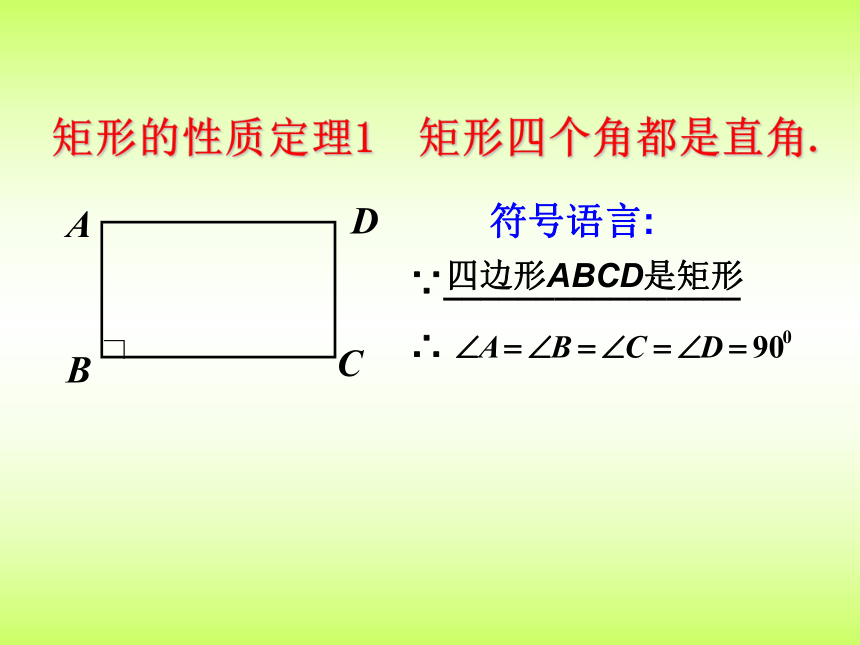
矩形的性质定理1 矩形四个角都是直角.
B
D
C
A
∟
符号语言:
∵________________
∴
四边形ABCD是矩形
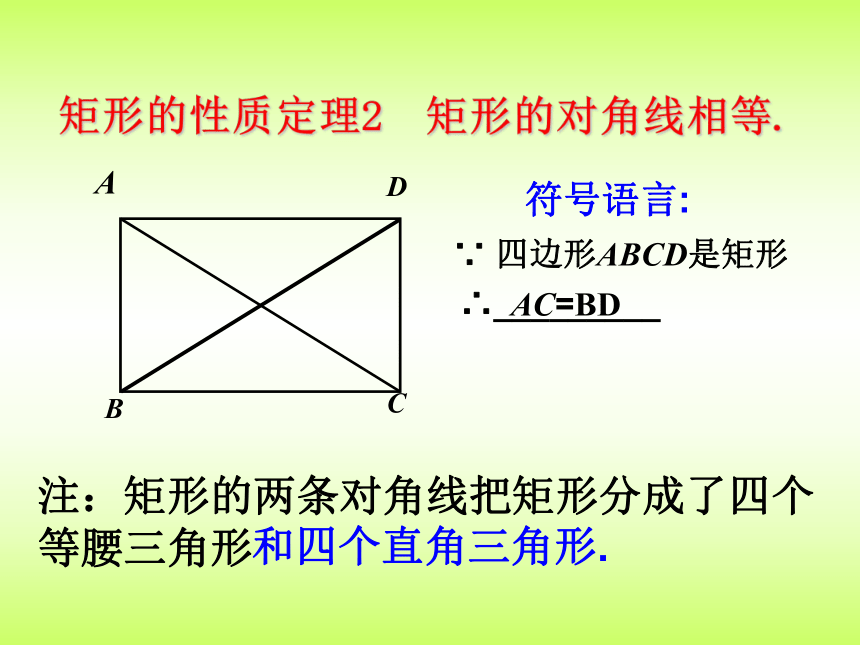
矩形的性质定理2 矩形的对角线相等.
注:矩形的两条对角线把矩形分成了四个
等腰三角形
符号语言:
∵ 四边形ABCD是矩形
∴_________
和四个直角三角形.
AC=BD
A
B
C
D
矩形的性质
A
B
C
D
O
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊
性质
中心对称图形
对边平行且相等
对角相等,邻角互补
对角线互相平分
轴对称图形
邻边垂直
四个角都是直角
对角线相等
例1、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°, AB=4cm, 求矩形对角线的长.
A
B
C
D
O
例1、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°, AB=4cm, 求矩形对角线的长.
变式:如图,矩形ABCD的两条对角线相交于点O,AC=8cm , 求AB的长.
请你再添加一个条件求出AB的长.
A
B
C
D
O
在研究与矩形有关的计算和证明时,
常用到OA=OB=OC=OD及直角三角形的
一些性质,从而把与矩形有关的问题转化
为等腰三角形(等边三角形)或直角三角
形问题来解决.
温馨点拨
A
B
C
D
O
当堂测试
1、矩形具有而平行四边形不具有的性质是( )
A、两组对边分别平行 B、对角相等
C、对角线互相平分 D、对角线相等
2、下列性质中,矩形不一定具有的是 ( )
A、对角线相等 B、四个角都相等
C、对角线垂直 D、是轴对称图形
3、如图,矩形ABCD中,
已知AB=6cm , BC=8cm,
则AC= cm,
OB= cm .
A
B
C
D
O
4、如图所示,矩形ABCD一个角的平分线BE分矩形的一边AD为3cm和1cm两部分,则这个矩形的面积为 .
B
D
C
A
∟
E
5、如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是86cm,矩形的对角线长是13cm , 那么该矩形的周长是 .
A
B
C
D
O
课堂小结
你有什么收获或感想?你还有什么疑问?
八年级 数学下册 (华师大版)
§19.1.1 矩形的性质
矩形的定义
B
D
C
A
∟
有一个角是 角的 形
叫做矩形.
平行四边
直
矩形的性质
A
B
C
D
O
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊
性质
是中心对称图形
对边平行且相等
对角相等,邻角互补
对角线互相平分
问题探究
1、从对称性、边、角、对角线四个方面进
行考虑,你能发现矩形有什么特有的性质吗?
2、请以小组的形式讨论总结,并填写完整
前面的表格(课本99页).
A
B
C
D
O
矩形是轴对称图形,
B
D
C
A
∟
一共有两条对称轴.
矩形的性质定理1 矩形四个角都是直角.
B
D
C
A
∟
符号语言:
∵________________
∴
四边形ABCD是矩形
矩形的性质定理2 矩形的对角线相等.
注:矩形的两条对角线把矩形分成了四个
等腰三角形
符号语言:
∵ 四边形ABCD是矩形
∴_________
和四个直角三角形.
AC=BD
A
B
C
D
矩形的性质
A
B
C
D
O
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊
性质
中心对称图形
对边平行且相等
对角相等,邻角互补
对角线互相平分
轴对称图形
邻边垂直
四个角都是直角
对角线相等
例1、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°, AB=4cm, 求矩形对角线的长.
A
B
C
D
O
例1、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°, AB=4cm, 求矩形对角线的长.
变式:如图,矩形ABCD的两条对角线相交于点O,AC=8cm , 求AB的长.
请你再添加一个条件求出AB的长.
A
B
C
D
O
在研究与矩形有关的计算和证明时,
常用到OA=OB=OC=OD及直角三角形的
一些性质,从而把与矩形有关的问题转化
为等腰三角形(等边三角形)或直角三角
形问题来解决.
温馨点拨
A
B
C
D
O
当堂测试
1、矩形具有而平行四边形不具有的性质是( )
A、两组对边分别平行 B、对角相等
C、对角线互相平分 D、对角线相等
2、下列性质中,矩形不一定具有的是 ( )
A、对角线相等 B、四个角都相等
C、对角线垂直 D、是轴对称图形
3、如图,矩形ABCD中,
已知AB=6cm , BC=8cm,
则AC= cm,
OB= cm .
A
B
C
D
O
4、如图所示,矩形ABCD一个角的平分线BE分矩形的一边AD为3cm和1cm两部分,则这个矩形的面积为 .
B
D
C
A
∟
E
5、如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是86cm,矩形的对角线长是13cm , 那么该矩形的周长是 .
A
B
C
D
O
课堂小结
你有什么收获或感想?你还有什么疑问?
