切线长定理

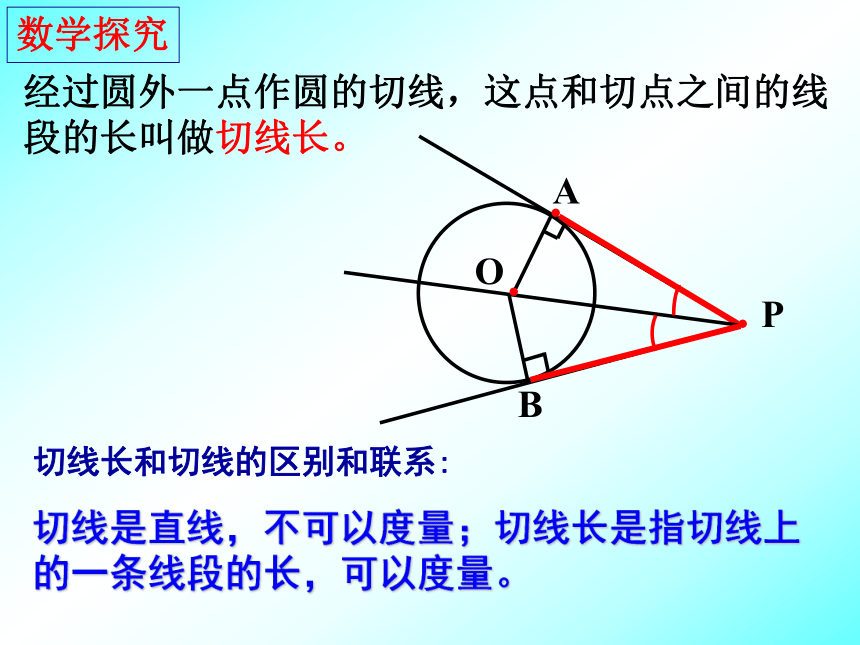
课件38张PPT。切线长定理经过圆外一点作圆的切线，这点和切点之间的线段的长叫做切线长。数学探究O·切线长和切线的区别和联系:
切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量。一、判断
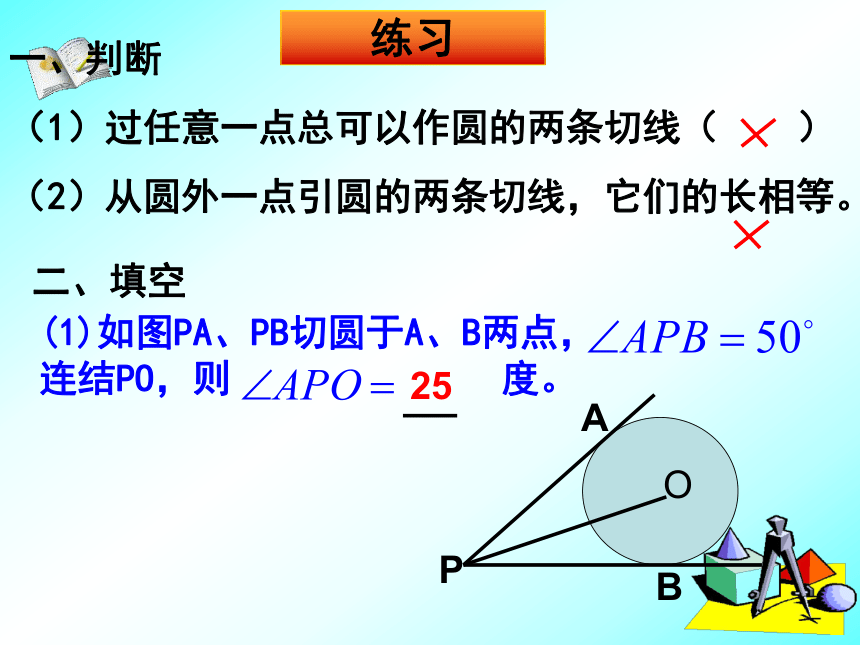
（1）过任意一点总可以作圆的两条切线（ ）
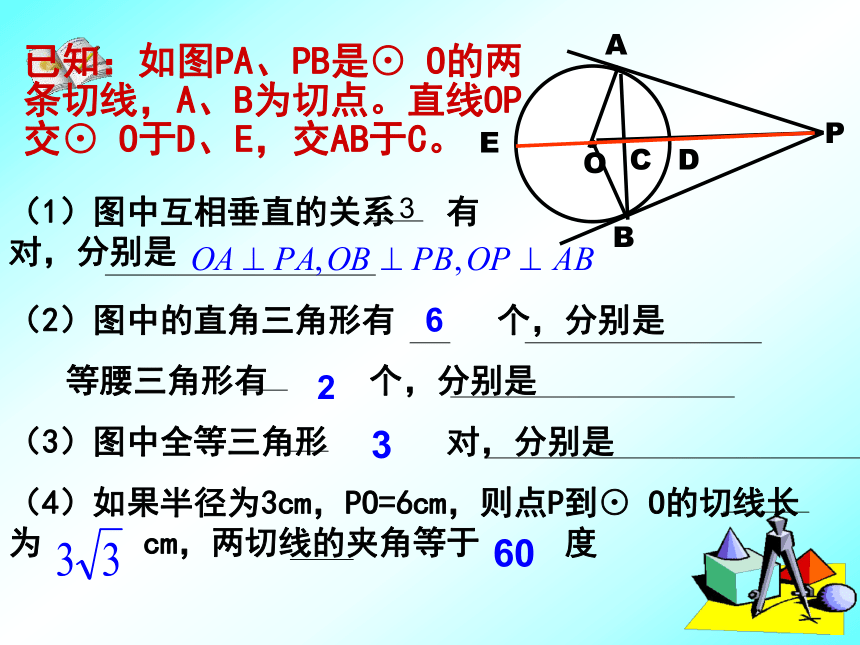
（2）从圆外一点引圆的两条切线，它们的长相等。　　　练习(1)如图PA、PB切圆于A、B两点， 连结PO，则 度。PBOA二、填空25例.PA、PB是⊙O的两条切线，A、B为切点，直线OP交于⊙O于点D、E，交AB于C。
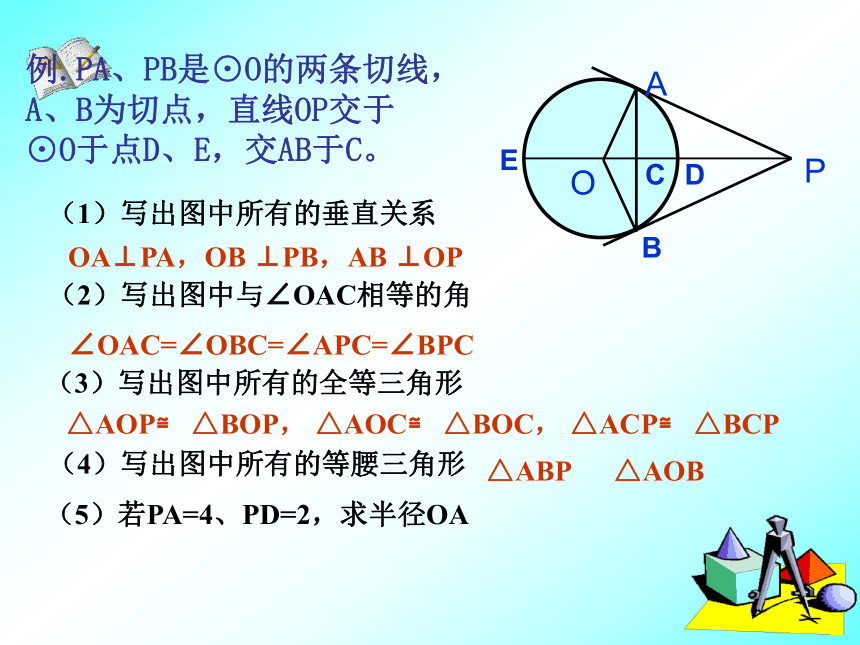
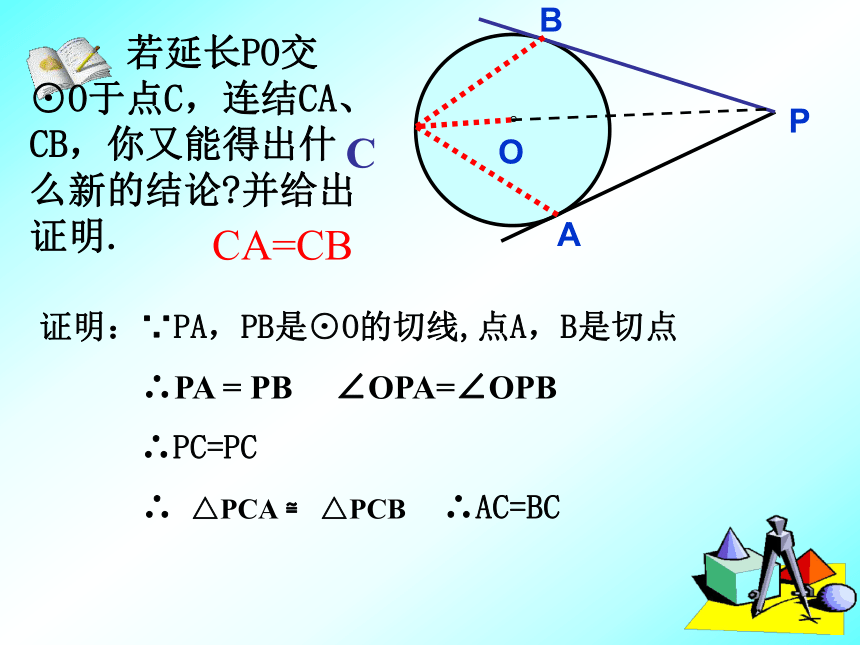
BAPOCED（1）写出图中所有的垂直关系OA⊥PA，OB ⊥PB，AB ⊥OP（3）写出图中所有的全等三角形△AOP≌ △BOP， △AOC≌ △BOC， △ACP≌ △BCP（4）写出图中所有的等腰三角形△ABP △AOB（5）若PA=4、PD=2，求半径OA（2）写出图中与∠OAC相等的角∠OAC=∠OBC=∠APC=∠BPCAPO。B 若延长PO交⊙O于点C，连结CA、CB，你又能得出什么新的结论?并给出证明.CA=CB证明：∵PA，PB是⊙O的切线,点A，B是切点
∴PA = PB ∠OPA=∠OPB
∴PC=PC
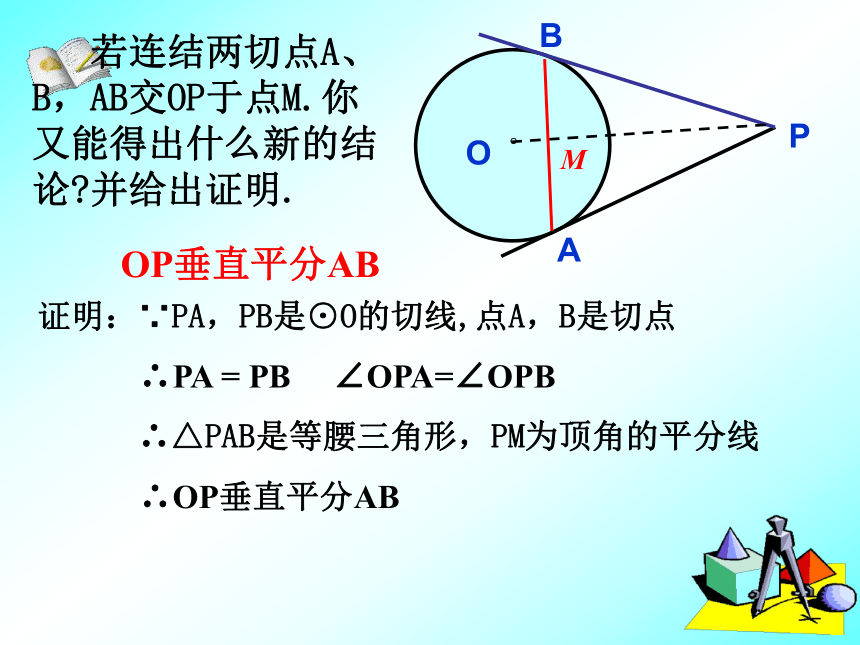
∴ △PCA ≌ △PCB ∴AC=BCCAPO。B 若连结两切点A、B，AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明：∵PA，PB是⊙O的切线,点A，B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形，PM为顶角的平分线
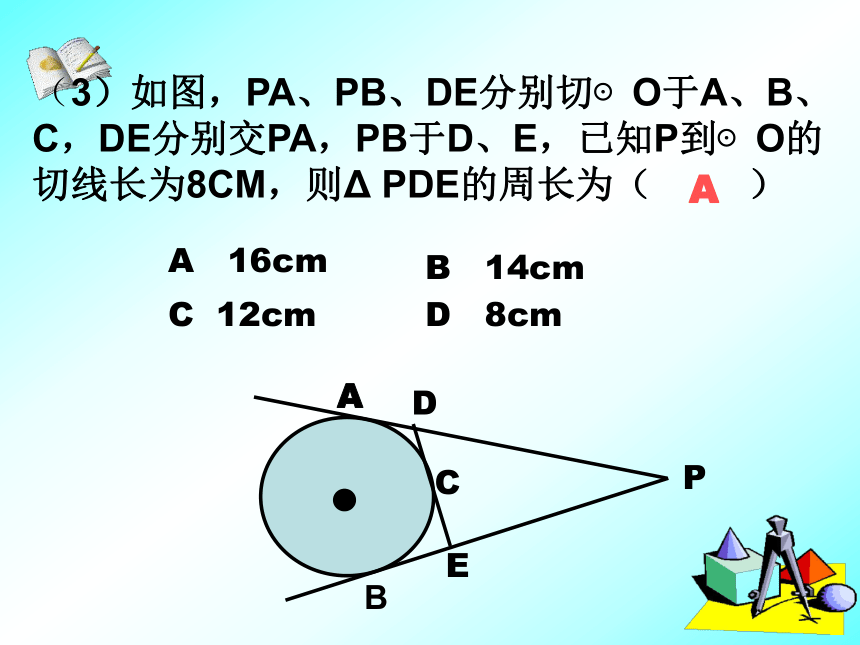
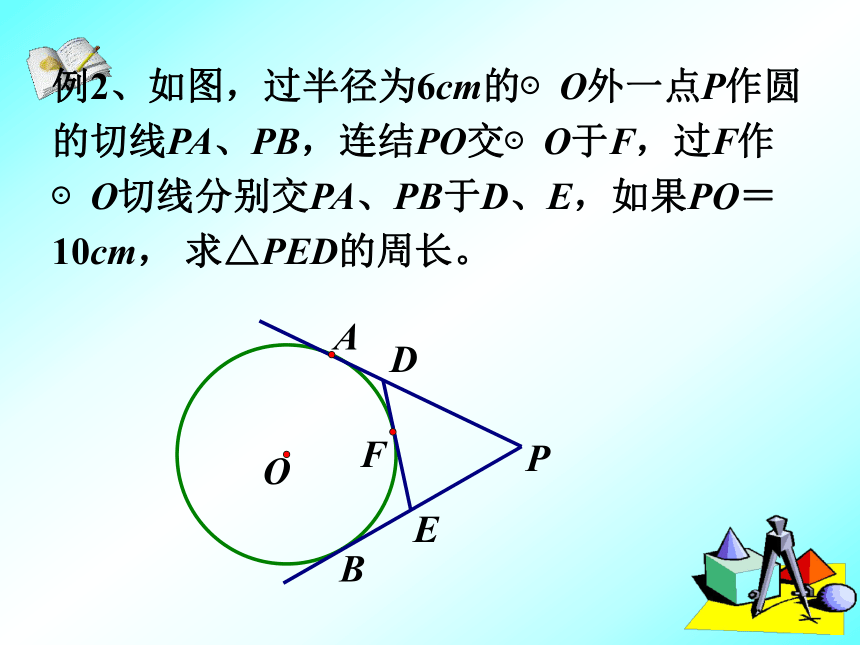
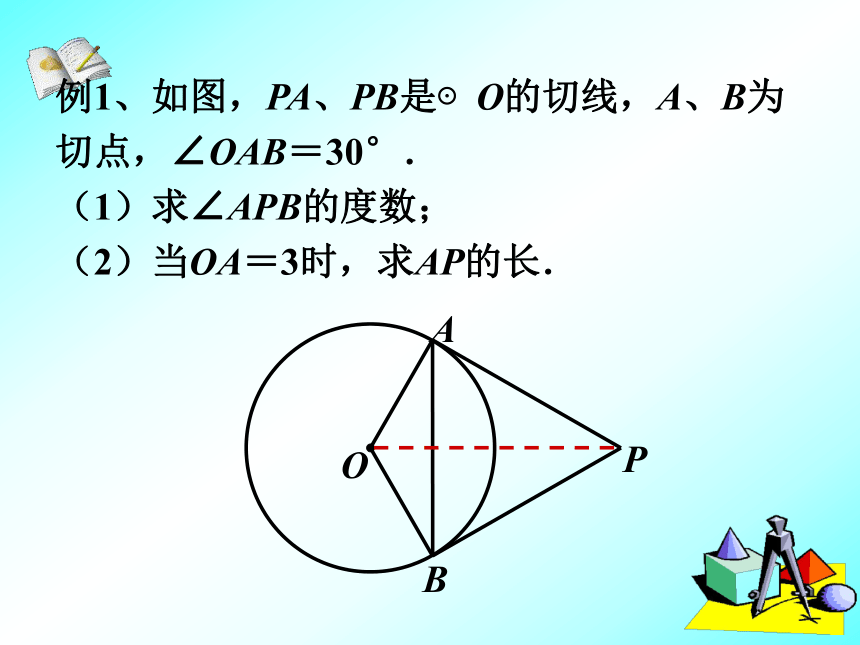
∴OP垂直平分AB（3）如图，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8CM，则Δ PDE的周长为（ ）AA 16cmD 8cmC 12cmB 14cmDCBEAP例2、如图，过半径为6cm的⊙O外一点P作圆的切线PA、PB，连结PO交⊙O于F，过F作⊙O切线分别交PA、PB于D、E，如果PO＝10cm， 求△PED的周长。例1、如图，PA、PB是⊙O的切线，A、B为切点，∠OAB＝30°．
（1）求∠APB的度数；
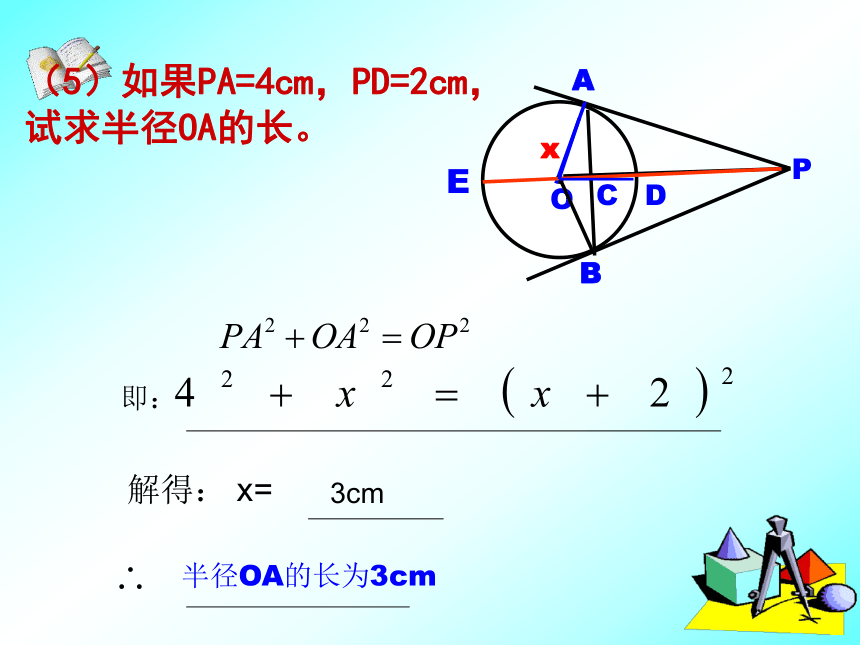
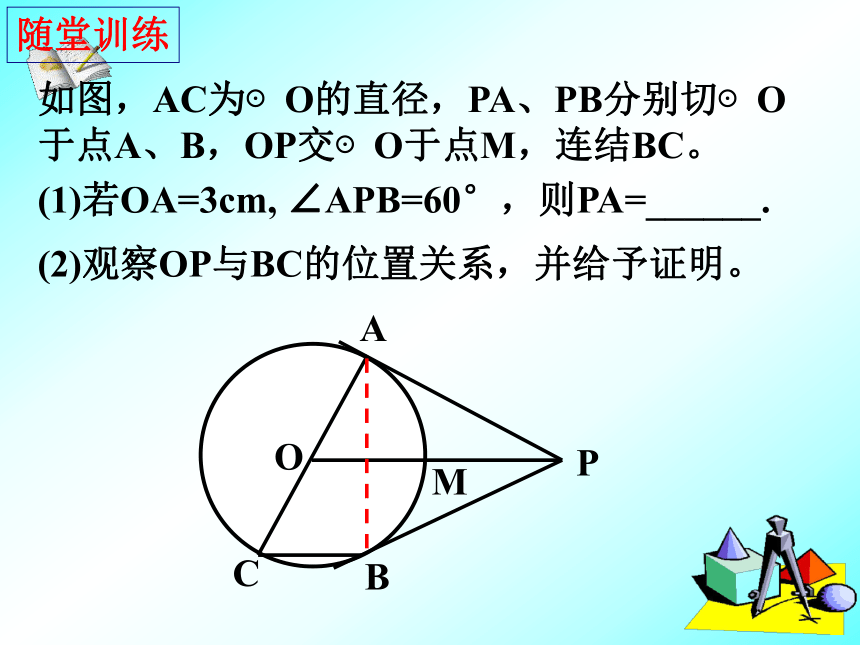
（2）当OA＝3时，求AP的长． （5）如果PA=4cm，PD=2cm，试求半径OA的长。x即：解得： x=3cm半径OA的长为3cm随堂训练(2)观察OP与BC的位置关系，并给予证明。(1)若OA=3cm, ∠APB=60°，则PA=______.如图，AC为⊙O的直径，PA、PB分别切⊙O于点A、B，OP交⊙O于点M，连结BC。已知：如图PA、PB是⊙ O的两条切线，A、B为切点。直线OP交⊙ O于D、E，交AB于C。（2）图中的直角三角形有 个，分别是362360试一试：已知：如图，P为⊙O外一点，PA，PB为⊙O的切线，A和B是切点，BC是直径。∠C＝50?，
①求∠APB的度数
②求证：AC∥OP。 （2）如图，Δ ABC的内切圆分别和BC，AC，AB切于D，E，F；如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,
AC= AB= 116cm9cmBDACFE274 例.如图所示PA、PB分别切圆O于A、B，
并与圆O的切线分别相交于C、D，已知
PA=7cm，
(1)求△PCD的周长．
(2) 如果∠P=46°,
求∠COD的度数E思考：当切点F在弧AB上运动时，问△PED的周长、∠DOE的度数是否发生变化，请说明理由。例3、 已知四边形ABCD的边AB、BC、CD、DA分别与⊙O相切于P、Q、M、N，
求证：AB+CD=AD+BC。 思考 如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?ID 练习四 已知：△ABC是⊙O外切三角形，切点为D，E，F。若BC＝14 cm ，AC＝9cm，AB＝13cm。求AF，BD，CE。
? ABCDEFxxyyzz解:设AF=Xcm,BD=Ycm,CE=Zcm则AE=AF=Xcm,DC=BD=Ycm,AE=EC=Zcm依题意得方程组已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,三边长分别是a,b,c.
求⊙O的半径r.
（1）Rt△的三边长与其内切圆半径间的关系13
探究三求直角三角形内切圆的半径探究三求一般三角形内切圆的半径(2)已知:如图,△ABC的面积为S,三边长分别为a,b,c.
求内切圆⊙O的半径r.
14
小练习1.边长为3、4、5的三角形的内切圆的半径为——2. 边长为5、5、6的三角形的内切圆的半径为——3. 已知:△ABC的面积S=4cm,周长等于 10cm.求内切圆⊙O的半径r.例：如图， △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=9cm，BC=14cm，CA=13cm，求AF、BD、CE的长。x13﹣xx13﹣x9﹣x9﹣x例题选讲1、如图，△ABC中,∠ ABC=50°，∠ACB=75 °,点O 是△ABC的内心，求∠ BOC的度数。随堂训练变式：△ABC中,∠ A=40°，点O是△ABC的内心，求∠ BOC的度数。2、△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC的面积。（提示：设内心为O，连接OA、OB、OC。）OACBrrr知识拓展切线长定理
拓展回顾反思2.三角形的内切圆、内心、内心的性质知识拓展拓展一：直角三角形的外接圆与内切圆1.直角三角形外接圆的圆心(外心)在__________，半径为___________.2.直角三角形内切圆的圆心(内心)在__________，半径r=___________.abc斜边中点斜边的一半三角形内部知识拓展3.已知：如图,PA、PB是⊙O的切线，切点分别是A、B，Q为⊙O上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA=12cm，∠P=70°,求：△PEF的周长和∠EOF的大小。知识拓展4.Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.15.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______.22cm课前训练1、已知，如图，PA、PB是⊙O的两条切线，A、B为切点.直线 OP 交 ⊙O 于点 D、E，交 AB 于 C.
（1）写出图中所有的垂直关系；
（2）如果 PA = 4 cm , PD = 2 cm , 求半径
OA的长.知识拓展2.已知：两个同心圆PA、PB是大圆的两条切线，PC、PD是小圆的两条切线，A、B、C、D为切点。求证：AC=BD试一试：如图△ABC中，∠C＝90?，AC＝6，BC＝8，三角形三边与⊙O均相切，切点分别是D、E、F，求⊙O的半径。 1、如图，一圆内切于四边形ABCD，且AB=16，CD=10，则四边形的周长为( )
（A）50 （B） 52 （C）54 （D） 56巩固练习：2、已知：在△ABC中，BC＝14cm，AC＝9cm，AB＝13cm，BC，AC，AB分别与⊙O切于点D、E、F，求AF，BD和CE的长。 3、以正方形ABCD的一边BC为直径的半圆上有一个动点K，过点K作半圆的切线EF，EF分别交AB、CD于点E、F，试问：四边形AEFD的周长是否会因K点的变动而变化？为什么？4、如图，在梯形ABCD中，AD//BC，AB⊥BC，以AB为直径的⊙O与DC相切于E．已知AB=8，边BC比AD大6，
求边AD、BC的长。