北师大版六年级数学下册 1.3 圆柱的体积 上课课件(共19张PPT)
文档属性
| 名称 | 北师大版六年级数学下册 1.3 圆柱的体积 上课课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第 一 单元 圆柱与圆锥
第 3 课时 圆柱的体积
北师大版六年级数学下册 上课课件
学习目标
1.运用转化的策略,引导学生借助圆面积计算公式的推导方法来推导圆柱的体积计算公式,并理解这个过程。会用圆柱的体积计算公式计算圆柱形物体的体积和容积,运用公式解决一些简单的问题。
2.引导学生逐步学会转化的数学思想和数学方法,培养学生解决实际问题的能力。
3.借助实物演示,培养学生抽象、概括的思维能力。
学习重点 难点
重点:
理解和掌握圆柱体的体积计算公式。
难点:
圆柱体体积计算公式的推导。
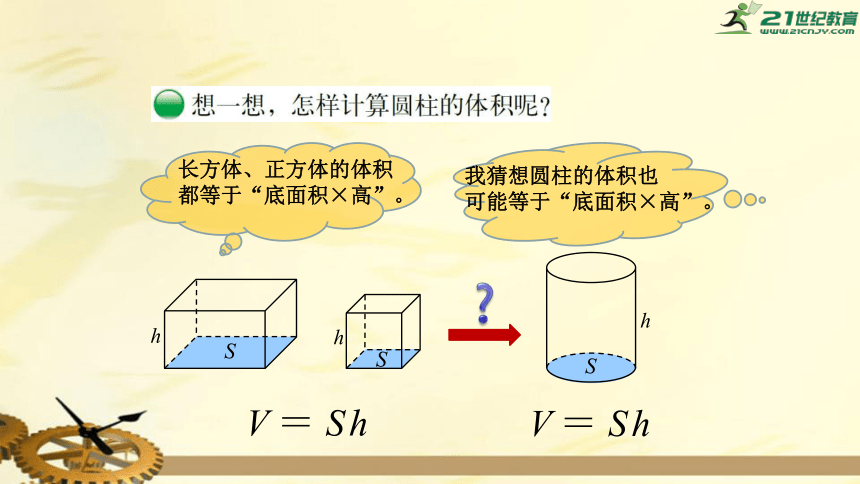
长方体、正方体的体积
都等于“底面积×高”。
我猜想圆柱的体积也
可能等于“底面积×高”。
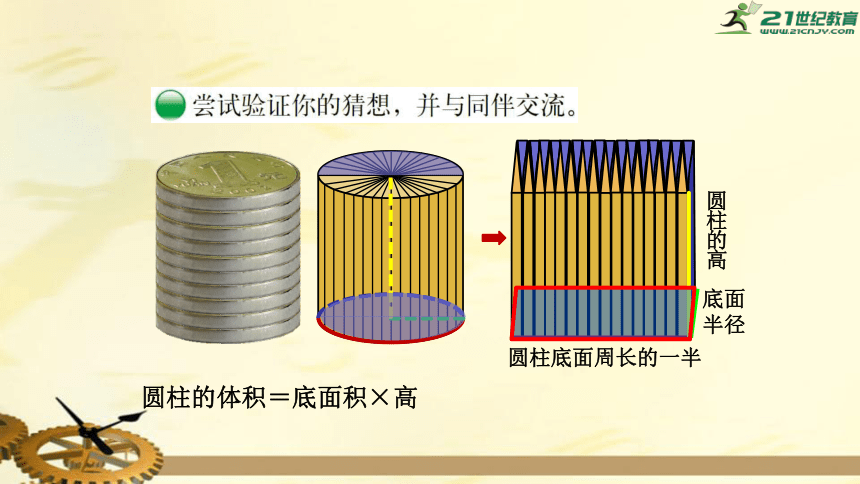
圆柱的体积=底面积×高
圆柱底面周长的一半
圆柱的高
底面
半径
3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:一个杯子能装452.16毫升水。
底面半径:
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
12.56÷3.14÷2=2(cm)
底面积:
3.14×22=12.56(cm )
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512cm3。
如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9g,这根金箍棒的质量为多少千克?
7.9×2512=19844.8(g)=19.8448(kg)
答:这根金箍棒重19.8448千克。
1.分别计算下列各图形的体积,再说说这几个图形
体积计算方法之间的联系。
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×(5÷2)2×8
=157(cm3)
2.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×(6÷2)2×10
=282.6(dm3)
3.这个杯子能否装下3000mL的牛奶?
3.14×(14÷2)2×20
=3077.2(cm3)
=3077.2(mL)
3077.2mL>3000mL
答:这个杯子能装下3000mL的牛奶。
4.光明村李大伯家挖一口圆柱形的水井,底面周长
是3.14m,深是4m。挖出了多少立方米的土?
3.14×(3.14÷3.14÷2)2×4=3.14(m3)
答:挖出了3.14立方米的土。
5.一个装满稻谷的圆柱形粮囤,底面面积为2m2,高
为80cm。每立方米稻谷的质量约为700kg,这个粮囤存放的稻谷的质量约为多少千克?
80cm=0.8m
2×0.8×700=1120(kg)
答:这个粮囤存放的稻谷的质量约为1120千克。
6.下面的长方体和圆柱哪个体积大?说说你的比较方法。
长方体体积为4×4×6=96(dm3)
圆柱体积为3.14×22×6=75.36(dm3)
96>75.36 长方体的体积大
7.如图,求出小铁块的体积。
2cm
2cm
10cm
3.14×(10÷2)2×2
=157(cm3)
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第 一 单元 圆柱与圆锥
第 3 课时 圆柱的体积
北师大版六年级数学下册 上课课件
学习目标
1.运用转化的策略,引导学生借助圆面积计算公式的推导方法来推导圆柱的体积计算公式,并理解这个过程。会用圆柱的体积计算公式计算圆柱形物体的体积和容积,运用公式解决一些简单的问题。
2.引导学生逐步学会转化的数学思想和数学方法,培养学生解决实际问题的能力。
3.借助实物演示,培养学生抽象、概括的思维能力。
学习重点 难点
重点:
理解和掌握圆柱体的体积计算公式。
难点:
圆柱体体积计算公式的推导。
长方体、正方体的体积
都等于“底面积×高”。
我猜想圆柱的体积也
可能等于“底面积×高”。
圆柱的体积=底面积×高
圆柱底面周长的一半
圆柱的高
底面
半径
3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:一个杯子能装452.16毫升水。
底面半径:
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
12.56÷3.14÷2=2(cm)
底面积:
3.14×22=12.56(cm )
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512cm3。
如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9g,这根金箍棒的质量为多少千克?
7.9×2512=19844.8(g)=19.8448(kg)
答:这根金箍棒重19.8448千克。
1.分别计算下列各图形的体积,再说说这几个图形
体积计算方法之间的联系。
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×(5÷2)2×8
=157(cm3)
2.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×(6÷2)2×10
=282.6(dm3)
3.这个杯子能否装下3000mL的牛奶?
3.14×(14÷2)2×20
=3077.2(cm3)
=3077.2(mL)
3077.2mL>3000mL
答:这个杯子能装下3000mL的牛奶。
4.光明村李大伯家挖一口圆柱形的水井,底面周长
是3.14m,深是4m。挖出了多少立方米的土?
3.14×(3.14÷3.14÷2)2×4=3.14(m3)
答:挖出了3.14立方米的土。
5.一个装满稻谷的圆柱形粮囤,底面面积为2m2,高
为80cm。每立方米稻谷的质量约为700kg,这个粮囤存放的稻谷的质量约为多少千克?
80cm=0.8m
2×0.8×700=1120(kg)
答:这个粮囤存放的稻谷的质量约为1120千克。
6.下面的长方体和圆柱哪个体积大?说说你的比较方法。
长方体体积为4×4×6=96(dm3)
圆柱体积为3.14×22×6=75.36(dm3)
96>75.36 长方体的体积大
7.如图,求出小铁块的体积。
2cm
2cm
10cm
3.14×(10÷2)2×2
=157(cm3)
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
