人教A版(2019)选修第三册第七章第四节课时2超几何分布word版含答案
文档属性
| 名称 | 人教A版(2019)选修第三册第七章第四节课时2超几何分布word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 551.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 17:55:47 | ||
图片预览



文档简介
人教A版(2019) 选修第三册 第七章 第四节 课时2 超几何分布
一、单选题
1.袋中有除颜色外完全相同的3个白球和2个红球,从中任取2个,那么下列事件中发生的概率为的是( )
A.都不是白球
B.恰有1个白球
C.至少有1个白球
D.至多有1个白球
2.有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数的数学期望值是
A.n B. C. D.
3.根据某医疗研究所的调查,某地区居民血型的分布为型,型,型,型.现有一血液为型病人需要输血,若在该地区任选一人,那么能为病人输血的概率为( )
A. B.
C. D.
4.由12名志愿者组成的医疗队中,有5名共产党员,现从中任选6人参加抗洪抢险,用随机变量表示这6人中共产党员的人数,则式子表示下列概率 的是( )
A. B. C. D.
5.盒子里共有个除了颜色外完全相同的球,其中有个红球个白球,从盒子中任取个球,则恰好取到个红球个白球的概率为.
A. B. C. D.
6.口袋中装有一些大小相同的红球和黑球,从中取出2个球.两个球都是红球的概率是,都是黑球的概率是,则取出的2个球中恰好一个红球一个黑球的概率是
A. B.
C. D.
二、双空题
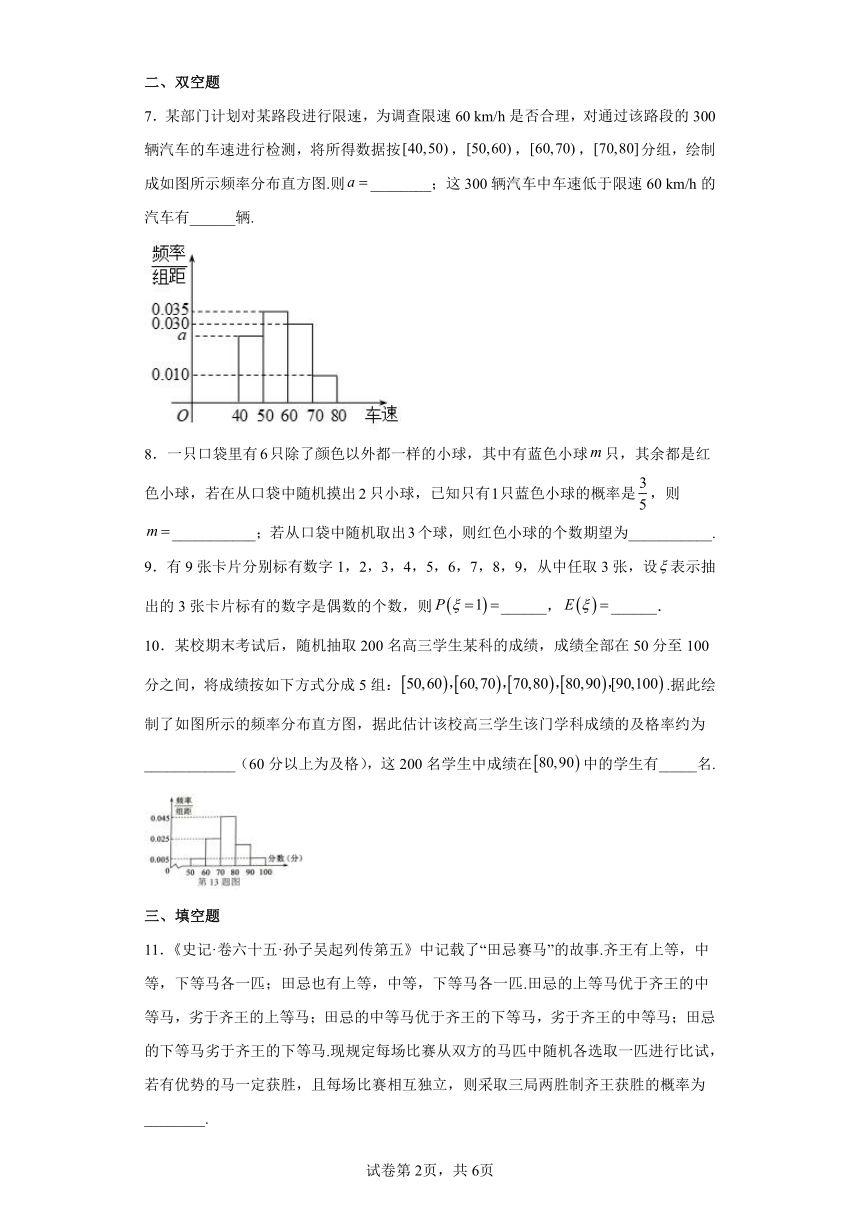
7.某部门计划对某路段进行限速,为调查限速60 km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按,,,分组,绘制成如图所示频率分布直方图.则________;这300辆汽车中车速低于限速60 km/h的汽车有______辆.
8.一只口袋里有只除了颜色以外都一样的小球,其中有蓝色小球只,其余都是红色小球,若在从口袋中随机摸出只小球,已知只有只蓝色小球的概率是,则___________;若从口袋中随机取出个球,则红色小球的个数期望为___________.
9.有9张卡片分别标有数字1,2,3,4,5,6,7,8,9,从中任取3张,设表示抽出的3张卡片标有的数字是偶数的个数,则______,______.
10.某校期末考试后,随机抽取200名高三学生某科的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:.据此绘制了如图所示的频率分布直方图,据此估计该校高三学生该门学科成绩的及格率约为____________(60分以上为及格),这200名学生中成绩在中的学生有_____名.
三、填空题
11.《史记·卷六十五·孙子吴起列传第五》中记载了“田忌赛马”的故事.齐王有上等,中等,下等马各一匹;田忌也有上等,中等,下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.现规定每场比赛从双方的马匹中随机各选取一匹进行比试,若有优势的马一定获胜,且每场比赛相互独立,则采取三局两胜制齐王获胜的概率为________.
12.一个病人服用某种新药后被治愈的概率为0.9.则服用这种新药的4个病人中至少3人被治愈的概率为_______(用数字作答).
四、解答题
13.2019年9月份,在地区新型流感病毒感染者很多.医疗专家采用了一系列的治疗方案对忠者进行医治.研究人员把从采取治疗方案之后的前5天的痊愈人数进行统计得到如下数据:
第天 1 2 3 4 5
痊愈人数人 85 90 100 105 120
(1)现从这5天的数据任选两天进行对比分析,求选取的两天相邻的概率;
(2)经过散点图分析发现表格的数据符合线性回归模型.
(i)请利用所给数据求每日的痊愈人数与的线性回归方程;
(ii)预测第10天的痊愈人数(结果取整,取整即为写成不大于它的最大整数).
参考公式:,.回归直线方程为.
14.某同学参加冬奥会知识有奖问答竞赛,竞赛共设置A,B,C三道题目.已知该同学答对题的概率为,答对题的概率为,答对题的概率为.假设他回答每道题目正确与否是相互独立的.
(1)求该同学所有题目都答对的概率;
(2)设该同学答对题目总数为X,求随机变量X的分布列与数学期望;
(3)若答对,,三题分别得1分,2分,3分,答错均不得分,求该同学总分为3分的概率.
15.某城市随机抽取一个月(天)的空气质量指数监测数据,统计结果如下:
空气质量 优 良 轻微污染 轻度污染 中度污染 中重度污染 重度污染
天数
(1)根据以上数据估计该城市这天空气质量指数的平均值;
(2)若该城市某企业因空气污染每天造成的经济损失(单位:元)与空气质量指数(记为)的关系式为,若在本月天中随机抽取一天,试估计该天经济损失大于元且不超过元的概率.
16.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的1000名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别
频数 2 250 450 290 8
(1)根据样本数据,可近似地认为学生的旅游费用支出服从正态分布.若该所大学共有学生65000人,试估计有多少位同学旅游费用支出在8100元以上;
(2)已知样本数据中旅游费用支出在范围内的8名学生中有5名女生,3名男生,现想选其中3名学生回访,记选出的男生人数为.求的分布列与数学期望.
附:若,则,,.
17.为了弘扬传统文化,某市举办了“高中生诗词大赛”,现从全市参加比赛的学生中随机抽取1000人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为,.
(1)求频率分布直方图中m的值;
(2)在所抽取的1000名学生中,用分层抽样的方法在成绩为的学生中抽取了一个容量为5的样本,再从该样本中任意抽取2人,求2人的成绩均在区间内的概率;
18.新高考的数学试卷第1至第8题为单选“题”,第9至第12题为多选“题”,多选“题”A B C D四个选项中至少有两个选项符合题意,其评分标准如下:全部选对得5分,部分选对得2分,选错或不选得0分,在某次考试中,第10 11 12三题的难度较大,第10题正确选项为BC 第11题正确选项为AD,第12题正确选项为AB,甲 乙两位同学由于考前准备不足,只能对这三道题的选项进行随机选取,每个选项是否被选到是等可能的.
(1)若甲同学每题均随机选取一项,求甲同学三题得分合计为6分的概率;
(2)若乙同学计划每题均随机选取两项,记乙同学的三题得分为,求的分布列及其期望.
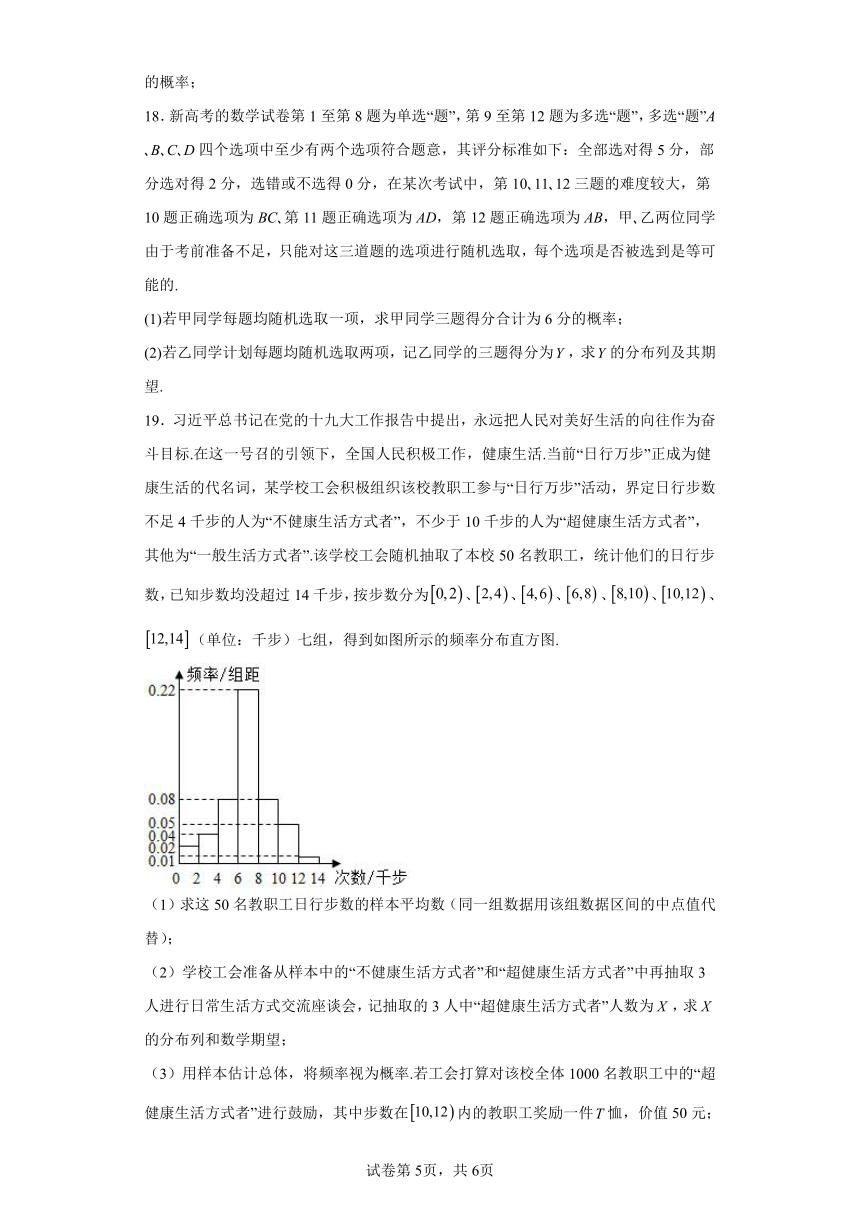
19.习近平总书记在党的十九大工作报告中提出,永远把人民对美好生活的向往作为奋斗目标.在这一号召的引领下,全国人民积极工作,健康生活.当前“日行万步”正成为健康生活的代名词,某学校工会积极组织该校教职工参与“日行万步”活动,界定日行步数不足4千步的人为“不健康生活方式者”,不少于10千步的人为“超健康生活方式者”,其他为“一般生活方式者”.该学校工会随机抽取了本校50名教职工,统计他们的日行步数,已知步数均没超过14千步,按步数分为、、、、、、(单位:千步)七组,得到如图所示的频率分布直方图.
(1)求这50名教职工日行步数的样本平均数(同一组数据用该组数据区间的中点值代替);
(2)学校工会准备从样本中的“不健康生活方式者”和“超健康生活方式者”中再抽取3人进行日常生活方式交流座谈会,记抽取的3人中“超健康生活方式者”人数为,求的分布列和数学期望;
(3)用样本估计总体,将频率视为概率.若工会打算对该校全体1000名教职工中的“超健康生活方式者”进行鼓励,其中步数在内的教职工奖励一件恤,价值50元;步数在内的教职工奖励一件恤和一条运动裤,价值100元;试判断10000元的预算是否足够.
20.某班主任对全班名学生进行了作业量多少与手机网游的调查,数据如下表:
认为作业多 认为作业不多 总数
喜欢手机网游
不喜欢手机网游
总数
(1)若随机地抽问这个班的一名学生,分别求事件“认为作业不多”和事件“喜欢手机网游且认为作业多”的概率;
(2)若在“认为作业多”的学生中已经用分层抽样的方法选取了名学生.现要从这名学生中任取名学生了解情况,求其中恰有名“不喜欢手机网游”的学生的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用概型的概率公式逐个分析求解可得答案
【详解】
P(都不是白球)==,P(恰有1个白球)==,P(至少有1个白球)==,P(至多有1个白球)==.
故选:D.
2.C
【解析】
【详解】
试题分析:先由超几何分布的意义,确定本题中抽到次品数服从超几何分布,再由超几何分布的性质:若随机变量X~H(n,M,N),则其数学期望为,计算抽到的次品数的数学期望值即可
解:设抽到的次品数为X,
则有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数X服从超几何分布
即X~H(n,M,N),
∴抽到的次品数的数学期望值EX=
故选C
点评:本题考查了离散型随机变量的特殊分布列及其性质,超几何分布的意义及其数学期望的求法
3.D
【解析】
由题意可知,能为型病人输血的有型和型,将对应的频率相加可得结果.
【详解】
由题意可知,能为型病人输血的有型和型,
因此,在该地区任选一人,那么能为病人输血的概率为.
故选:D.
4.D
【解析】
【分析】
根据超几何概型公式,分析所给表达式,即可得答案.
【详解】
因为12名志愿者中有5名党员,7名非党员,
所以表示从5名党员中选3名,7名非党员中选3名的概率
所以.
故选:D
5.B
【解析】
【详解】
由题意得所求概率为.选.
6.B
【解析】
分析题意,根据互斥事件、对立事件的概率求解即可得到答案.
【详解】
由题意知,从袋中取出2个球的所有可能情况为:2个都是红球,2个都是黑球,1个红球和1个黑球.
由互斥事件的概率公式可得,取出的2个球中恰好一个红球一个黑球的概率是.
故选B.
【点睛】
求概率时首先要读懂题意,然后选择合适的概率类型求解.在解题时对于一些复杂事件的概率,可转化为若干个互斥事件的和事件的概率求解,属于基础题.
7.
【解析】
【分析】
根据个小矩形面积之和为1即可求出的值;根据频率分布直方图可以求出车速低于限速60 km/h的频率,从而可求出汽车有多少辆.
【详解】
由解得:.
这300辆汽车中车速低于限速60 km/h的汽车有.
故答案为:;.
8. ##
【解析】
【分析】
根据组合计数原理结合古典该型的概率公式可得出关于的等式,即可解得的值;从口袋中随机取出个球,设红色小球的个数为,可知随机变量的可能取值为、、、,求出随机变量在不同取值下的概率,进一步可求得的值.
【详解】
由已知可得,可得,解得,
从口袋中随机取出个球,设红色小球的个数为,则的可能取值为、、、,
则,,,,
因此,.
故答案为:;.
9.
【解析】
【分析】
结合超几何分布计算公式进行求解.
【详解】
由题意知的可能取值分别为0,1,2,3,且,
,,,
则.
故答案为:;
10.
【解析】
先由频率直方图得到60分以下的频率,再用对立事件的概率得到60分以上的频率.先通过频率直方图计算中的频率,再乘以样本容量得到人数.
【详解】
由频率直方图知,60分以下的频率为,
所以60分以上的频率为.
因为中的频率,
所以中的学生有.
故答案为:(1). (2).
【点睛】
本题主要考查样本估计总体中的频率直方图的应用,还考查了运算求解的能力,属于基础题.
11.
【解析】
【分析】
列出所有情况,统计满足条件的情况得到齐王每次胜利的概率,再根据独立事件计算得到答案.
【详解】
设齐王的上中下等马为,田忌的上中下等马为,
则共有9种情况,
其中齐王获胜的有6种情况,故,
.
故答案为:.
【点睛】
本题考查了概率的计算,意在考查学生的计算能力和应用能力.
12.0.9744
【解析】
【分析】
由题意知,本题符合独立重复试验条件,分情况讨论:若共有3人被治愈,若共有4人被治愈,分别代入独立重复试验公式得到结果.最后求和.
【详解】
解:由题意知本题分情况讨论:若共有3人被治愈,则;
若共有4人被治愈,则,
至少有3人被治愈概率.
故答案为:0.9477.
【点睛】
判断是否为独立重复试验的关键是每次试验事件的概率不变,并且每次试验的结果同其他各次试验的结果无关,重复是指试验为一系列的试验,并非一次试验,而是多次,但要注意重复事件发生的概率相互之间没有影响.
13.(1);(2)(i);(ii)159人.
【解析】
【分析】
(1)根据古典概型的概率计算公式,分别用列举法列举出选法总数以及两天相邻的选法数,即可算出;
(2)(i)利用最小二乘法计算出和,即可得出与的线性回归方程;
(ii)根据线性回归方程,令,即可预测第10天的痊愈人数.
【详解】
(1)选取的两天有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种选法,其中这两天相邻共(1,2),(2,3),(3,4),(4,5),所以概率为.
(2)(i)因为,,,,
所以,,
所以回归方程为.
(ii)当时,.
预测第10天的痊愈人数为159人.
【点睛】
本题主要考查古典概型的概率公式的应用,利用最小二乘法求线性回归方程,并利用线性回归方程进行预测,意在考查学生的数学运算能力,属于基础题.
14.(1);(2)分布列见解析,;(3).
【解析】
【分析】
(1)由独立事件同时发生的概率公式即可求解;
(2)可能的取值为,分别求出对应的概率,即可得分布列和数学期望;
(3)由独立事件同时发生的概率公式以及互斥事件的概率公式即可求解.
【详解】
(1)该同学所有题目都答对的概率为,
(2)由题意可得:可能的取值为,
,
,
所以X的分布列为:
,
(3)该同学总分为分得情况为:只答对或只答对,
所以该同学总分为3分的概率:.
15.(1)(2)
【解析】
【详解】
试题分析:(1)根据平均数公式得(2)先确定经济损失大于元且不超过元所对应的范围:由得.再对照表格确定天数,最后根据古典概型概率求法得结果
试题解析:(1)该城市这天空气质量指数的平均值为.
(2)设“在本月天中随机抽取一天,该天经济损失大于元且不超过元” 为事件
由得.根据表格数据得共有天, 所以.
考点:古典概型概率
【方法点睛】古典概型中基本事件数的探求方法
(1)列举法.
(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.
(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.
16.(1)1482;(2)分布列为见解析,数学期望为.
【解析】
【分析】
(1)根据正态分布的公式求得,再乘以总数即可得到结果;
(2)先求出概率,写出分布列,求出数学期望即可.
【详解】
(1)由题意得:,根据正态分布的公式得到:,
再乘以总数得到结果0.0228×65000=1482.
估计有1482位同学旅游费用支出在8100元以上
(2)Y的可能取值为0,1,2,3.
;
;
;
.
Y的分布列为:
Y 0 1 2 3
P
所以,Y的数学期望为:
.
17.(1)0.015;(2).
【解析】
【分析】
根据频率分布直方图中所有小矩形的面积之和等于1列出关于m的方程,解得.
由分层抽样可得成绩在区间的人数为3个,成绩在区间的人数为2个,列出所有抽取2人的情况,可以得到2人的成绩均在区间内只有1种情况,从而根据古典概型概率计算公式求得概率即可.
【详解】
解:依题意可知组距为10,
由,
解得 .
抽取了一个容量为5的样本成绩在区间的人数为: 人,
记3人为a、b、c.
成绩在区间的人数为:人,
记2人为d、e ,
任取2人的基本事件为:ab、ac、ad、ae、bc、bd、be、cd、ce、de,共计10个
其中在区间的基本事件为:de ,共计1个 ,
所以2人的成绩均在区间的概率为:.
【点睛】
有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.
18.(1)
(2)分布列见解析,2.5分
【解析】
【分析】
(1)根据相互独立事件的概率公式进行求解即可;
(2)根据相互独立事件的概率公式,结合数学期望公式进行求解判断即可.
(1)
因为甲同学三题得分合计为6分,所以这三道题每道题得2分,
所以甲同学三题得分合计为6分的概率为:
(2)
乙同学计划每题均随机选取两项,则三题每题可能得分为0分或5分
得5分的概率为,得0分的概率为
乙同学的三道题得分Y的可能取值为0,5,10,15
,
,
所以Y的分布列为:
0 5 10 15
因此分
19.(1);(2)分布列见解析,;(3)足够.
【解析】
【分析】
(1)本题可根据频率分布直方图求出样本平均数;
(2)本题首先可通过频率分布直方图求出“不健康生活方式者”和“超健康生活方式者”的人数,然后求出的所有可能的值以及对应的概率,即可列出的分布列,最后根据的分布列即可求出的数学期望;
(3)本题可通过频率分布直方图求出、内的人数,然后求出奖励所需要的总金额并与进行对比,即可得出结果.
【详解】
(1)由频率分布直方图易知,50名教职工日行步数的样本平均数为:
.
(2)由频率分布直方图易知,50名职工中“不健康生活方式者”和“超健康生活方式者”各有6人,
则的所有可能的值为、、、,
,,
,,
故的分布列为:
0 1 2 3
.
(3)用样本估计总体,步数在内的概率为,有人,
步数在内的概率为,有人,
因为,所以的预算足够.
20.(1)事件“认为作业不多”和事件“喜欢手机网游且认为作业多”的概率分别为、;
(2).
【解析】
【分析】
(1)利用古典概型的概率公式可求得所求事件的概率;
(2)确定所选的名学生中,“不喜欢手机网游”和“喜欢手机网游”的学生人数,加以标记,列举出所有的基本事件,确定所求事件所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率.
(1)
解:由题意可知,全班名学生中,“认为作业不多”的学生人数为人,
“喜欢手机网游且认为作业多”的学生人数为人,
因此,随机地抽问这个班的一名学生,事件“认为作业不多”的概率为,
事件“喜欢手机网游且认为作业多”的概率为.
(2)
解:在“认为作业多”的学生中已经用分层抽样的方法选取了名学生,
这名学生中“不喜欢手机网游”的学生人数为,记为,
名学生中“喜欢手机网游”的学生人数为,分别记为、、、,
从这名学生中任取名学生,所有的基本事件有:、、、、、、、、、,共种,
其中,事件“恰有名“不喜欢手机网游”的学生”包含的基本事件有:、、、,共种,
故所求概率为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.袋中有除颜色外完全相同的3个白球和2个红球,从中任取2个,那么下列事件中发生的概率为的是( )
A.都不是白球
B.恰有1个白球
C.至少有1个白球
D.至多有1个白球
2.有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数的数学期望值是
A.n B. C. D.
3.根据某医疗研究所的调查,某地区居民血型的分布为型,型,型,型.现有一血液为型病人需要输血,若在该地区任选一人,那么能为病人输血的概率为( )
A. B.
C. D.
4.由12名志愿者组成的医疗队中,有5名共产党员,现从中任选6人参加抗洪抢险,用随机变量表示这6人中共产党员的人数,则式子表示下列概率 的是( )
A. B. C. D.
5.盒子里共有个除了颜色外完全相同的球,其中有个红球个白球,从盒子中任取个球,则恰好取到个红球个白球的概率为.
A. B. C. D.
6.口袋中装有一些大小相同的红球和黑球,从中取出2个球.两个球都是红球的概率是,都是黑球的概率是,则取出的2个球中恰好一个红球一个黑球的概率是
A. B.
C. D.
二、双空题
7.某部门计划对某路段进行限速,为调查限速60 km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按,,,分组,绘制成如图所示频率分布直方图.则________;这300辆汽车中车速低于限速60 km/h的汽车有______辆.
8.一只口袋里有只除了颜色以外都一样的小球,其中有蓝色小球只,其余都是红色小球,若在从口袋中随机摸出只小球,已知只有只蓝色小球的概率是,则___________;若从口袋中随机取出个球,则红色小球的个数期望为___________.
9.有9张卡片分别标有数字1,2,3,4,5,6,7,8,9,从中任取3张,设表示抽出的3张卡片标有的数字是偶数的个数,则______,______.
10.某校期末考试后,随机抽取200名高三学生某科的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:.据此绘制了如图所示的频率分布直方图,据此估计该校高三学生该门学科成绩的及格率约为____________(60分以上为及格),这200名学生中成绩在中的学生有_____名.
三、填空题
11.《史记·卷六十五·孙子吴起列传第五》中记载了“田忌赛马”的故事.齐王有上等,中等,下等马各一匹;田忌也有上等,中等,下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.现规定每场比赛从双方的马匹中随机各选取一匹进行比试,若有优势的马一定获胜,且每场比赛相互独立,则采取三局两胜制齐王获胜的概率为________.
12.一个病人服用某种新药后被治愈的概率为0.9.则服用这种新药的4个病人中至少3人被治愈的概率为_______(用数字作答).
四、解答题
13.2019年9月份,在地区新型流感病毒感染者很多.医疗专家采用了一系列的治疗方案对忠者进行医治.研究人员把从采取治疗方案之后的前5天的痊愈人数进行统计得到如下数据:
第天 1 2 3 4 5
痊愈人数人 85 90 100 105 120
(1)现从这5天的数据任选两天进行对比分析,求选取的两天相邻的概率;
(2)经过散点图分析发现表格的数据符合线性回归模型.
(i)请利用所给数据求每日的痊愈人数与的线性回归方程;
(ii)预测第10天的痊愈人数(结果取整,取整即为写成不大于它的最大整数).
参考公式:,.回归直线方程为.
14.某同学参加冬奥会知识有奖问答竞赛,竞赛共设置A,B,C三道题目.已知该同学答对题的概率为,答对题的概率为,答对题的概率为.假设他回答每道题目正确与否是相互独立的.
(1)求该同学所有题目都答对的概率;
(2)设该同学答对题目总数为X,求随机变量X的分布列与数学期望;
(3)若答对,,三题分别得1分,2分,3分,答错均不得分,求该同学总分为3分的概率.
15.某城市随机抽取一个月(天)的空气质量指数监测数据,统计结果如下:
空气质量 优 良 轻微污染 轻度污染 中度污染 中重度污染 重度污染
天数
(1)根据以上数据估计该城市这天空气质量指数的平均值;
(2)若该城市某企业因空气污染每天造成的经济损失(单位:元)与空气质量指数(记为)的关系式为,若在本月天中随机抽取一天,试估计该天经济损失大于元且不超过元的概率.
16.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的1000名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别
频数 2 250 450 290 8
(1)根据样本数据,可近似地认为学生的旅游费用支出服从正态分布.若该所大学共有学生65000人,试估计有多少位同学旅游费用支出在8100元以上;
(2)已知样本数据中旅游费用支出在范围内的8名学生中有5名女生,3名男生,现想选其中3名学生回访,记选出的男生人数为.求的分布列与数学期望.
附:若,则,,.
17.为了弘扬传统文化,某市举办了“高中生诗词大赛”,现从全市参加比赛的学生中随机抽取1000人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为,.
(1)求频率分布直方图中m的值;
(2)在所抽取的1000名学生中,用分层抽样的方法在成绩为的学生中抽取了一个容量为5的样本,再从该样本中任意抽取2人,求2人的成绩均在区间内的概率;
18.新高考的数学试卷第1至第8题为单选“题”,第9至第12题为多选“题”,多选“题”A B C D四个选项中至少有两个选项符合题意,其评分标准如下:全部选对得5分,部分选对得2分,选错或不选得0分,在某次考试中,第10 11 12三题的难度较大,第10题正确选项为BC 第11题正确选项为AD,第12题正确选项为AB,甲 乙两位同学由于考前准备不足,只能对这三道题的选项进行随机选取,每个选项是否被选到是等可能的.
(1)若甲同学每题均随机选取一项,求甲同学三题得分合计为6分的概率;
(2)若乙同学计划每题均随机选取两项,记乙同学的三题得分为,求的分布列及其期望.
19.习近平总书记在党的十九大工作报告中提出,永远把人民对美好生活的向往作为奋斗目标.在这一号召的引领下,全国人民积极工作,健康生活.当前“日行万步”正成为健康生活的代名词,某学校工会积极组织该校教职工参与“日行万步”活动,界定日行步数不足4千步的人为“不健康生活方式者”,不少于10千步的人为“超健康生活方式者”,其他为“一般生活方式者”.该学校工会随机抽取了本校50名教职工,统计他们的日行步数,已知步数均没超过14千步,按步数分为、、、、、、(单位:千步)七组,得到如图所示的频率分布直方图.
(1)求这50名教职工日行步数的样本平均数(同一组数据用该组数据区间的中点值代替);
(2)学校工会准备从样本中的“不健康生活方式者”和“超健康生活方式者”中再抽取3人进行日常生活方式交流座谈会,记抽取的3人中“超健康生活方式者”人数为,求的分布列和数学期望;
(3)用样本估计总体,将频率视为概率.若工会打算对该校全体1000名教职工中的“超健康生活方式者”进行鼓励,其中步数在内的教职工奖励一件恤,价值50元;步数在内的教职工奖励一件恤和一条运动裤,价值100元;试判断10000元的预算是否足够.
20.某班主任对全班名学生进行了作业量多少与手机网游的调查,数据如下表:
认为作业多 认为作业不多 总数
喜欢手机网游
不喜欢手机网游
总数
(1)若随机地抽问这个班的一名学生,分别求事件“认为作业不多”和事件“喜欢手机网游且认为作业多”的概率;
(2)若在“认为作业多”的学生中已经用分层抽样的方法选取了名学生.现要从这名学生中任取名学生了解情况,求其中恰有名“不喜欢手机网游”的学生的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用概型的概率公式逐个分析求解可得答案
【详解】
P(都不是白球)==,P(恰有1个白球)==,P(至少有1个白球)==,P(至多有1个白球)==.
故选:D.
2.C
【解析】
【详解】
试题分析:先由超几何分布的意义,确定本题中抽到次品数服从超几何分布,再由超几何分布的性质:若随机变量X~H(n,M,N),则其数学期望为,计算抽到的次品数的数学期望值即可
解:设抽到的次品数为X,
则有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数X服从超几何分布
即X~H(n,M,N),
∴抽到的次品数的数学期望值EX=
故选C
点评:本题考查了离散型随机变量的特殊分布列及其性质,超几何分布的意义及其数学期望的求法
3.D
【解析】
由题意可知,能为型病人输血的有型和型,将对应的频率相加可得结果.
【详解】
由题意可知,能为型病人输血的有型和型,
因此,在该地区任选一人,那么能为病人输血的概率为.
故选:D.
4.D
【解析】
【分析】
根据超几何概型公式,分析所给表达式,即可得答案.
【详解】
因为12名志愿者中有5名党员,7名非党员,
所以表示从5名党员中选3名,7名非党员中选3名的概率
所以.
故选:D
5.B
【解析】
【详解】
由题意得所求概率为.选.
6.B
【解析】
分析题意,根据互斥事件、对立事件的概率求解即可得到答案.
【详解】
由题意知,从袋中取出2个球的所有可能情况为:2个都是红球,2个都是黑球,1个红球和1个黑球.
由互斥事件的概率公式可得,取出的2个球中恰好一个红球一个黑球的概率是.
故选B.
【点睛】
求概率时首先要读懂题意,然后选择合适的概率类型求解.在解题时对于一些复杂事件的概率,可转化为若干个互斥事件的和事件的概率求解,属于基础题.
7.
【解析】
【分析】
根据个小矩形面积之和为1即可求出的值;根据频率分布直方图可以求出车速低于限速60 km/h的频率,从而可求出汽车有多少辆.
【详解】
由解得:.
这300辆汽车中车速低于限速60 km/h的汽车有.
故答案为:;.
8. ##
【解析】
【分析】
根据组合计数原理结合古典该型的概率公式可得出关于的等式,即可解得的值;从口袋中随机取出个球,设红色小球的个数为,可知随机变量的可能取值为、、、,求出随机变量在不同取值下的概率,进一步可求得的值.
【详解】
由已知可得,可得,解得,
从口袋中随机取出个球,设红色小球的个数为,则的可能取值为、、、,
则,,,,
因此,.
故答案为:;.
9.
【解析】
【分析】
结合超几何分布计算公式进行求解.
【详解】
由题意知的可能取值分别为0,1,2,3,且,
,,,
则.
故答案为:;
10.
【解析】
先由频率直方图得到60分以下的频率,再用对立事件的概率得到60分以上的频率.先通过频率直方图计算中的频率,再乘以样本容量得到人数.
【详解】
由频率直方图知,60分以下的频率为,
所以60分以上的频率为.
因为中的频率,
所以中的学生有.
故答案为:(1). (2).
【点睛】
本题主要考查样本估计总体中的频率直方图的应用,还考查了运算求解的能力,属于基础题.
11.
【解析】
【分析】
列出所有情况,统计满足条件的情况得到齐王每次胜利的概率,再根据独立事件计算得到答案.
【详解】
设齐王的上中下等马为,田忌的上中下等马为,
则共有9种情况,
其中齐王获胜的有6种情况,故,
.
故答案为:.
【点睛】
本题考查了概率的计算,意在考查学生的计算能力和应用能力.
12.0.9744
【解析】
【分析】
由题意知,本题符合独立重复试验条件,分情况讨论:若共有3人被治愈,若共有4人被治愈,分别代入独立重复试验公式得到结果.最后求和.
【详解】
解:由题意知本题分情况讨论:若共有3人被治愈,则;
若共有4人被治愈,则,
至少有3人被治愈概率.
故答案为:0.9477.
【点睛】
判断是否为独立重复试验的关键是每次试验事件的概率不变,并且每次试验的结果同其他各次试验的结果无关,重复是指试验为一系列的试验,并非一次试验,而是多次,但要注意重复事件发生的概率相互之间没有影响.
13.(1);(2)(i);(ii)159人.
【解析】
【分析】
(1)根据古典概型的概率计算公式,分别用列举法列举出选法总数以及两天相邻的选法数,即可算出;
(2)(i)利用最小二乘法计算出和,即可得出与的线性回归方程;
(ii)根据线性回归方程,令,即可预测第10天的痊愈人数.
【详解】
(1)选取的两天有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种选法,其中这两天相邻共(1,2),(2,3),(3,4),(4,5),所以概率为.
(2)(i)因为,,,,
所以,,
所以回归方程为.
(ii)当时,.
预测第10天的痊愈人数为159人.
【点睛】
本题主要考查古典概型的概率公式的应用,利用最小二乘法求线性回归方程,并利用线性回归方程进行预测,意在考查学生的数学运算能力,属于基础题.
14.(1);(2)分布列见解析,;(3).
【解析】
【分析】
(1)由独立事件同时发生的概率公式即可求解;
(2)可能的取值为,分别求出对应的概率,即可得分布列和数学期望;
(3)由独立事件同时发生的概率公式以及互斥事件的概率公式即可求解.
【详解】
(1)该同学所有题目都答对的概率为,
(2)由题意可得:可能的取值为,
,
,
所以X的分布列为:
,
(3)该同学总分为分得情况为:只答对或只答对,
所以该同学总分为3分的概率:.
15.(1)(2)
【解析】
【详解】
试题分析:(1)根据平均数公式得(2)先确定经济损失大于元且不超过元所对应的范围:由得.再对照表格确定天数,最后根据古典概型概率求法得结果
试题解析:(1)该城市这天空气质量指数的平均值为.
(2)设“在本月天中随机抽取一天,该天经济损失大于元且不超过元” 为事件
由得.根据表格数据得共有天, 所以.
考点:古典概型概率
【方法点睛】古典概型中基本事件数的探求方法
(1)列举法.
(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.
(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.
16.(1)1482;(2)分布列为见解析,数学期望为.
【解析】
【分析】
(1)根据正态分布的公式求得,再乘以总数即可得到结果;
(2)先求出概率,写出分布列,求出数学期望即可.
【详解】
(1)由题意得:,根据正态分布的公式得到:,
再乘以总数得到结果0.0228×65000=1482.
估计有1482位同学旅游费用支出在8100元以上
(2)Y的可能取值为0,1,2,3.
;
;
;
.
Y的分布列为:
Y 0 1 2 3
P
所以,Y的数学期望为:
.
17.(1)0.015;(2).
【解析】
【分析】
根据频率分布直方图中所有小矩形的面积之和等于1列出关于m的方程,解得.
由分层抽样可得成绩在区间的人数为3个,成绩在区间的人数为2个,列出所有抽取2人的情况,可以得到2人的成绩均在区间内只有1种情况,从而根据古典概型概率计算公式求得概率即可.
【详解】
解:依题意可知组距为10,
由,
解得 .
抽取了一个容量为5的样本成绩在区间的人数为: 人,
记3人为a、b、c.
成绩在区间的人数为:人,
记2人为d、e ,
任取2人的基本事件为:ab、ac、ad、ae、bc、bd、be、cd、ce、de,共计10个
其中在区间的基本事件为:de ,共计1个 ,
所以2人的成绩均在区间的概率为:.
【点睛】
有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.
18.(1)
(2)分布列见解析,2.5分
【解析】
【分析】
(1)根据相互独立事件的概率公式进行求解即可;
(2)根据相互独立事件的概率公式,结合数学期望公式进行求解判断即可.
(1)
因为甲同学三题得分合计为6分,所以这三道题每道题得2分,
所以甲同学三题得分合计为6分的概率为:
(2)
乙同学计划每题均随机选取两项,则三题每题可能得分为0分或5分
得5分的概率为,得0分的概率为
乙同学的三道题得分Y的可能取值为0,5,10,15
,
,
所以Y的分布列为:
0 5 10 15
因此分
19.(1);(2)分布列见解析,;(3)足够.
【解析】
【分析】
(1)本题可根据频率分布直方图求出样本平均数;
(2)本题首先可通过频率分布直方图求出“不健康生活方式者”和“超健康生活方式者”的人数,然后求出的所有可能的值以及对应的概率,即可列出的分布列,最后根据的分布列即可求出的数学期望;
(3)本题可通过频率分布直方图求出、内的人数,然后求出奖励所需要的总金额并与进行对比,即可得出结果.
【详解】
(1)由频率分布直方图易知,50名教职工日行步数的样本平均数为:
.
(2)由频率分布直方图易知,50名职工中“不健康生活方式者”和“超健康生活方式者”各有6人,
则的所有可能的值为、、、,
,,
,,
故的分布列为:
0 1 2 3
.
(3)用样本估计总体,步数在内的概率为,有人,
步数在内的概率为,有人,
因为,所以的预算足够.
20.(1)事件“认为作业不多”和事件“喜欢手机网游且认为作业多”的概率分别为、;
(2).
【解析】
【分析】
(1)利用古典概型的概率公式可求得所求事件的概率;
(2)确定所选的名学生中,“不喜欢手机网游”和“喜欢手机网游”的学生人数,加以标记,列举出所有的基本事件,确定所求事件所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率.
(1)
解:由题意可知,全班名学生中,“认为作业不多”的学生人数为人,
“喜欢手机网游且认为作业多”的学生人数为人,
因此,随机地抽问这个班的一名学生,事件“认为作业不多”的概率为,
事件“喜欢手机网游且认为作业多”的概率为.
(2)
解:在“认为作业多”的学生中已经用分层抽样的方法选取了名学生,
这名学生中“不喜欢手机网游”的学生人数为,记为,
名学生中“喜欢手机网游”的学生人数为,分别记为、、、,
从这名学生中任取名学生,所有的基本事件有:、、、、、、、、、,共种,
其中,事件“恰有名“不喜欢手机网游”的学生”包含的基本事件有:、、、,共种,
故所求概率为.
答案第1页,共2页
答案第1页,共2页
