人教A版(2019)选修第三册第七章易错疑难集训word版含答案
文档属性
| 名称 | 人教A版(2019)选修第三册第七章易错疑难集训word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 613.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览




文档简介
人教A版(2019) 选修第三册 第七章 易错疑难集训
一、单选题
1.一个袋中有4个白球和3个红球,从中任取2个,则随机变量可能为( )
A.所取球的个数
B.其中含红球的个数
C.所取白球与红球的总数
D.袋中球的总数
2.现有3道理科题和2道文科题共5道题,若不放回地依次抽取2道题,则在第1次抽到理科题的条件下,第2次抽到理科题的概率为( ).
A. B. C. D.
3.某次校园活动中,组织者给到场的前1000名同学分发编号的号码纸,每人一张,活动结束时公布获奖规则.获奖规则为:①号码的三位数字之和是7的倍数者可获得纪念品;②号码的三位数字全是奇数者可获得纪念品.已知某同学的号码满足获得纪念品的条件,则他同时可以获得纪念品的概率是
A.0.016 B.0.032 C.0.064 D.0.128
4.抛掷两枚骰子各一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数的差为X,则“X>4”表示试验的结果为( )
A.第一枚为5点,第二枚为1点
B.第一枚大于4点,第二枚也大于4点
C.第一枚为6点,第二枚为1点
D.第一枚为4点,第二枚为1点
二、填空题
5.甲 乙两队在一次对抗赛的某一轮中有3个抢答题,比赛规定:对于每一个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分),若是甲队在该轮比赛获胜时的得分(分数高者胜).则的所有可能取值之和是___________.
6.抛掷骰子2次,每次结果用表示,其中,分别表示第一次 第二次骰子朝上的点数.若设,,则______.
7.2021年6月14日是中国的传统节日“端午节”,这天人们会吃粽子、赛龙舟.现有七个粽子,其中三个是腊肉馅,四个是豆沙馅,小明随机取两个,记事件A为“取到的两个为同一种馅”,事件B为“取到的两个都是豆沙馅”,则______.
8.一用户在打电话时忘记了最后3个号码,只记得最后3个数两两不同,且都大于5.于是他随机拨最后3个数(两两不同),设他拨到正确号码的次数为X,随机变量X的可能值有_____个.
三、解答题
9.(1)某旅行社有导游9人,其中3人只会英语,4人只日语,其余2人既会英语,也会日语,现从中选6人,其中3人进行英语导游,另外3人进行日语导游,则不同的选择方法有多少种?
(2)一批零件共有100个,次品率为10%,每次从其中任取一个零件,取出的零件不再放回去:求第三次才取得合格格品的概率.
10.2021年,广东省将实施新高考,2018年暑期入学的高一学生是新高考首批考生,新高考不再分文理科,采用模式,其中“3”是指语文、数学、外语;“1”是指在物理和历史中必选一科(且只能选一科);“2”是指在化学,生物,政治,地理四科中任选两科.为积极推进新高考,某中学将选科分为两个环节,第一环节:学生在物理和历史两科中选择一科;第二环节:学生在化学,生物,政治,地理四科中任选两科.若一个学生两个环节的选科都确定,则称该学生的选考方案确定;否则,称该学生选考方案待确定.该学校为了解高一年级1000名学生选考科目的意向,随机选取50名学生进行了一次调查,这50人第一环节的选考科目都确定,有32人选物理,18人选历史;第二环节的选考科目已确定的有30人,待确定的有20人,具体调查结果如下表:
选考方案确定情况 化学 生物 政治 地理
物理 选考方案确定的有18人 16 11 5 4
选考方案待确定的有14人 5 5 0 0
历史 选考方案确定的有12人 3 5 4 12
选考方案待确定的有6人 0 0 3 2
(1)估计该学校高一年级选考方案确定的学生中选考政治的学生有多少人?
(2)从选考方案确定的12名历史选考生中随机选出2名学生,设随机变量,求的分布列及数学期望.
(3)在选考方案确定的18名物理选考生中,有11名学生选考方案为物理、化学、生物,试问剩余7人中选考方案为物理、政治、地理的人数.(只需写出结果)
11.甲、乙两位同学参加数学建模比赛.在备选的道题中,甲答对每道题的概率都是;乙能答对其中的道题.甲、乙两人都从备选的道题中随机抽出道题独立进行测试.规定至少答对题才能获奖.
(1)求甲同学在比赛中答对的题数的分布列和数学期望;
(2)求比赛中甲、乙两人至少有一人获奖的概率.
12.近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中.
(I)求的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从,中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在的概率.
13.某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同的取法有多少种?
(2)其中某一种假货不能在内,不同的取法有多少种?
(3)恰有2种假货在内,不同的取法有多少种?
(4)至少有2种假货在内,不同的取法有多少种?
(5)至多有2种假货在内,不同的取法有多少种?
14.幼儿园组织“选妈妈”游戏:有四位妈妈分别躲在四个外观一模一样的花轿里让小朋友们去猜哪一个花轿里是自已的妈妈.假设各位小朋友都是随机选择,选到每一位妈妈都是等可能的.
(1)已知妮妮的妈妈在某个花轿里,如果给妮妮两次机会单独去玩“选妈妈”游戏,求他选到自己妈妈的概率;
(2)如果四位妈妈所对应的四位小朋友一起选择,一人只选一个花轿,而且每个人选的花轿都不相同,记恰好选到自己妈妈的人数为,求的分布列与数学期望.
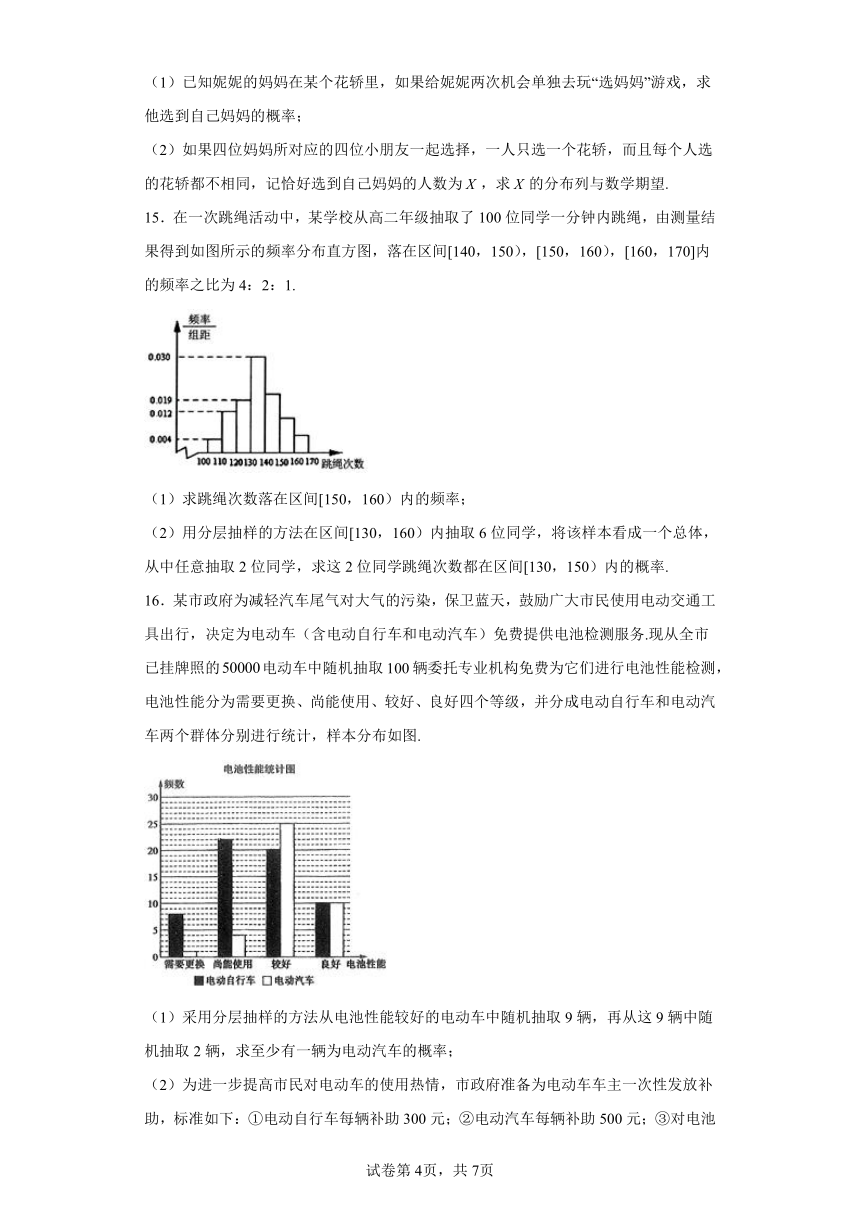
15.在一次跳绳活动中,某学校从高二年级抽取了100位同学一分钟内跳绳,由测量结果得到如图所示的频率分布直方图,落在区间[140,150),[150,160),[160,170]内的频率之比为4:2:1.
(1)求跳绳次数落在区间[150,160)内的频率;
(2)用分层抽样的方法在区间[130,160)内抽取6位同学,将该样本看成一个总体,从中任意抽取2位同学,求这2位同学跳绳次数都在区间[130,150)内的概率.
16.某市政府为减轻汽车尾气对大气的污染,保卫蓝天,鼓励广大市民使用电动交通工具出行,决定为电动车(含电动自行车和电动汽车)免费提供电池检测服务.现从全市已挂牌照的电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
(1)采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,再从这9辆中随机抽取2辆,求至少有一辆为电动汽车的概率;
(2)为进一步提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:①电动自行车每辆补助300元;②电动汽车每辆补助500元;③对电池需要更换的电动车每辆额外补助400元.试求抽取的100辆电动车执行此方案的预算;并利用样本估计总体,试估计市政府执行此方案的预算.
17.世界各国越来越关注环境保护问题,某检测点连续100天监视空气质量指数(AQI),将这100天的AQI数据分为五组,各组对应的区间为.并绘制出如图所示的不完整的频率分布直方图.
(1)请将频率分布直方图补充完整;
(2)已知空气质量指数AQI在内的空气质量等级为优,在内的空气质量等级为良,分别求这100天中空气质量等级为优与空气质量等级为良的天数;
(3)在(2)的条件下,在空气质量等级为优和良的天数中,先按分层抽样的方法已经选定了6天,然后再从这6天中任取两天,求这两天的空气质量等级相同的概率.
18.甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲、丙两台机床加工的零件都是一等品的概率为.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
19.如图,从左到右有5个空格.
(1)若向这5个格子填入0,1,2,3,4五个数,要求每个数都要用到,且第三个格子不能填0,则一共有多少不同的填法?
(2)若给这5个空格涂上颜色,要求相邻格子不同色,现有红黄蓝3颜色可供使用,问一共有多少不同的涂法?
(3)若向这5个格子放入7个不同的小球,要求每个格子里都有球,问有多少种不同的放法?
20.某大学就业部从该校2018年毕业的且已就业的大学本科生中随机抽取100人进行问卷调查,其中有一项是他们的月薪情况.经调查发现,他们的月薪在3000元到10000元之间,根据统计数据得到如下频率分布直方图:
若月薪在区间的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科生就业提供更好的指导意见.其中,分别为样本平均数和样本标准差计,计算可得元(同一组中的数据用该区间的中点值代表).
(1)现该校2018届大学本科生毕业生张铭的月薪为3600元,试判断张铭是否属于“就业不理想”的学生?
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽取6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5000 元的概率.
21.“让几千万农村贫困人口生活好起来,是我心中的牵挂.”习近平总书记多次对精准扶贫、精准脱贫作出重要指示,某大学生村干部为帮助某扶贫户脱贫,帮助其种植某品种金桔,并利用互联网进行网络销售,为了更好销售,现从金桔树上随机摘下100个果实进行测重,每个金桔质量分布在区间(单位:克),并且依据质量数据作出其频率分布直方图,如图所示:
(1)按分层抽样的方法从质量落在,的金桔中随机抽取5个,再从这5个金桔中随机抽2个,求这2个金桔质量至少有一个不小于40克的概率;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率.根据经验,该户的金桔种植地上大约有100000个金桔待出售,某电商提出两种收购方案:
方案:所有金桔均以4元/千克收购;
方案:低于40克的金桔以2元/千克收购,其余的以5元/千克收购;
请你通过计算为该户选择收益较好的方案.
22.在2019年女排世界杯中,中国女子排球队以11连胜的优异战绩成功夺冠,为祖国母亲七十华诞献上了一份厚礼,排球比赛采用5局3胜制,前4局比赛采用25分制,每个队只有赢得至少25分,并同时超过对方2分时,才胜1局;在决胜局(第五局)采用15分制,每个队只有赢得至少15分,并领先对方2分为胜,在每局比赛中,发球方赢得此球后可得1分,并获得下一球的发球权,否则交换发球权,并且对方得1分,现有甲、乙两队进行排球比赛:
(1)若前三局比赛中甲已经赢两局,乙赢一局,接下来两队赢得每局比赛的概率均为,求甲队最后赢得整场比赛的概率;
(2)若前四局比赛中甲、乙两队已经各赢两局比赛,在决胜局(第五局)中,两队当前的得分为甲、乙各14分,且甲已获得下一发球权,若甲发球时甲赢1分的概率为,乙发球时甲赢1分的概率为,得分者获得下一个球的发球权,设两队打了个球后甲赢得了整场比赛,求的值及相应的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据离散型随机变量的定义逐一判断四个选项的正误,即可得正确选项.
【详解】
对于A:所取球的个数为2个,是定值,故不是随机变量,故选项A不正确;
对于B:从中任取2个其中含红球的个数为是随机变量,故选项B正确;
对于C:所取白球与红球的总数为2个,是定值,故不是随机变量,故选项C不正确;
对于D:袋中球的总数为7个,是定值,故不是随机变量,故选项D不正确;
故选:B.
2.D
【解析】
【分析】
设第1次抽到理科题的事件为A,第2次抽到理科题的事件为B,分别求得 ,代入公式求解.
【详解】
设第1次抽到理科题的事件为A,第2次抽到理科题的事件为B,
所以 ,
所以第1次抽到理科题的条件下,第2次抽到理科题的概率为,
故选:D
【点睛】
本题主要考查条件概率的求法,还考查了运算求解的能力,属于基础题.
3.D
【解析】
【分析】
记某同学获得纪念品 纪念品分別为事件 ,由分步乘法计数原理结合古典概型概率公式可得;再由分类加法、排列组合的知识结合古典概型概率公式可得;最后由条件概率公式即可得解.
【详解】
记某同学获得纪念品 纪念品分別为事件 ,
则事件发生的充要条件是:三位数字均是1,3,5,7,9五个数中的一个,
对应的概率;
事件是在三位数字均为奇数的基础上,还需满足三位数字之和为7的倍数,
三个之间的数字之和范围为,
又因为每位数字都是奇数,故其和亦为奇数,
故三位数字之和只可能是7或21,所以三位数字从小到大排列只有以下五种可能:
①1,1,5,对应的三位数个数为;
②1,3,3,对应的三位数个数为;
③3,9,9,对应的三位数个数为;
④5,7,9,对应的三位数个数为;
⑤7,7,7,对应的三位数有1个;
故.
于是所求概率为.
故选:D.
【点睛】
本题考查了计数原理及古典概型概率公式的应用,考查了条件概率公式的应用及运算求解能力,属于中档题.
4.C
【解析】
【分析】
由随机变量的可能取值求解.
【详解】
抛掷两枚骰子各一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数的差为X,
所以“X>4”即“X=5”,
表示试验的结果为第一枚为6点,第二枚为1点,
故选:C
5.5
【解析】
【分析】
列举所有获胜的情况,得到的取值,即可求值.
【详解】
X= 1,甲抢到一题但答错了,而乙抢到了两个题目都答错了,
X=0,甲没抢到题,乙抢到题目答错至少2个题或甲抢到2题,但答时一对一错,而乙答错一个题目.
X=1,甲抢到1题且答对,或甲抢到3题,且1错2对.
X=2,甲抢到2题均答对.
X=3,甲抢到3题均答对.
所以的所有可能取值,和为5.
故答案为:
6.
【解析】
【分析】
利用条件概率的公式直接求解即可
【详解】
因为抛掷骰子2次共有36种情况,其中和为10的有(4,6),(5,5),(6,4)三种情况,当和为10时,的有1种,
所以,,
所以.
故答案为:
7.
【解析】
【分析】
根据题意,结合条件概率的计算公式,即可求解.
【详解】
由题意,可知.
故答案为:.
8.
【解析】
【分析】
大于的数是,利用排列数计算出随机拨打的所有可能,由此得出所有可能取值的个数.
【详解】
大于的数是,一共有个,从中取出不同的三个进行排列,方法数有种.
【点睛】
本小题主要考查对离散型随机变量的理解,考查排列问题的识别以及排列数的计算,考查分析和解决问题的能力,属于基础题.题目关键点有两点,一个是记得的数都大于,这样的话可以确定出拨打的数为中的三个.由于电话号码是有顺序的差别的,故是排列问题,需要用排列数来计算出方法数.
9.(1);(2).
【解析】
(1)通过分类的方式,求得每一类别的情况,最后利用分类加法计数原理求解即可;(2)
分别计算出第一次,第二次取次品的概率和第三次取合格品的概率,第三次取合格品的概率为三者之积.
【详解】
(1)若只会英语的人中选了人作英语导游,共有种情况;
若只会英语的人中选了人作英语导游,共有种情况;
若只会英语的人中选了人作英语导游,共有种情况;
由分类加法计数原理可得,共有:种情况,
综上:不同的选择方法有种;
(2)由题意知:
次品总数为个,合格品总数为个,
第一次取的一定是次品,概率为;
第二次取的一定是次品,概率为;
第三次取的一定是合格品,概率为;
所以第三次才取得合格格品的概率为.
综上:第三次才取得合格格品的概率为.
【点睛】
本题主要考查了排列组合,考查了分类加法计数原理和分步乘法计数原理.属于中档题.
10.(1)180;(2);(3)2人.
【解析】
【分析】
(1)利用分层抽样原理求得对应的学生人数;(2)由题意知随机变量的可能取值,计算对应的概率,写出的分布列,计算数学期望值;(3)由化学中去除11人后余5人,结合选政治和地理的人数,可得所求.
【详解】
(1)由数据可知,选考方案确定的18名物理选考生中确定选考政治的有5人,选考方案确定的12名历史选考生中确定选考政治的有4人
所以,估计该学校高一年级选考方案确定的学生中选考政治的学生有人
(2)由数据可知,选考方案确定的12名历史考生中有3人选考化学、地理;有5人选考生物、地理;有4人选考政治、地理.
由已知得的所有取值为0,1,则
所以的分布列为
0 1
所以数学期望.
(3)剩余7人中选考方案为物理、政治、地理的人数为2.
【点睛】
本题考查了分层抽样的计算,也考查了离散型随机变量的分布列与数学期望问题,是中档题.
11.(1)分布列答案见解析,数学期望为;(2).
【解析】
【分析】
(1)分析可知,利用二项分布可得出随机变量的分布列以及的值;
(2)计算出甲、乙分别获奖的概率,再利用独立事件和对立事件的概率公式可求得所求事件的概率.
【详解】
(1)由题意可知,
,,
,,
,
所以的分布列如下:
所以,;
(2)记“甲获奖”为事件,设乙答对的题数为,“乙获奖”为事件.
;
.
记“甲、乙至少有一人获奖”为事件,则为“甲、乙两人都未获奖”.
.
答:甲、乙至少有一人获奖的概率为.
12.(Ⅰ)(Ⅱ) 平均数74.9,众数75.14,中位数75;(Ⅲ)
【解析】
【分析】
(I)根据频率之和为列方程,结合求出的值.(II)利用各组中点值乘以频率然后相加,求得平均数.利用中位数是面积之和为的地方,列式求得中位数.以频率分布直方图最高一组的中点作为中位数.(III)先计算出从,中分别抽取人和人,再利用列举法和古典概型概率计算公式,计算出所求的概率.
【详解】
解:(I)依题意得,所以,
又,所以.
(Ⅱ)平均数为
中位数为
众数为
(Ⅲ)依题意,知分数在的市民抽取了2人,记为,分数在的市民抽取了6人,记为1,2,3,4,5,6,
所以从这8人中随机抽取2人所有的情况为:
,
共28种,
其中满足条件的为,共13种,设“至少有1人的分数在”的事件为,则
【点睛】
本小题主要考查求解频率分布直方图上的未知数,考查利用频率分布直方图估计平均数、中位数和众数的方法,考查利用古典概型求概率.属于中档题.
13.(1)561;(2)5984;(3)2100;(4)2555;(5)6090.
【解析】
(1)从余下的34种商品中,任选取2种,问题得以解决.
(2)从余下的34种可选商品中,任选取3种,问题得以解决.
(3)从20种真货中选取1件,从15种假货中选取2件,问题得以解决.
(4)分选取2种假货,选取3种假货两种情况,问题得以解决.
(5)选取3种的总数减去选取3种假货得情况,问题得以解决.
【详解】
解:(1)从余下的34种商品中,选取2种有 (种),
∴某一种假货必须在内的不同取法有561种.
(2)从余下的34种可选商品中,选取3种,有(种).
∴某一种假货不能在内的不同取法有5 984种.
(3)从20种真货中选取1件,从15种假货中选取2件有(种).
∴恰有2种假货在内的不同的取法有2 100种.
(4)选取2种假货有种,选取3种假货种,共有选取方式 (种).
∴至少有2种假货在内的不同的取法有2 555种.
(5)选取3种的总数为,选取3种假货有种,因此共有选取方式 (种).
∴至多有2种假货在内的不同的取法有6 090种.
【点睛】
本题主要考察了排列、组合及简单计数问题,考查学生分析解决问题的能力,属于中档题.
14.(1);(2)分布列答案见解析,数学期望:.
【解析】
【分析】
(1)若妮妮第一次就选到自己妈妈的概率为,若妮妮第一次没有选到自己妈妈,第二次选到自己妈妈的概率为,然后可得答案.
(2)由题意知的所有可能值为 ,分别求出其概率,列出分布列,由公式求出期望.
【详解】
(1)记“妮妮选到自己妈妈”为事件,则;
(2)由题意知的所有可能值为 ,
则, ,
, ,
∴随机变量的分布列:
则.
15.(1)0.10;(2)
【解析】
【分析】
(1)由图中小矩形的面积之和为1可得[140,170)的频率,再由频率之比即得;(2)先确定[140,150),[150,160),[160,170]三个区间的频率,再分层抽样,最后根据古典概型求出概率。
【详解】
(1)∵图中小矩形的面积之和为1,
∴[140,170)的频率为:1﹣(0.04+0.12+0.19+0.30)=0.35,
∵[140,150),[150,160),[160,170)的频率之比为4:2:1,
∴[150,160)的频率为0.10,
(2)∵区间[140,150)的频率为0.20,
∴[130,140),[140,150),[150,160)内的频率依次为0.30,0.20,0.10,
用分层抽样的方法在区间[130,160)内抽取一个容量为6的样本,
则在区间[130,140)内应抽取63,设为A1,A2,A3,
在区间[140,150)内应抽取62,记为B1,B2,
在区间[150,160)内应抽取61,记为C,
设“从样本中任意抽取2位同学,这2位同学都在区间[130,150)内”这事件M,
则所有的基本事件有15个,分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),
(A2,C),(A3,B1),(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),
事件M包含的基本事件有10种,分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),
∴这2位同学跳绳次数都在区间[130,150)内的概率P(M).
【点睛】
本题考查根据频率分布直方图求区间频率,以及分层抽样和古典概型,是常考题型。
16.(1);(2).
【解析】
【分析】
(1)根据频数图,利用分层抽样得电动自行车应抽取4辆,电动汽车应抽取5辆,再利用古典概型和对立事件求得:至少有一辆为电动汽车的概率为;
(2)由频数图,计算样本中100辆电动车共补助元,算出每辆电动车平均需补助的钱乘以可得估计出市政府执行此方案的预算.
【详解】
(1)根据分层抽样的原理,电动自行车应抽取(辆),
电动汽车应抽取(辆).
从9辆电动车中抽取2辆,设电动汽车和电动自行车分别为,,,,,,,,,
可得抽法总数为36种,
其中2辆均为电动自行车的有,,,,,,共6种.
“设从这9辆中随机抽取2辆,至少有一辆为电动汽车”为事件,
则.
(2)由条件可知,这100辆电动车中电动自行车60辆,电动汽车40辆,其中电池需要更换的电动自行车8辆,电动汽车1辆.根据补助方案可知,这100辆电动车共补助
(元).
由样本估计总体,市政府执行此方案的预算大约需要
(元).即为所求.
【点睛】
本题考查从图中抽取数据信息、古典概型计算概率、样本估计总体思想,考查基本数据处理能力.
17.(1)直方图见解析;(2)40;(3).
【解析】
(1)先求出在,内的频率,从而在,内的,由此能把频率分布直方图补充完整.
(2)这100天中空气质量等级为优的天数为,空气质量等级为良的天数为,
(3)选定的6天中有2天空气质量等级为优,有4天为良分别记为,和,,,,记事件“从这6天中任取两天,这两天的空气质量等级相同”为,利用列举法能坟出这两天的空气质量等级相同的概率.
【详解】
解:(1)因为AQI在内的频率为
所以AQI在内的
故频率分布直方图补充完整如图所示.
(2)这100天中空气质量等级为优的天数为
空气质量等级为良的天数为
(3)由(2)可知,选定的6天中有2天空气质量等级为优,有4天为良
分别记为和
记事件“从这6天中任取两天,这两天的空气质量等级相同”为M,
则事件M包含的基本事件有
共有7个基本事件
而从6天中任取两天包含的基本事件有
共有15个基本事件,
∴从这6天中任取两天,这两天的空气质量等级相同的概率
【点睛】
本题考查频率分布直方图的画法、频数、概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.
18.(1),,;(2)
【解析】
【分析】
(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,则再利用独立事件的概率计算公式,解方程组即可得到答案.
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,利用对立事件,即计算即可.
【详解】
(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,
由题设条件有即
解得,,.
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别是,,;
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,则
.
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为.
【点晴】
本题主要考查独立事件的概率计算问题,涉及到对立事件的概率计算,考查学生的数学运算能力,是一道容易题.
19.(1);(2);(3)
【解析】
【分析】
(1)直接利用排除法计算得到答案.
(2)根据乘法原理计算得到答案.
(3)将情况分为的组和的组,计算得到答案.
【详解】
(1)利用排除法:种.
(2)根据乘法原理得到:共有种涂法.
(3)若分成的组,则共有种分法;
若分成的组,则共有种分法,
故共有种放法.
【点睛】
本题考查了排列组合的应用,意在考查学生的计算能力和应用能力.
20.(1)属于;(2).
【解析】
(1)由频率分布直方图求出,从而得到具体的,即可判断.
(2)结合分层抽样的知识点首先求出前三组各抽多少人,然后结合排列组合的思想求出从6人中抽取2人的组合数以及恰有一人月薪不超过5000 元的组合数,最后由古典概型概率公式即可求出.
【详解】
(1)解: 由频率分布直方图知
则.在的左侧,
所以张铭属于“就业不理想”的学生.
(2)解:前三组频率之比为
所以抽取的6人中,第一组有1人,第二组有2人,第三组有3人.
从6人中再抽2人的组合数为种. 其中,恰有一人月薪不超过5000 元的组合数为
种.设”恰有1人月薪不超过5000 元”.则
所以获赠智能手机的2人中恰有1人月薪不超过5000 元的概率为.
【点睛】
本题考查了由频率分布直方图估计样本平均数,考查了古典概型,考查了分层抽样,考查了排列组合.本题的难点在于计算.易错点是记错求平均数公式,误用每个长方形的高与其横坐标中点相乘.
21.(1);(2)选方案好.
【解析】
(1)根据分层抽样找出金桔个数,然后找出所有事件,以及满足题目要求的事件,套用古典概型的概率公式,即可得到本题答案.
(2)根据两个不同的方案,计算出收益,判断最优方案.
【详解】
解:(1)由题,得金桔质量在和的比例为,
所以从质量落在,的金桔中分别取2个和3个,
记金桔中取的2个设为,金桔中取的3个设为,
有,共10个事件,
满足题目要求的有,,共9个事件,
所以2个金桔质量至少有一个不小于40克的概率为;
(2)方案好,理由如下:
由频率直方图可知:金桔质量在各个区间的频率依次为0.1,0.2,0.3,0.25,0.15.
各个区间的金桔个数为:10000,20000,30000,25000,15000,
若按方案销售:;
若按方案销售:
低于40克的金桔有个,不低于40克的金桔有70000个,
总收益有,
故选方案好.
【点睛】
本题主要考查频率直方图的应用,分层抽样以及古典概型的求法,考查学生分析问题和解决问题的能力,以及运算求解能力.
22.(1);(2)答案见详解.
【解析】
【分析】
(1)甲队最后赢得整场比赛的情况为第四局赢或第四局输第五局赢,算出答案即可.
(2)的取值只能为2,4或6,对应比分为,,,分别分析对应的情况,求出对应的概率即可.
【详解】
(1)甲队最后赢得整场比赛的情况为第四局赢或第四局输第五局赢,
所以甲队最后赢得整场比赛的概率为.
(2)根据比赛规则,的取值只能为2,4或6,对应比分为,,.
两队打了2个球后甲赢得整场比赛,即打第一个球甲发球甲得分,
打第二个球甲发球甲得分,此时概率为;
两队打了4个球后甲赢得整场比赛,即打第一个球甲发球甲得分,打第二个球甲发球甲失分,
打第三个球乙球甲发球甲得分,打第四个球甲发球甲得分,此时概率为.
两队打了6个球后甲赢得整场比赛,6个球的胜负情况如图(胜者用√表示),
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
答案第1页,共2页
答案第1页,共2页
一、单选题
1.一个袋中有4个白球和3个红球,从中任取2个,则随机变量可能为( )
A.所取球的个数
B.其中含红球的个数
C.所取白球与红球的总数
D.袋中球的总数
2.现有3道理科题和2道文科题共5道题,若不放回地依次抽取2道题,则在第1次抽到理科题的条件下,第2次抽到理科题的概率为( ).
A. B. C. D.
3.某次校园活动中,组织者给到场的前1000名同学分发编号的号码纸,每人一张,活动结束时公布获奖规则.获奖规则为:①号码的三位数字之和是7的倍数者可获得纪念品;②号码的三位数字全是奇数者可获得纪念品.已知某同学的号码满足获得纪念品的条件,则他同时可以获得纪念品的概率是
A.0.016 B.0.032 C.0.064 D.0.128
4.抛掷两枚骰子各一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数的差为X,则“X>4”表示试验的结果为( )
A.第一枚为5点,第二枚为1点
B.第一枚大于4点,第二枚也大于4点
C.第一枚为6点,第二枚为1点
D.第一枚为4点,第二枚为1点
二、填空题
5.甲 乙两队在一次对抗赛的某一轮中有3个抢答题,比赛规定:对于每一个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分),若是甲队在该轮比赛获胜时的得分(分数高者胜).则的所有可能取值之和是___________.
6.抛掷骰子2次,每次结果用表示,其中,分别表示第一次 第二次骰子朝上的点数.若设,,则______.
7.2021年6月14日是中国的传统节日“端午节”,这天人们会吃粽子、赛龙舟.现有七个粽子,其中三个是腊肉馅,四个是豆沙馅,小明随机取两个,记事件A为“取到的两个为同一种馅”,事件B为“取到的两个都是豆沙馅”,则______.
8.一用户在打电话时忘记了最后3个号码,只记得最后3个数两两不同,且都大于5.于是他随机拨最后3个数(两两不同),设他拨到正确号码的次数为X,随机变量X的可能值有_____个.
三、解答题
9.(1)某旅行社有导游9人,其中3人只会英语,4人只日语,其余2人既会英语,也会日语,现从中选6人,其中3人进行英语导游,另外3人进行日语导游,则不同的选择方法有多少种?
(2)一批零件共有100个,次品率为10%,每次从其中任取一个零件,取出的零件不再放回去:求第三次才取得合格格品的概率.
10.2021年,广东省将实施新高考,2018年暑期入学的高一学生是新高考首批考生,新高考不再分文理科,采用模式,其中“3”是指语文、数学、外语;“1”是指在物理和历史中必选一科(且只能选一科);“2”是指在化学,生物,政治,地理四科中任选两科.为积极推进新高考,某中学将选科分为两个环节,第一环节:学生在物理和历史两科中选择一科;第二环节:学生在化学,生物,政治,地理四科中任选两科.若一个学生两个环节的选科都确定,则称该学生的选考方案确定;否则,称该学生选考方案待确定.该学校为了解高一年级1000名学生选考科目的意向,随机选取50名学生进行了一次调查,这50人第一环节的选考科目都确定,有32人选物理,18人选历史;第二环节的选考科目已确定的有30人,待确定的有20人,具体调查结果如下表:
选考方案确定情况 化学 生物 政治 地理
物理 选考方案确定的有18人 16 11 5 4
选考方案待确定的有14人 5 5 0 0
历史 选考方案确定的有12人 3 5 4 12
选考方案待确定的有6人 0 0 3 2
(1)估计该学校高一年级选考方案确定的学生中选考政治的学生有多少人?
(2)从选考方案确定的12名历史选考生中随机选出2名学生,设随机变量,求的分布列及数学期望.
(3)在选考方案确定的18名物理选考生中,有11名学生选考方案为物理、化学、生物,试问剩余7人中选考方案为物理、政治、地理的人数.(只需写出结果)
11.甲、乙两位同学参加数学建模比赛.在备选的道题中,甲答对每道题的概率都是;乙能答对其中的道题.甲、乙两人都从备选的道题中随机抽出道题独立进行测试.规定至少答对题才能获奖.
(1)求甲同学在比赛中答对的题数的分布列和数学期望;
(2)求比赛中甲、乙两人至少有一人获奖的概率.
12.近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中.
(I)求的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从,中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在的概率.
13.某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同的取法有多少种?
(2)其中某一种假货不能在内,不同的取法有多少种?
(3)恰有2种假货在内,不同的取法有多少种?
(4)至少有2种假货在内,不同的取法有多少种?
(5)至多有2种假货在内,不同的取法有多少种?
14.幼儿园组织“选妈妈”游戏:有四位妈妈分别躲在四个外观一模一样的花轿里让小朋友们去猜哪一个花轿里是自已的妈妈.假设各位小朋友都是随机选择,选到每一位妈妈都是等可能的.
(1)已知妮妮的妈妈在某个花轿里,如果给妮妮两次机会单独去玩“选妈妈”游戏,求他选到自己妈妈的概率;
(2)如果四位妈妈所对应的四位小朋友一起选择,一人只选一个花轿,而且每个人选的花轿都不相同,记恰好选到自己妈妈的人数为,求的分布列与数学期望.
15.在一次跳绳活动中,某学校从高二年级抽取了100位同学一分钟内跳绳,由测量结果得到如图所示的频率分布直方图,落在区间[140,150),[150,160),[160,170]内的频率之比为4:2:1.
(1)求跳绳次数落在区间[150,160)内的频率;
(2)用分层抽样的方法在区间[130,160)内抽取6位同学,将该样本看成一个总体,从中任意抽取2位同学,求这2位同学跳绳次数都在区间[130,150)内的概率.
16.某市政府为减轻汽车尾气对大气的污染,保卫蓝天,鼓励广大市民使用电动交通工具出行,决定为电动车(含电动自行车和电动汽车)免费提供电池检测服务.现从全市已挂牌照的电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
(1)采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,再从这9辆中随机抽取2辆,求至少有一辆为电动汽车的概率;
(2)为进一步提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:①电动自行车每辆补助300元;②电动汽车每辆补助500元;③对电池需要更换的电动车每辆额外补助400元.试求抽取的100辆电动车执行此方案的预算;并利用样本估计总体,试估计市政府执行此方案的预算.
17.世界各国越来越关注环境保护问题,某检测点连续100天监视空气质量指数(AQI),将这100天的AQI数据分为五组,各组对应的区间为.并绘制出如图所示的不完整的频率分布直方图.
(1)请将频率分布直方图补充完整;
(2)已知空气质量指数AQI在内的空气质量等级为优,在内的空气质量等级为良,分别求这100天中空气质量等级为优与空气质量等级为良的天数;
(3)在(2)的条件下,在空气质量等级为优和良的天数中,先按分层抽样的方法已经选定了6天,然后再从这6天中任取两天,求这两天的空气质量等级相同的概率.
18.甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲、丙两台机床加工的零件都是一等品的概率为.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
19.如图,从左到右有5个空格.
(1)若向这5个格子填入0,1,2,3,4五个数,要求每个数都要用到,且第三个格子不能填0,则一共有多少不同的填法?
(2)若给这5个空格涂上颜色,要求相邻格子不同色,现有红黄蓝3颜色可供使用,问一共有多少不同的涂法?
(3)若向这5个格子放入7个不同的小球,要求每个格子里都有球,问有多少种不同的放法?
20.某大学就业部从该校2018年毕业的且已就业的大学本科生中随机抽取100人进行问卷调查,其中有一项是他们的月薪情况.经调查发现,他们的月薪在3000元到10000元之间,根据统计数据得到如下频率分布直方图:
若月薪在区间的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科生就业提供更好的指导意见.其中,分别为样本平均数和样本标准差计,计算可得元(同一组中的数据用该区间的中点值代表).
(1)现该校2018届大学本科生毕业生张铭的月薪为3600元,试判断张铭是否属于“就业不理想”的学生?
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽取6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5000 元的概率.
21.“让几千万农村贫困人口生活好起来,是我心中的牵挂.”习近平总书记多次对精准扶贫、精准脱贫作出重要指示,某大学生村干部为帮助某扶贫户脱贫,帮助其种植某品种金桔,并利用互联网进行网络销售,为了更好销售,现从金桔树上随机摘下100个果实进行测重,每个金桔质量分布在区间(单位:克),并且依据质量数据作出其频率分布直方图,如图所示:
(1)按分层抽样的方法从质量落在,的金桔中随机抽取5个,再从这5个金桔中随机抽2个,求这2个金桔质量至少有一个不小于40克的概率;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率.根据经验,该户的金桔种植地上大约有100000个金桔待出售,某电商提出两种收购方案:
方案:所有金桔均以4元/千克收购;
方案:低于40克的金桔以2元/千克收购,其余的以5元/千克收购;
请你通过计算为该户选择收益较好的方案.
22.在2019年女排世界杯中,中国女子排球队以11连胜的优异战绩成功夺冠,为祖国母亲七十华诞献上了一份厚礼,排球比赛采用5局3胜制,前4局比赛采用25分制,每个队只有赢得至少25分,并同时超过对方2分时,才胜1局;在决胜局(第五局)采用15分制,每个队只有赢得至少15分,并领先对方2分为胜,在每局比赛中,发球方赢得此球后可得1分,并获得下一球的发球权,否则交换发球权,并且对方得1分,现有甲、乙两队进行排球比赛:
(1)若前三局比赛中甲已经赢两局,乙赢一局,接下来两队赢得每局比赛的概率均为,求甲队最后赢得整场比赛的概率;
(2)若前四局比赛中甲、乙两队已经各赢两局比赛,在决胜局(第五局)中,两队当前的得分为甲、乙各14分,且甲已获得下一发球权,若甲发球时甲赢1分的概率为,乙发球时甲赢1分的概率为,得分者获得下一个球的发球权,设两队打了个球后甲赢得了整场比赛,求的值及相应的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据离散型随机变量的定义逐一判断四个选项的正误,即可得正确选项.
【详解】
对于A:所取球的个数为2个,是定值,故不是随机变量,故选项A不正确;
对于B:从中任取2个其中含红球的个数为是随机变量,故选项B正确;
对于C:所取白球与红球的总数为2个,是定值,故不是随机变量,故选项C不正确;
对于D:袋中球的总数为7个,是定值,故不是随机变量,故选项D不正确;
故选:B.
2.D
【解析】
【分析】
设第1次抽到理科题的事件为A,第2次抽到理科题的事件为B,分别求得 ,代入公式求解.
【详解】
设第1次抽到理科题的事件为A,第2次抽到理科题的事件为B,
所以 ,
所以第1次抽到理科题的条件下,第2次抽到理科题的概率为,
故选:D
【点睛】
本题主要考查条件概率的求法,还考查了运算求解的能力,属于基础题.
3.D
【解析】
【分析】
记某同学获得纪念品 纪念品分別为事件 ,由分步乘法计数原理结合古典概型概率公式可得;再由分类加法、排列组合的知识结合古典概型概率公式可得;最后由条件概率公式即可得解.
【详解】
记某同学获得纪念品 纪念品分別为事件 ,
则事件发生的充要条件是:三位数字均是1,3,5,7,9五个数中的一个,
对应的概率;
事件是在三位数字均为奇数的基础上,还需满足三位数字之和为7的倍数,
三个之间的数字之和范围为,
又因为每位数字都是奇数,故其和亦为奇数,
故三位数字之和只可能是7或21,所以三位数字从小到大排列只有以下五种可能:
①1,1,5,对应的三位数个数为;
②1,3,3,对应的三位数个数为;
③3,9,9,对应的三位数个数为;
④5,7,9,对应的三位数个数为;
⑤7,7,7,对应的三位数有1个;
故.
于是所求概率为.
故选:D.
【点睛】
本题考查了计数原理及古典概型概率公式的应用,考查了条件概率公式的应用及运算求解能力,属于中档题.
4.C
【解析】
【分析】
由随机变量的可能取值求解.
【详解】
抛掷两枚骰子各一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数的差为X,
所以“X>4”即“X=5”,
表示试验的结果为第一枚为6点,第二枚为1点,
故选:C
5.5
【解析】
【分析】
列举所有获胜的情况,得到的取值,即可求值.
【详解】
X= 1,甲抢到一题但答错了,而乙抢到了两个题目都答错了,
X=0,甲没抢到题,乙抢到题目答错至少2个题或甲抢到2题,但答时一对一错,而乙答错一个题目.
X=1,甲抢到1题且答对,或甲抢到3题,且1错2对.
X=2,甲抢到2题均答对.
X=3,甲抢到3题均答对.
所以的所有可能取值,和为5.
故答案为:
6.
【解析】
【分析】
利用条件概率的公式直接求解即可
【详解】
因为抛掷骰子2次共有36种情况,其中和为10的有(4,6),(5,5),(6,4)三种情况,当和为10时,的有1种,
所以,,
所以.
故答案为:
7.
【解析】
【分析】
根据题意,结合条件概率的计算公式,即可求解.
【详解】
由题意,可知.
故答案为:.
8.
【解析】
【分析】
大于的数是,利用排列数计算出随机拨打的所有可能,由此得出所有可能取值的个数.
【详解】
大于的数是,一共有个,从中取出不同的三个进行排列,方法数有种.
【点睛】
本小题主要考查对离散型随机变量的理解,考查排列问题的识别以及排列数的计算,考查分析和解决问题的能力,属于基础题.题目关键点有两点,一个是记得的数都大于,这样的话可以确定出拨打的数为中的三个.由于电话号码是有顺序的差别的,故是排列问题,需要用排列数来计算出方法数.
9.(1);(2).
【解析】
(1)通过分类的方式,求得每一类别的情况,最后利用分类加法计数原理求解即可;(2)
分别计算出第一次,第二次取次品的概率和第三次取合格品的概率,第三次取合格品的概率为三者之积.
【详解】
(1)若只会英语的人中选了人作英语导游,共有种情况;
若只会英语的人中选了人作英语导游,共有种情况;
若只会英语的人中选了人作英语导游,共有种情况;
由分类加法计数原理可得,共有:种情况,
综上:不同的选择方法有种;
(2)由题意知:
次品总数为个,合格品总数为个,
第一次取的一定是次品,概率为;
第二次取的一定是次品,概率为;
第三次取的一定是合格品,概率为;
所以第三次才取得合格格品的概率为.
综上:第三次才取得合格格品的概率为.
【点睛】
本题主要考查了排列组合,考查了分类加法计数原理和分步乘法计数原理.属于中档题.
10.(1)180;(2);(3)2人.
【解析】
【分析】
(1)利用分层抽样原理求得对应的学生人数;(2)由题意知随机变量的可能取值,计算对应的概率,写出的分布列,计算数学期望值;(3)由化学中去除11人后余5人,结合选政治和地理的人数,可得所求.
【详解】
(1)由数据可知,选考方案确定的18名物理选考生中确定选考政治的有5人,选考方案确定的12名历史选考生中确定选考政治的有4人
所以,估计该学校高一年级选考方案确定的学生中选考政治的学生有人
(2)由数据可知,选考方案确定的12名历史考生中有3人选考化学、地理;有5人选考生物、地理;有4人选考政治、地理.
由已知得的所有取值为0,1,则
所以的分布列为
0 1
所以数学期望.
(3)剩余7人中选考方案为物理、政治、地理的人数为2.
【点睛】
本题考查了分层抽样的计算,也考查了离散型随机变量的分布列与数学期望问题,是中档题.
11.(1)分布列答案见解析,数学期望为;(2).
【解析】
【分析】
(1)分析可知,利用二项分布可得出随机变量的分布列以及的值;
(2)计算出甲、乙分别获奖的概率,再利用独立事件和对立事件的概率公式可求得所求事件的概率.
【详解】
(1)由题意可知,
,,
,,
,
所以的分布列如下:
所以,;
(2)记“甲获奖”为事件,设乙答对的题数为,“乙获奖”为事件.
;
.
记“甲、乙至少有一人获奖”为事件,则为“甲、乙两人都未获奖”.
.
答:甲、乙至少有一人获奖的概率为.
12.(Ⅰ)(Ⅱ) 平均数74.9,众数75.14,中位数75;(Ⅲ)
【解析】
【分析】
(I)根据频率之和为列方程,结合求出的值.(II)利用各组中点值乘以频率然后相加,求得平均数.利用中位数是面积之和为的地方,列式求得中位数.以频率分布直方图最高一组的中点作为中位数.(III)先计算出从,中分别抽取人和人,再利用列举法和古典概型概率计算公式,计算出所求的概率.
【详解】
解:(I)依题意得,所以,
又,所以.
(Ⅱ)平均数为
中位数为
众数为
(Ⅲ)依题意,知分数在的市民抽取了2人,记为,分数在的市民抽取了6人,记为1,2,3,4,5,6,
所以从这8人中随机抽取2人所有的情况为:
,
共28种,
其中满足条件的为,共13种,设“至少有1人的分数在”的事件为,则
【点睛】
本小题主要考查求解频率分布直方图上的未知数,考查利用频率分布直方图估计平均数、中位数和众数的方法,考查利用古典概型求概率.属于中档题.
13.(1)561;(2)5984;(3)2100;(4)2555;(5)6090.
【解析】
(1)从余下的34种商品中,任选取2种,问题得以解决.
(2)从余下的34种可选商品中,任选取3种,问题得以解决.
(3)从20种真货中选取1件,从15种假货中选取2件,问题得以解决.
(4)分选取2种假货,选取3种假货两种情况,问题得以解决.
(5)选取3种的总数减去选取3种假货得情况,问题得以解决.
【详解】
解:(1)从余下的34种商品中,选取2种有 (种),
∴某一种假货必须在内的不同取法有561种.
(2)从余下的34种可选商品中,选取3种,有(种).
∴某一种假货不能在内的不同取法有5 984种.
(3)从20种真货中选取1件,从15种假货中选取2件有(种).
∴恰有2种假货在内的不同的取法有2 100种.
(4)选取2种假货有种,选取3种假货种,共有选取方式 (种).
∴至少有2种假货在内的不同的取法有2 555种.
(5)选取3种的总数为,选取3种假货有种,因此共有选取方式 (种).
∴至多有2种假货在内的不同的取法有6 090种.
【点睛】
本题主要考察了排列、组合及简单计数问题,考查学生分析解决问题的能力,属于中档题.
14.(1);(2)分布列答案见解析,数学期望:.
【解析】
【分析】
(1)若妮妮第一次就选到自己妈妈的概率为,若妮妮第一次没有选到自己妈妈,第二次选到自己妈妈的概率为,然后可得答案.
(2)由题意知的所有可能值为 ,分别求出其概率,列出分布列,由公式求出期望.
【详解】
(1)记“妮妮选到自己妈妈”为事件,则;
(2)由题意知的所有可能值为 ,
则, ,
, ,
∴随机变量的分布列:
则.
15.(1)0.10;(2)
【解析】
【分析】
(1)由图中小矩形的面积之和为1可得[140,170)的频率,再由频率之比即得;(2)先确定[140,150),[150,160),[160,170]三个区间的频率,再分层抽样,最后根据古典概型求出概率。
【详解】
(1)∵图中小矩形的面积之和为1,
∴[140,170)的频率为:1﹣(0.04+0.12+0.19+0.30)=0.35,
∵[140,150),[150,160),[160,170)的频率之比为4:2:1,
∴[150,160)的频率为0.10,
(2)∵区间[140,150)的频率为0.20,
∴[130,140),[140,150),[150,160)内的频率依次为0.30,0.20,0.10,
用分层抽样的方法在区间[130,160)内抽取一个容量为6的样本,
则在区间[130,140)内应抽取63,设为A1,A2,A3,
在区间[140,150)内应抽取62,记为B1,B2,
在区间[150,160)内应抽取61,记为C,
设“从样本中任意抽取2位同学,这2位同学都在区间[130,150)内”这事件M,
则所有的基本事件有15个,分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),
(A2,C),(A3,B1),(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),
事件M包含的基本事件有10种,分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),
∴这2位同学跳绳次数都在区间[130,150)内的概率P(M).
【点睛】
本题考查根据频率分布直方图求区间频率,以及分层抽样和古典概型,是常考题型。
16.(1);(2).
【解析】
【分析】
(1)根据频数图,利用分层抽样得电动自行车应抽取4辆,电动汽车应抽取5辆,再利用古典概型和对立事件求得:至少有一辆为电动汽车的概率为;
(2)由频数图,计算样本中100辆电动车共补助元,算出每辆电动车平均需补助的钱乘以可得估计出市政府执行此方案的预算.
【详解】
(1)根据分层抽样的原理,电动自行车应抽取(辆),
电动汽车应抽取(辆).
从9辆电动车中抽取2辆,设电动汽车和电动自行车分别为,,,,,,,,,
可得抽法总数为36种,
其中2辆均为电动自行车的有,,,,,,共6种.
“设从这9辆中随机抽取2辆,至少有一辆为电动汽车”为事件,
则.
(2)由条件可知,这100辆电动车中电动自行车60辆,电动汽车40辆,其中电池需要更换的电动自行车8辆,电动汽车1辆.根据补助方案可知,这100辆电动车共补助
(元).
由样本估计总体,市政府执行此方案的预算大约需要
(元).即为所求.
【点睛】
本题考查从图中抽取数据信息、古典概型计算概率、样本估计总体思想,考查基本数据处理能力.
17.(1)直方图见解析;(2)40;(3).
【解析】
(1)先求出在,内的频率,从而在,内的,由此能把频率分布直方图补充完整.
(2)这100天中空气质量等级为优的天数为,空气质量等级为良的天数为,
(3)选定的6天中有2天空气质量等级为优,有4天为良分别记为,和,,,,记事件“从这6天中任取两天,这两天的空气质量等级相同”为,利用列举法能坟出这两天的空气质量等级相同的概率.
【详解】
解:(1)因为AQI在内的频率为
所以AQI在内的
故频率分布直方图补充完整如图所示.
(2)这100天中空气质量等级为优的天数为
空气质量等级为良的天数为
(3)由(2)可知,选定的6天中有2天空气质量等级为优,有4天为良
分别记为和
记事件“从这6天中任取两天,这两天的空气质量等级相同”为M,
则事件M包含的基本事件有
共有7个基本事件
而从6天中任取两天包含的基本事件有
共有15个基本事件,
∴从这6天中任取两天,这两天的空气质量等级相同的概率
【点睛】
本题考查频率分布直方图的画法、频数、概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.
18.(1),,;(2)
【解析】
【分析】
(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,则再利用独立事件的概率计算公式,解方程组即可得到答案.
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,利用对立事件,即计算即可.
【详解】
(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,
由题设条件有即
解得,,.
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别是,,;
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,则
.
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为.
【点晴】
本题主要考查独立事件的概率计算问题,涉及到对立事件的概率计算,考查学生的数学运算能力,是一道容易题.
19.(1);(2);(3)
【解析】
【分析】
(1)直接利用排除法计算得到答案.
(2)根据乘法原理计算得到答案.
(3)将情况分为的组和的组,计算得到答案.
【详解】
(1)利用排除法:种.
(2)根据乘法原理得到:共有种涂法.
(3)若分成的组,则共有种分法;
若分成的组,则共有种分法,
故共有种放法.
【点睛】
本题考查了排列组合的应用,意在考查学生的计算能力和应用能力.
20.(1)属于;(2).
【解析】
(1)由频率分布直方图求出,从而得到具体的,即可判断.
(2)结合分层抽样的知识点首先求出前三组各抽多少人,然后结合排列组合的思想求出从6人中抽取2人的组合数以及恰有一人月薪不超过5000 元的组合数,最后由古典概型概率公式即可求出.
【详解】
(1)解: 由频率分布直方图知
则.在的左侧,
所以张铭属于“就业不理想”的学生.
(2)解:前三组频率之比为
所以抽取的6人中,第一组有1人,第二组有2人,第三组有3人.
从6人中再抽2人的组合数为种. 其中,恰有一人月薪不超过5000 元的组合数为
种.设”恰有1人月薪不超过5000 元”.则
所以获赠智能手机的2人中恰有1人月薪不超过5000 元的概率为.
【点睛】
本题考查了由频率分布直方图估计样本平均数,考查了古典概型,考查了分层抽样,考查了排列组合.本题的难点在于计算.易错点是记错求平均数公式,误用每个长方形的高与其横坐标中点相乘.
21.(1);(2)选方案好.
【解析】
(1)根据分层抽样找出金桔个数,然后找出所有事件,以及满足题目要求的事件,套用古典概型的概率公式,即可得到本题答案.
(2)根据两个不同的方案,计算出收益,判断最优方案.
【详解】
解:(1)由题,得金桔质量在和的比例为,
所以从质量落在,的金桔中分别取2个和3个,
记金桔中取的2个设为,金桔中取的3个设为,
有,共10个事件,
满足题目要求的有,,共9个事件,
所以2个金桔质量至少有一个不小于40克的概率为;
(2)方案好,理由如下:
由频率直方图可知:金桔质量在各个区间的频率依次为0.1,0.2,0.3,0.25,0.15.
各个区间的金桔个数为:10000,20000,30000,25000,15000,
若按方案销售:;
若按方案销售:
低于40克的金桔有个,不低于40克的金桔有70000个,
总收益有,
故选方案好.
【点睛】
本题主要考查频率直方图的应用,分层抽样以及古典概型的求法,考查学生分析问题和解决问题的能力,以及运算求解能力.
22.(1);(2)答案见详解.
【解析】
【分析】
(1)甲队最后赢得整场比赛的情况为第四局赢或第四局输第五局赢,算出答案即可.
(2)的取值只能为2,4或6,对应比分为,,,分别分析对应的情况,求出对应的概率即可.
【详解】
(1)甲队最后赢得整场比赛的情况为第四局赢或第四局输第五局赢,
所以甲队最后赢得整场比赛的概率为.
(2)根据比赛规则,的取值只能为2,4或6,对应比分为,,.
两队打了2个球后甲赢得整场比赛,即打第一个球甲发球甲得分,
打第二个球甲发球甲得分,此时概率为;
两队打了4个球后甲赢得整场比赛,即打第一个球甲发球甲得分,打第二个球甲发球甲失分,
打第三个球乙球甲发球甲得分,打第四个球甲发球甲得分,此时概率为.
两队打了6个球后甲赢得整场比赛,6个球的胜负情况如图(胜者用√表示),
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
1 2 3 4 5 6
甲 √ √ √ √
乙 √ √
答案第1页,共2页
答案第1页,共2页
