2021—2022学年人教版数学八年级下册17.2勾股定理的逆定理第二课时 课件(共32张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册17.2勾股定理的逆定理第二课时 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 08:28:45 | ||
图片预览










文档简介
(共32张PPT)
勾股定理的逆定理
第二课时
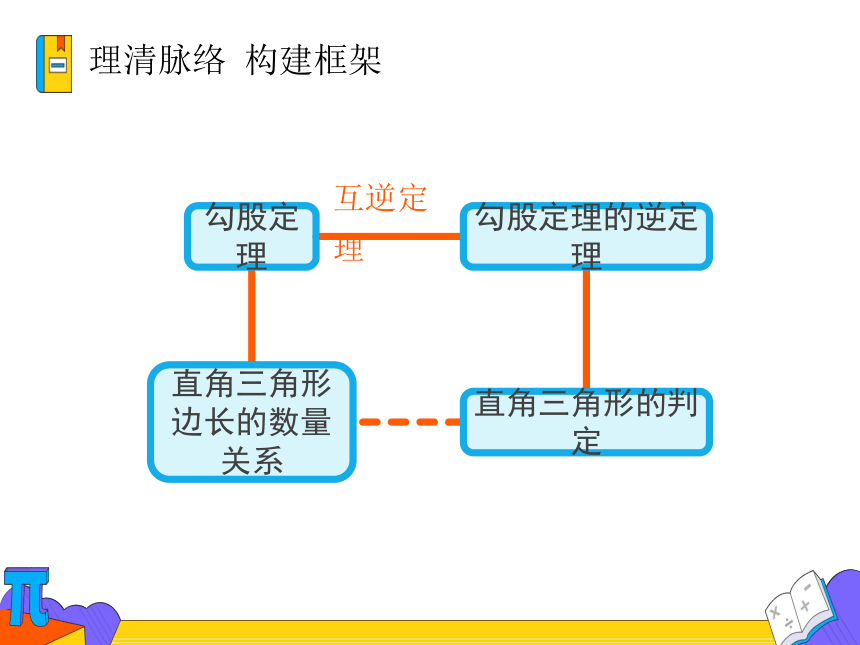
理清脉络 构建框架
勾股定理的逆定理
直角三角形边长的数量关系
直角三角形的判定
勾股定理
互逆定理
练习 在,,长为______.
基础训练 巩固知识
明确了直角三角形中哪条边是斜边.
所对的边为直角三角形的斜边.
第三边
2
练习 在,,长为____________.
基础训练 巩固知识
可能是斜边,也可能是第三边为斜边.
基础训练 巩固知识
练习 分别以下列四组数为一个三角形的边长:
基础训练 巩固知识
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
要判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方即可.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
以这三组数为边长的三角形都是直角三角形.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
以这组数为边长的三角形不是直角三角形.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
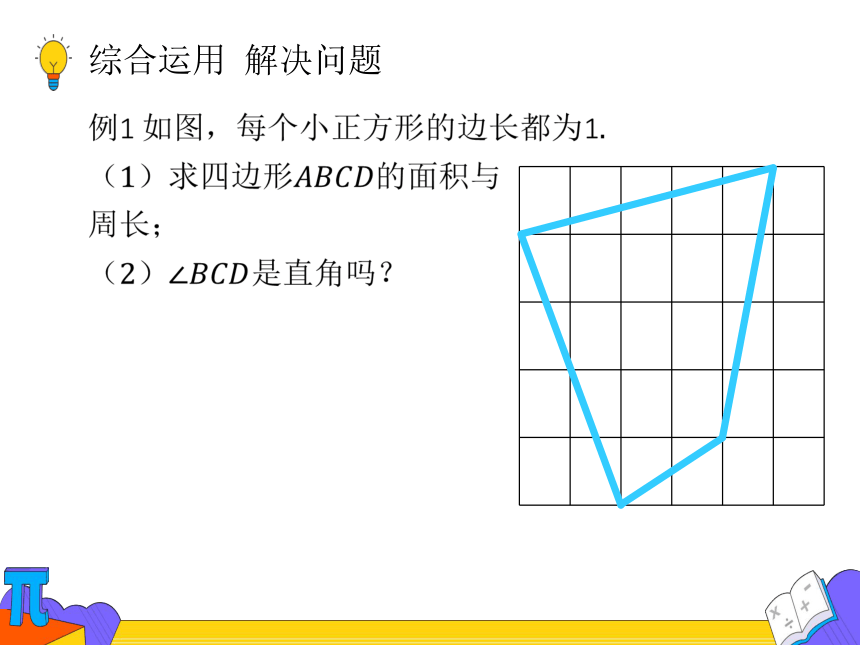
综合运用 解决问题
11
()求面积与
周长;
()是直角吗?
综合运用 解决问题
11
()求面积与周长;
()是直角吗?
解:()根据勾股定理可得:
所以
综合运用 解决问题
11
()求面积与
周长;
()是直角吗?
解:()
综合运用 解决问题
11
()求面积
与周长;
()是直角吗?
11
()求面积与
周长;
()是直角吗?
综合运用 解决问题
解:()
∴
例题讲解
例 已知,,的三边,且.
试判断形状,并说明理由.
提示:
答案:等腰三角形或直角三角形.
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
需要说明这三条线段在一个直角三角形中,并且DE是这个三角形的斜边.
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
再说明这个三角形是直角三角形.
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
巩固练习
通过认真的读题,把题目中所给的已知条件对应到相应的图形中.
在图形中解决问题.
练习 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,格子沿一固定方向航行,“远航”号每小时航行. “海天”号每小时航行.它们离开港口一个半小时候分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
练习 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,格子沿一固定方向航行,“远航”号每小时航行. “海天”号每小时航行.它们离开港口一个半小时候分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
巩固练习
解:根据题意,
练习 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,格子沿一固定方向航行,“远航”号每小时航行. “海天”号每小时航行.它们离开港口一个半小时候分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
巩固练习
解:根据题意,
“海天”号沿西北方向航行.
练习 如图,在四边形中,,. 点是的中点,点是上一点,且
:.
巩固练习
,只需证明是直角三角形.
利用勾股定理的逆定理,把三条边表示出来。
证明.
练习 如图,在四边形中,,. 点是的中点,点是上一点,且
:.
巩固练习
说明是直角三角形
课堂小结
勾股定理的逆定理
直角三角形边长的数量关系
直角三角形的判定
勾股定理
互逆定理
两个定理(勾股定理及其逆定理);
两种重要思想(出入相补思想、数形结合思想).
再 见
勾股定理的逆定理
第二课时
理清脉络 构建框架
勾股定理的逆定理
直角三角形边长的数量关系
直角三角形的判定
勾股定理
互逆定理
练习 在,,长为______.
基础训练 巩固知识
明确了直角三角形中哪条边是斜边.
所对的边为直角三角形的斜边.
第三边
2
练习 在,,长为____________.
基础训练 巩固知识
可能是斜边,也可能是第三边为斜边.
基础训练 巩固知识
练习 分别以下列四组数为一个三角形的边长:
基础训练 巩固知识
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
要判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方即可.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
以这三组数为边长的三角形都是直角三角形.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
以这组数为边长的三角形不是直角三角形.
练习 分别以下列四组数为一个三角形的边长:① ,,;② ,,; ③ ,,; ④ ,,. 其中能构成直角三角形的有____________.
基础训练 巩固知识
综合运用 解决问题
11
()求面积与
周长;
()是直角吗?
综合运用 解决问题
11
()求面积与周长;
()是直角吗?
解:()根据勾股定理可得:
所以
综合运用 解决问题
11
()求面积与
周长;
()是直角吗?
解:()
综合运用 解决问题
11
()求面积
与周长;
()是直角吗?
11
()求面积与
周长;
()是直角吗?
综合运用 解决问题
解:()
∴
例题讲解
例 已知,,的三边,且.
试判断形状,并说明理由.
提示:
答案:等腰三角形或直角三角形.
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
需要说明这三条线段在一个直角三角形中,并且DE是这个三角形的斜边.
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
再说明这个三角形是直角三角形.
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
例题讲解
例 如图都是等腰直角三角形,,D为AB边上一点.
求证:
巩固练习
通过认真的读题,把题目中所给的已知条件对应到相应的图形中.
在图形中解决问题.
练习 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,格子沿一固定方向航行,“远航”号每小时航行. “海天”号每小时航行.它们离开港口一个半小时候分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
练习 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,格子沿一固定方向航行,“远航”号每小时航行. “海天”号每小时航行.它们离开港口一个半小时候分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
巩固练习
解:根据题意,
练习 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,格子沿一固定方向航行,“远航”号每小时航行. “海天”号每小时航行.它们离开港口一个半小时候分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
巩固练习
解:根据题意,
“海天”号沿西北方向航行.
练习 如图,在四边形中,,. 点是的中点,点是上一点,且
:.
巩固练习
,只需证明是直角三角形.
利用勾股定理的逆定理,把三条边表示出来。
证明.
练习 如图,在四边形中,,. 点是的中点,点是上一点,且
:.
巩固练习
说明是直角三角形
课堂小结
勾股定理的逆定理
直角三角形边长的数量关系
直角三角形的判定
勾股定理
互逆定理
两个定理(勾股定理及其逆定理);
两种重要思想(出入相补思想、数形结合思想).
再 见
