人教版数学七年级下册 5.4 平移 课件(共38张)
文档属性
| 名称 | 人教版数学七年级下册 5.4 平移 课件(共38张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 09:45:41 | ||
图片预览








文档简介
(共38张PPT)
人教版 · 数学· 七年级(下)
第五章 相交线与平行线
5.4 平移
1.通过实例认识平移,理解平移的含义和性质.
2.会找出平移前后图形中对应点和对应线段.
3.能按要求作出简单平面图形平移后的图形,培养观察和动手操作的能力.
学习目标
仔细观察下列美丽的图案,回答问题:
1.这些图案有什么共同特点?
2.下面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的吗?
新知一 平移的有关概念
合作探究
1.这些图案有什么共同特点?
2.上面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的吗?
现在你能回答出刚才提出的问题了吗?
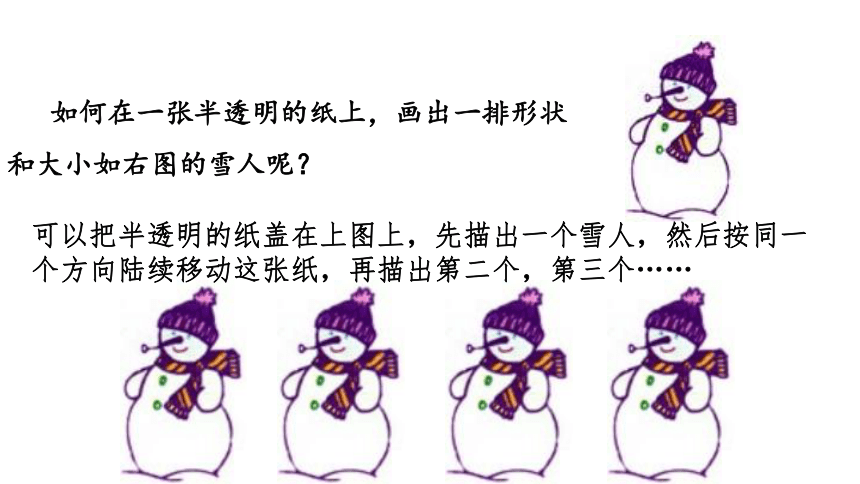
如何在一张半透明的纸上,画出一排形状和大小如右图的雪人呢?
可以把半透明的纸盖在上图上,先描出一个雪人,然后按同一个方向陆续移动这张纸,再描出第二个,第三个……
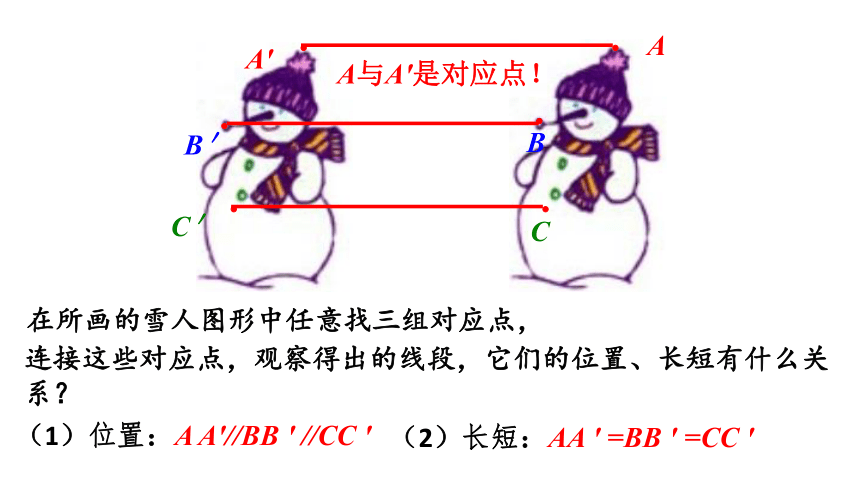
在所画的雪人图形中任意找三组对应点,
连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
(1)位置:A A′//BB ′ //CC ′
(2)长短:AA ′ =BB ′ =CC ′
A′
A
A与A′是对应点!
B'
B
C'
C
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.
特征:
(1)平移不改变图形的形状和大小.
(2)连接各组对应点的线段平行且相等.
【思考】1.图形平移的方向一定是水平的吗?
2.图形平移的位置由什么确定
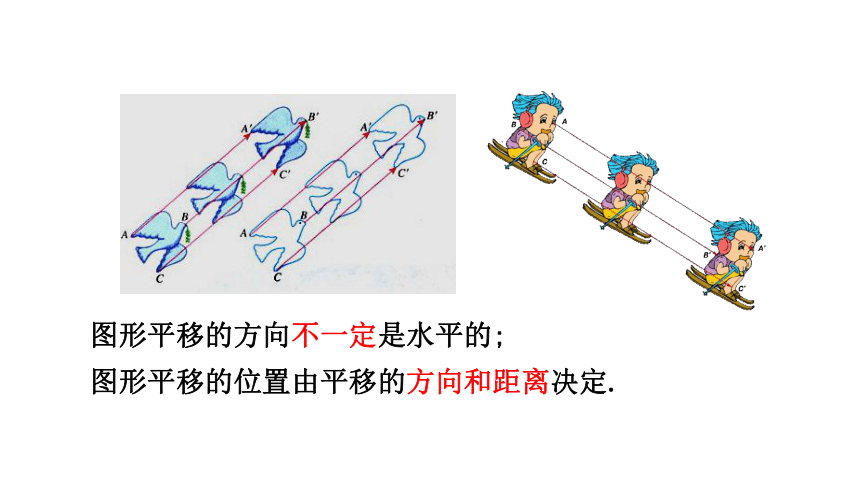
图形平移的方向不一定是水平的;
图形平移的位置由平移的方向和距离决定.
(1)平移只改变图形的位置,不改变图形的形状、大小、方向.
(2)平移的方向可以是任意的,只要是直线方向即可.
(3)图形的平移是整个图形都在移动,即图形中所有的点、线平移的方向、距离都相同.
(4)确定一个图形平移的方向和距离,只需确定其上一个点平移的方向和距离即可.
归纳小结
例1 下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段平直的铁轨上;(5)沸水中气泡的运动.
属于平移的是_______________.
典例精析1 平移现象的识别
平移
旋转
平移
旋转
平移
(1)(2)(4)
提示:判断生活中的现象是否是平移,要根据平移的定义,进行判断,图形平移前后的形状和大小没有变化,只是位置发生变化.
合作探究
下列实例属于平移的是( )
A.分针的运行 B.转动的摩天轮
C.直线行驶的火车 D.地球自转
C
在以下现象中:①水管里水的流动;②打针时针管的移动;③射出的子弹;④汽车在笔直平坦的公路上行驶. 其中是平移的是( )
A. ①② B. ①③ C. ②③ D. ②④
D
巩固新知
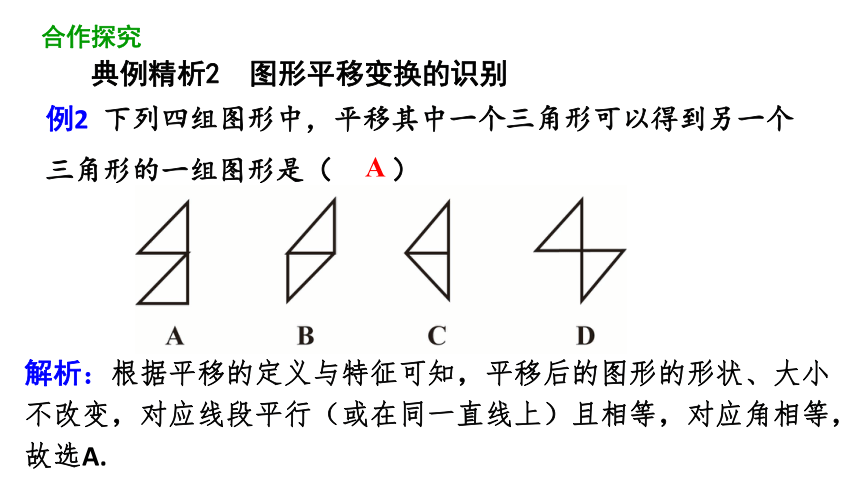
例2 下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )
解析:根据平移的定义与特征可知,平移后的图形的形状、大小不改变,对应线段平行(或在同一直线上)且相等,对应角相等,故选A.
典例精析2 图形平移变换的识别
A
合作探究
下列图形变换属于平移的有哪些?
√
√
×
×
×
×
巩固新知
动动手:用三角板、直尺画平行线.
P
Q
D
E
F
A
B
C
AB//DE.
AB=DE,
AC//DF .
AC=DF,
观察:线段AB与DE的位置关系
与数量关系.
观察:线段AC与DF的位置关系
与数量关系.
新知二 平移的性质
直尺PQ是倾斜放置,用三角板能否画出平行线?
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
合作探究
规律小结
1.平移后的图形与原来的图形的对应线段平行且相等;
2.在平移过程中,对应线段也可能在一条直线上,如BC与EF;
3.平移后图形的形状与大小都没有变化;
4.平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的
长度.
问题:三角形ABC沿着PQ的方向平移到 △A'B'C'的位置,除了对应线段平行且相等外,你还发现了什么现象?
B
A
C
P
Q
A
A'
B
B'
C
C'
AA'//____//____
AA'=____=____
BB'
CC'
CC'
BB'
M
M'
R
S
BC的中点M平移到什么地方去了?
几何符号语言:
①平移的两个图形形状和大小完全相同;
A
B
C
D
E
F
A
B
C
D
E
F
∵三角形ABC平移得到三角
形DEF,
∴AB∥DE,AC∥DF,
BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等.
图形平移的基本性质:
AA'
AA'
C
AA'
AA'
B'
C'
例1 如图,平移三角形ABC,使点A移动
到点A',画出平移后的三角形A'B'C'.
解:(1)连接 ,
(2)过点B作AA'的平行线, 在上截取BB'= ,
(3)过点 作 的平行线,在上截取
CC'= ,
(4)连接A'B',B'C',A'C',
所得的三角形就是平移后的
三角形.
典例精析1 平移作图
A
B
C
A'
平移作图是平移性质的应用.在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
归纳小结
B
D
F
如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,
请画出点A的对应点D、点C的对应点F的位置,连接△DEF.
A
C
E
巩固新知
1m
1m
21m
15m
A
C
D
B
图 1
例2 如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的
面积为
多少
1m
1m
21m
15m
A
C
D
B
图 1
提示:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
典例精析2 利用平移求面积
合作探究
1m
21m
15m
A
C
D
B
【思考】如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
提示:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
如图所示,图中小正方形的边长为a,则阴影部分的面积是________.
a2
巩固新知
1.(3分)下列情形中,不属于平移的有( )
A.钟表的指针转动
B.电梯上人的升降
C.火车在笔直的铁轨上行驶
D.农村辘轳上水桶的升降
2.(3分)下列四幅名车标志设计中能用平移得到的是( )
A
A
课堂练习
3.(4分)如图,三角形ABC经过平移后得到三角形DEF,下列结论:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
4.(4分)如图,三角形A′B′C′是由三角形ABC沿射线AC方向平移2 cm得到,若AC=3 cm,则A′C=_________.
1cm
5.(6分)如图,在Rt△ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,
将△ABC沿AB方向向右平移得到△DEF,若AE=8 cm,DB=2 cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
解:(1)3 cm (2)18 cm
6.(4分)(广州中考)在6×6的方格中,将图①中的图形N平移后,如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
D
7.(6分)如图所示,通过平移,把三角形ABC的顶点A移到点D,画出平移后的图形.
解:如图所示,三角形DEF即为所求
1.关键在于按要求作出对应点;
2.然后,顺次连接对应点即可.
1.平移前后图形的形状和大小完全相同;
2.对应线段平行(或在同一直线
上)且相等;
平移的概念
平移的性质
平移
作图
平移
3.各对应点所连线段平行(或在
同一直线上)且相等.
归纳新知
1.(新疆中考)如图,将△ABC沿BC方向平移1 cm得到△DEF,
若△ABC的周长为8 cm,则四边形ABFD的周长为( )
A.10 cm B.18 cm
C.20 cm D.22 cm
A
课后练习
2.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,
现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
D
3.(铜仁中考)如图,三角形ABC沿着BC方向平移得到三角形A′B′C′,P是直线AA′上任意一点,若三角形ABC,三角形PB′C′的面积分别为S1,S2,则下列关系正确的是( )
A.S1>S2 B.S1<S2
C.S1=S2 D.S1=2S2
C
4.如图,把∠AOB沿着直线MN平移一定距离得到∠CPD,若∠AOM=40°,∠DPN=40°,则∠AOB的度数为__________.
5.如图,将面积为9的△ABC沿BC方向平移2个单位得到△A1B1C1.若B1C=4,则△A1B1C1的底边B1C1上的高为____.
100°
3
6.如图所示,某中学校园内有一块长30米,宽24米的草地,
中间有两条2米宽的小路,把草地分成4块,求草地的面积.
解:S=(30-2)×(24-2)=616(平方米)
7.如图,将Rt△ABC沿CB方向平移BE的距离后得到Rt△DEF,
已知AG=2,BE=4,DE=6,求阴影部分的面积.
8.(1)已知图①将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图④,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求剩下部分的面积.
解:(1)图略 (2)面积均为ab-b (3)390 m2
再见
人教版 · 数学· 七年级(下)
第五章 相交线与平行线
5.4 平移
1.通过实例认识平移,理解平移的含义和性质.
2.会找出平移前后图形中对应点和对应线段.
3.能按要求作出简单平面图形平移后的图形,培养观察和动手操作的能力.
学习目标
仔细观察下列美丽的图案,回答问题:
1.这些图案有什么共同特点?
2.下面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的吗?
新知一 平移的有关概念
合作探究
1.这些图案有什么共同特点?
2.上面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的吗?
现在你能回答出刚才提出的问题了吗?
如何在一张半透明的纸上,画出一排形状和大小如右图的雪人呢?
可以把半透明的纸盖在上图上,先描出一个雪人,然后按同一个方向陆续移动这张纸,再描出第二个,第三个……
在所画的雪人图形中任意找三组对应点,
连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
(1)位置:A A′//BB ′ //CC ′
(2)长短:AA ′ =BB ′ =CC ′
A′
A
A与A′是对应点!
B'
B
C'
C
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.
特征:
(1)平移不改变图形的形状和大小.
(2)连接各组对应点的线段平行且相等.
【思考】1.图形平移的方向一定是水平的吗?
2.图形平移的位置由什么确定
图形平移的方向不一定是水平的;
图形平移的位置由平移的方向和距离决定.
(1)平移只改变图形的位置,不改变图形的形状、大小、方向.
(2)平移的方向可以是任意的,只要是直线方向即可.
(3)图形的平移是整个图形都在移动,即图形中所有的点、线平移的方向、距离都相同.
(4)确定一个图形平移的方向和距离,只需确定其上一个点平移的方向和距离即可.
归纳小结
例1 下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段平直的铁轨上;(5)沸水中气泡的运动.
属于平移的是_______________.
典例精析1 平移现象的识别
平移
旋转
平移
旋转
平移
(1)(2)(4)
提示:判断生活中的现象是否是平移,要根据平移的定义,进行判断,图形平移前后的形状和大小没有变化,只是位置发生变化.
合作探究
下列实例属于平移的是( )
A.分针的运行 B.转动的摩天轮
C.直线行驶的火车 D.地球自转
C
在以下现象中:①水管里水的流动;②打针时针管的移动;③射出的子弹;④汽车在笔直平坦的公路上行驶. 其中是平移的是( )
A. ①② B. ①③ C. ②③ D. ②④
D
巩固新知
例2 下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )
解析:根据平移的定义与特征可知,平移后的图形的形状、大小不改变,对应线段平行(或在同一直线上)且相等,对应角相等,故选A.
典例精析2 图形平移变换的识别
A
合作探究
下列图形变换属于平移的有哪些?
√
√
×
×
×
×
巩固新知
动动手:用三角板、直尺画平行线.
P
Q
D
E
F
A
B
C
AB//DE.
AB=DE,
AC//DF .
AC=DF,
观察:线段AB与DE的位置关系
与数量关系.
观察:线段AC与DF的位置关系
与数量关系.
新知二 平移的性质
直尺PQ是倾斜放置,用三角板能否画出平行线?
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
合作探究
规律小结
1.平移后的图形与原来的图形的对应线段平行且相等;
2.在平移过程中,对应线段也可能在一条直线上,如BC与EF;
3.平移后图形的形状与大小都没有变化;
4.平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的
长度.
问题:三角形ABC沿着PQ的方向平移到 △A'B'C'的位置,除了对应线段平行且相等外,你还发现了什么现象?
B
A
C
P
Q
A
A'
B
B'
C
C'
AA'//____//____
AA'=____=____
BB'
CC'
CC'
BB'
M
M'
R
S
BC的中点M平移到什么地方去了?
几何符号语言:
①平移的两个图形形状和大小完全相同;
A
B
C
D
E
F
A
B
C
D
E
F
∵三角形ABC平移得到三角
形DEF,
∴AB∥DE,AC∥DF,
BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等.
图形平移的基本性质:
AA'
AA'
C
AA'
AA'
B'
C'
例1 如图,平移三角形ABC,使点A移动
到点A',画出平移后的三角形A'B'C'.
解:(1)连接 ,
(2)过点B作AA'的平行线, 在上截取BB'= ,
(3)过点 作 的平行线,在上截取
CC'= ,
(4)连接A'B',B'C',A'C',
所得的三角形就是平移后的
三角形.
典例精析1 平移作图
A
B
C
A'
平移作图是平移性质的应用.在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
归纳小结
B
D
F
如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,
请画出点A的对应点D、点C的对应点F的位置,连接△DEF.
A
C
E
巩固新知
1m
1m
21m
15m
A
C
D
B
图 1
例2 如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的
面积为
多少
1m
1m
21m
15m
A
C
D
B
图 1
提示:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
典例精析2 利用平移求面积
合作探究
1m
21m
15m
A
C
D
B
【思考】如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
提示:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
如图所示,图中小正方形的边长为a,则阴影部分的面积是________.
a2
巩固新知
1.(3分)下列情形中,不属于平移的有( )
A.钟表的指针转动
B.电梯上人的升降
C.火车在笔直的铁轨上行驶
D.农村辘轳上水桶的升降
2.(3分)下列四幅名车标志设计中能用平移得到的是( )
A
A
课堂练习
3.(4分)如图,三角形ABC经过平移后得到三角形DEF,下列结论:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
4.(4分)如图,三角形A′B′C′是由三角形ABC沿射线AC方向平移2 cm得到,若AC=3 cm,则A′C=_________.
1cm
5.(6分)如图,在Rt△ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,
将△ABC沿AB方向向右平移得到△DEF,若AE=8 cm,DB=2 cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
解:(1)3 cm (2)18 cm
6.(4分)(广州中考)在6×6的方格中,将图①中的图形N平移后,如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
D
7.(6分)如图所示,通过平移,把三角形ABC的顶点A移到点D,画出平移后的图形.
解:如图所示,三角形DEF即为所求
1.关键在于按要求作出对应点;
2.然后,顺次连接对应点即可.
1.平移前后图形的形状和大小完全相同;
2.对应线段平行(或在同一直线
上)且相等;
平移的概念
平移的性质
平移
作图
平移
3.各对应点所连线段平行(或在
同一直线上)且相等.
归纳新知
1.(新疆中考)如图,将△ABC沿BC方向平移1 cm得到△DEF,
若△ABC的周长为8 cm,则四边形ABFD的周长为( )
A.10 cm B.18 cm
C.20 cm D.22 cm
A
课后练习
2.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,
现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
D
3.(铜仁中考)如图,三角形ABC沿着BC方向平移得到三角形A′B′C′,P是直线AA′上任意一点,若三角形ABC,三角形PB′C′的面积分别为S1,S2,则下列关系正确的是( )
A.S1>S2 B.S1<S2
C.S1=S2 D.S1=2S2
C
4.如图,把∠AOB沿着直线MN平移一定距离得到∠CPD,若∠AOM=40°,∠DPN=40°,则∠AOB的度数为__________.
5.如图,将面积为9的△ABC沿BC方向平移2个单位得到△A1B1C1.若B1C=4,则△A1B1C1的底边B1C1上的高为____.
100°
3
6.如图所示,某中学校园内有一块长30米,宽24米的草地,
中间有两条2米宽的小路,把草地分成4块,求草地的面积.
解:S=(30-2)×(24-2)=616(平方米)
7.如图,将Rt△ABC沿CB方向平移BE的距离后得到Rt△DEF,
已知AG=2,BE=4,DE=6,求阴影部分的面积.
8.(1)已知图①将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图④,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求剩下部分的面积.
解:(1)图略 (2)面积均为ab-b (3)390 m2
再见
