华东师大版七年级下册数学 10.3.1 图形的旋转 教案(表格形式)
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.1 图形的旋转 教案(表格形式) |
|
|
| 格式 | docx | ||
| 文件大小 | 84.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览

文档简介
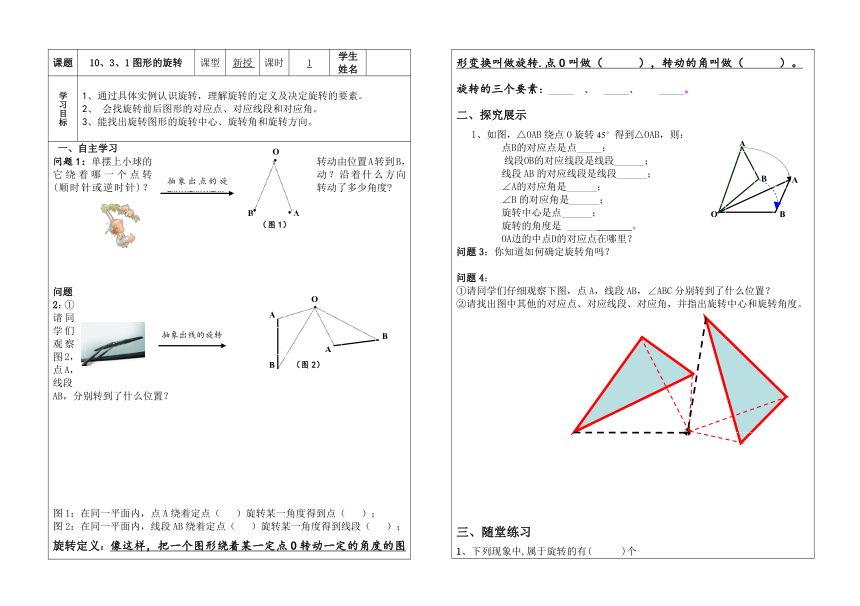
课题 10、3、1图形的旋转 课型 新授 课时 1 学生姓名
学习目标 通过具体实例认识旋转,理解旋转的定义及决定旋转的要素。 会找旋转前后图形的对应点、对应线段和对应角。 能找出旋转图形的旋转中心、旋转角和旋转方向。
一、自主学习 问题1:单摆上小球的转动由位置A转到B,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度 ··○○○ 问题2:①请同学们观察图2,点A,线段AB,分别转到了什么位置? (
抽象出线的旋转
·
O
A
B
A
B
(图2)
) (
抽象出点的旋ZHUANZHUANZHUAN转
B
A
(图1)
O
) 图1:在同一平面内,点A绕着定点( )旋转某一角度得到点( ); 图2:在同一平面内,线段AB绕着定点( )旋转某一角度得到线段( ); 旋转定义:像这样,把一个图形绕着某一定点O转动一定的角度的图形变换叫做旋转.点O叫做( ),转动的角叫做( )。 旋转的三个要素:_____ 、 _____、 _____。 二、探究展示 (
A
A
B
O
B
)1、如图,△OAB绕点O旋转45°得到△OAB,则: 点B的对应点是点_____; 线段OB的对应线段是线段______; 线段AB的对应线段是线段______; ∠A的对应角是______; ∠B的对应角是______; 旋转中心是点______; 旋转的角度是 ______ 。 OA边的中点D的对应点在哪里? 问题3:你知道如何确定旋转角吗? 问题4: ①请同学们仔细观察下图,点A,线段AB,∠ABC分别转到了什么位置? ②请找出图中其他的对应点、对应线段、对应角,并指出旋转中心和旋转角度。 随堂练习 1、下列现象中,属于旋转的有( )个 ①地下水位逐年下降; ②传送带的移动; ③方向盘的转动; ④水龙头开关的转动; ⑤钟摆的运动; ⑥荡秋千运动. A.2 B.3 C.4 D.5 例1、如图:△ABC是等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置 。 旋转中心是哪一点? 旋转了多少度? (3)如果M是AB上中点,那么经过上述的旋转后,点M到了什么位置? 例2、如图11.2.7(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢? 2.每组图形中的一个是怎样旋转变换成另一个的? (
A
C
B
D
E
) (
A
C
E
B
D
) 两个直角三角形 两个等腰直角三角形 四、能力提升 如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案 (
B
A
C
D
E
F
) 五、自我小结
学习目标 通过具体实例认识旋转,理解旋转的定义及决定旋转的要素。 会找旋转前后图形的对应点、对应线段和对应角。 能找出旋转图形的旋转中心、旋转角和旋转方向。
一、自主学习 问题1:单摆上小球的转动由位置A转到B,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度 ··○○○ 问题2:①请同学们观察图2,点A,线段AB,分别转到了什么位置? (
抽象出线的旋转
·
O
A
B
A
B
(图2)
) (
抽象出点的旋ZHUANZHUANZHUAN转
B
A
(图1)
O
) 图1:在同一平面内,点A绕着定点( )旋转某一角度得到点( ); 图2:在同一平面内,线段AB绕着定点( )旋转某一角度得到线段( ); 旋转定义:像这样,把一个图形绕着某一定点O转动一定的角度的图形变换叫做旋转.点O叫做( ),转动的角叫做( )。 旋转的三个要素:_____ 、 _____、 _____。 二、探究展示 (
A
A
B
O
B
)1、如图,△OAB绕点O旋转45°得到△OAB,则: 点B的对应点是点_____; 线段OB的对应线段是线段______; 线段AB的对应线段是线段______; ∠A的对应角是______; ∠B的对应角是______; 旋转中心是点______; 旋转的角度是 ______ 。 OA边的中点D的对应点在哪里? 问题3:你知道如何确定旋转角吗? 问题4: ①请同学们仔细观察下图,点A,线段AB,∠ABC分别转到了什么位置? ②请找出图中其他的对应点、对应线段、对应角,并指出旋转中心和旋转角度。 随堂练习 1、下列现象中,属于旋转的有( )个 ①地下水位逐年下降; ②传送带的移动; ③方向盘的转动; ④水龙头开关的转动; ⑤钟摆的运动; ⑥荡秋千运动. A.2 B.3 C.4 D.5 例1、如图:△ABC是等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置 。 旋转中心是哪一点? 旋转了多少度? (3)如果M是AB上中点,那么经过上述的旋转后,点M到了什么位置? 例2、如图11.2.7(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢? 2.每组图形中的一个是怎样旋转变换成另一个的? (
A
C
B
D
E
) (
A
C
E
B
D
) 两个直角三角形 两个等腰直角三角形 四、能力提升 如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案 (
B
A
C
D
E
F
) 五、自我小结
