华东师大版七年级下册数学 10.1.2 轴对称的再认识 教案
文档属性
| 名称 | 华东师大版七年级下册数学 10.1.2 轴对称的再认识 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 10:28:29 | ||
图片预览


文档简介
主备教师 使用教师 科目 数学
班级 8.5 课型 复习课 时间
课题 轴对称的应用
教 学 目 标 知识与能力目标 梳理本章重点内容,掌握简单的轴对称图形的性质并灵活应用;综合运用轴对称的有关性质,解决实际问题。
过程与方法目标 让学生在丰富的现实情境中,经历归纳、观察、分析、交流等数学活动过程,进一步发展空间观念,丰富学生对轴对称的直观体验和理解,发展学生有条理的思考和语言表达能力.
情感态度与价值观 在数学活动中发展学生合作交流的能力和数学表达能力,感受数学与现实生活的密切联系,增强学生的数学应用意识. 让学生进一步了解轴对称在现实生活中的广泛应用和丰富的文化价值,增进学生学习数学的兴趣.
教学重点分析 理解轴对称图形的有关性质,并体验轴对称在现实生活中的广泛应用.
教学难点分析 轴对称的有关性质在现实生活中的应用。
课前准备 多媒体课件
学情分析 立足学生已有的生活经验和初步的数学活动经历,从生活的角度研究轴对称,是本章基本的出发点。因此,在本章结束时,针对应用本章知识点典型题型进行总结归纳,是提高学生迁移应用能力的保障。为了更好地引导学生运用“数学”的眼光观察现实世界,体会数学的广泛应用和文化价值,丰富学生的数学活动经验和体验,有意识地培养他们积极的情感、态度,促进观察、分析、归纳、概括等一般能力和审美意识的发展。
教学过程
导入自学 一.激疑引趣: 相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题: 从图中的A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路线全程最短? 精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马问题”. 你知道海伦是如何帮助将军解决问题的吗? 个性 调整
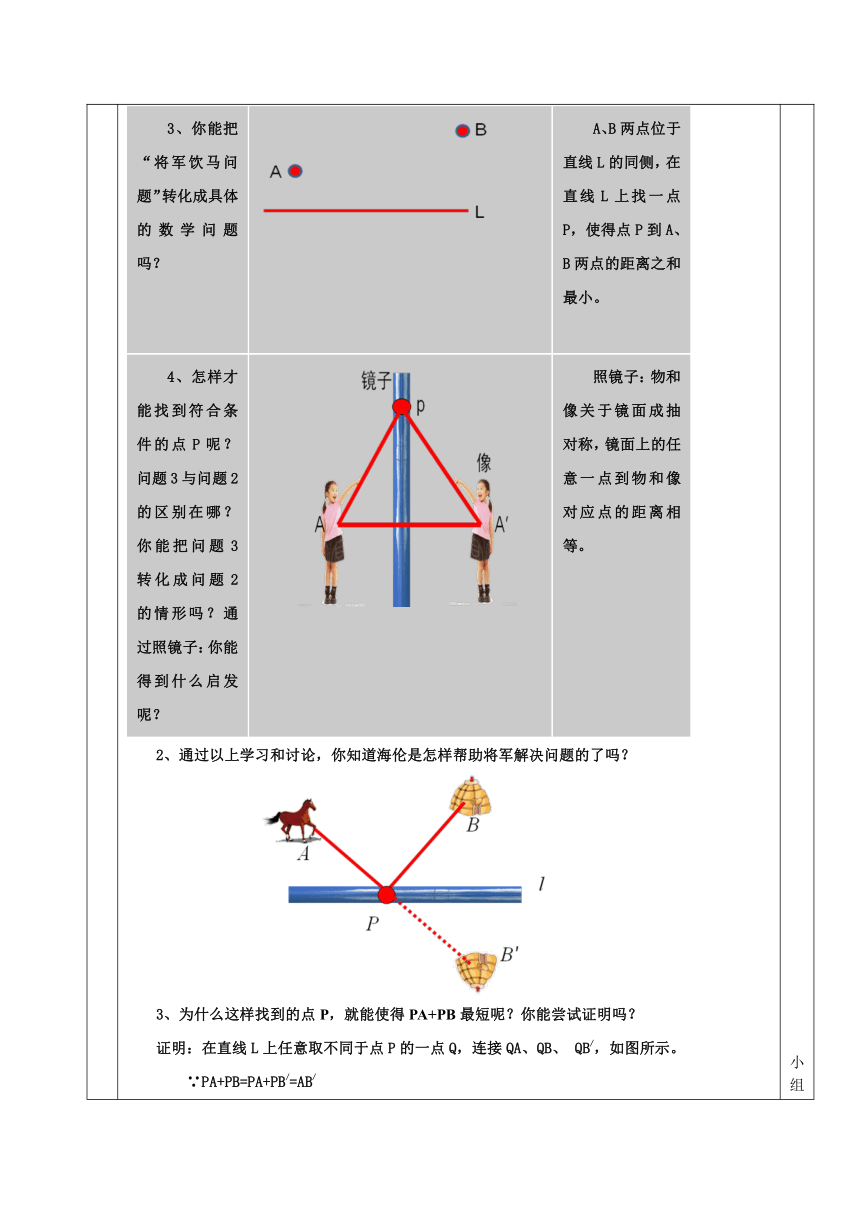
探 究 展 示 二、 活动一:任务驱动 启迪智慧------利用轴对称的性质尝试解决问题 1、梳理所学,完成任务清单。 问题 图形 语言描述 1、截至目前,你学到那些最短问题? 两点之间,线段最短直线外一点与直线上所有点的连线中,垂线段最短。 2、如图,A,B两点位于直线L的两侧,你能在直线L上找一点P,使得点p到A、B两点距离之和最短吗? 将直线异侧的两点A、B直接连接,交直线L于点P,此时PA+PB最短。 3、你能把“将军饮马问题”转化成具体的数学问题吗? A、B两点位于直线L的同侧,在直线L上找一点P,使得点P到A、B两点的距离之和最小。 4、怎样才能找到符合条件的点P呢?问题3与问题2的区别在哪?你能把问题3转化成问题2的情形吗?通过照镜子:你能得到什么启发呢?照镜子:物和像关于镜面成抽对称,镜面上的任意一点到物和像对应点的距离相等。
2、通过以上学习和讨论,你知道海伦是怎样帮助将军解决问题的了吗? 3、为什么这样找到的点P,就能使得PA+PB最短呢?你能尝试证明吗? 证明:在直线L上任意取不同于点P的一点Q,连接QA、QB、 QB/,如图所示。 ∵PA+PB=PA+PB/=AB/ QA+QB=QA+QB/ 又∵AB/<QA+QB/(两点之间线段最短或三角形中两边之和大于第三边) ∴PA+PB< QA+QB 即此时点P使得PA+PB的值最小 三、小试牛刀 1、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,已知居民区A、B分别距离街道1km、2km,两居民区水平距离4km,请问奶站修建在什么地方才能使得A,B到它的距离之和最短?最短距离是多少? 四、再攀高峰------迁移应用 如图,A为马厩,B为帐篷,牧马人要从马厩牵出马,先到草地某一处牧马,再到河边饮水,然后回到帐篷,请帮他确定这一天的最短路线 五、小试牛刀 民中造桥选址问题:如图,民中学生宿舍A和教学楼B在小米溪河的两岸,现要在河上造一座桥MN.桥造在何处才能使同学们上学路程最短?(假定河的两岸是平行的直线,桥要与河垂直) 六、课堂小结 归纳提升 同学们,通过本堂课的学习,你学到了哪些知识?有哪些收获? 1、平面上,在直线上找一点使得到线外两定点的距离之和最小。 2、本节课所用到的数学思想:转化与化归 七、课后作业 1、如图,菱形ABCD中,AB=2, ∠BAD=600,E是AB的中点,点P是对角线AC上的一个动点,请找出使得PE+PB的值最小时点P的位置(找出位置即可) ☆ 2、利用轴对称的性质,类比本节课所学尝试在直线l上找一点P,让PB与PA的差最大,并给出证明! 独立 思考 小组 合作 独立完成 小组合作交流 梳理归纳 提升学生概括能力 分层作业 因材施教
班级 8.5 课型 复习课 时间
课题 轴对称的应用
教 学 目 标 知识与能力目标 梳理本章重点内容,掌握简单的轴对称图形的性质并灵活应用;综合运用轴对称的有关性质,解决实际问题。
过程与方法目标 让学生在丰富的现实情境中,经历归纳、观察、分析、交流等数学活动过程,进一步发展空间观念,丰富学生对轴对称的直观体验和理解,发展学生有条理的思考和语言表达能力.
情感态度与价值观 在数学活动中发展学生合作交流的能力和数学表达能力,感受数学与现实生活的密切联系,增强学生的数学应用意识. 让学生进一步了解轴对称在现实生活中的广泛应用和丰富的文化价值,增进学生学习数学的兴趣.
教学重点分析 理解轴对称图形的有关性质,并体验轴对称在现实生活中的广泛应用.
教学难点分析 轴对称的有关性质在现实生活中的应用。
课前准备 多媒体课件
学情分析 立足学生已有的生活经验和初步的数学活动经历,从生活的角度研究轴对称,是本章基本的出发点。因此,在本章结束时,针对应用本章知识点典型题型进行总结归纳,是提高学生迁移应用能力的保障。为了更好地引导学生运用“数学”的眼光观察现实世界,体会数学的广泛应用和文化价值,丰富学生的数学活动经验和体验,有意识地培养他们积极的情感、态度,促进观察、分析、归纳、概括等一般能力和审美意识的发展。
教学过程
导入自学 一.激疑引趣: 相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题: 从图中的A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路线全程最短? 精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马问题”. 你知道海伦是如何帮助将军解决问题的吗? 个性 调整
探 究 展 示 二、 活动一:任务驱动 启迪智慧------利用轴对称的性质尝试解决问题 1、梳理所学,完成任务清单。 问题 图形 语言描述 1、截至目前,你学到那些最短问题? 两点之间,线段最短直线外一点与直线上所有点的连线中,垂线段最短。 2、如图,A,B两点位于直线L的两侧,你能在直线L上找一点P,使得点p到A、B两点距离之和最短吗? 将直线异侧的两点A、B直接连接,交直线L于点P,此时PA+PB最短。 3、你能把“将军饮马问题”转化成具体的数学问题吗? A、B两点位于直线L的同侧,在直线L上找一点P,使得点P到A、B两点的距离之和最小。 4、怎样才能找到符合条件的点P呢?问题3与问题2的区别在哪?你能把问题3转化成问题2的情形吗?通过照镜子:你能得到什么启发呢?照镜子:物和像关于镜面成抽对称,镜面上的任意一点到物和像对应点的距离相等。
2、通过以上学习和讨论,你知道海伦是怎样帮助将军解决问题的了吗? 3、为什么这样找到的点P,就能使得PA+PB最短呢?你能尝试证明吗? 证明:在直线L上任意取不同于点P的一点Q,连接QA、QB、 QB/,如图所示。 ∵PA+PB=PA+PB/=AB/ QA+QB=QA+QB/ 又∵AB/<QA+QB/(两点之间线段最短或三角形中两边之和大于第三边) ∴PA+PB< QA+QB 即此时点P使得PA+PB的值最小 三、小试牛刀 1、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,已知居民区A、B分别距离街道1km、2km,两居民区水平距离4km,请问奶站修建在什么地方才能使得A,B到它的距离之和最短?最短距离是多少? 四、再攀高峰------迁移应用 如图,A为马厩,B为帐篷,牧马人要从马厩牵出马,先到草地某一处牧马,再到河边饮水,然后回到帐篷,请帮他确定这一天的最短路线 五、小试牛刀 民中造桥选址问题:如图,民中学生宿舍A和教学楼B在小米溪河的两岸,现要在河上造一座桥MN.桥造在何处才能使同学们上学路程最短?(假定河的两岸是平行的直线,桥要与河垂直) 六、课堂小结 归纳提升 同学们,通过本堂课的学习,你学到了哪些知识?有哪些收获? 1、平面上,在直线上找一点使得到线外两定点的距离之和最小。 2、本节课所用到的数学思想:转化与化归 七、课后作业 1、如图,菱形ABCD中,AB=2, ∠BAD=600,E是AB的中点,点P是对角线AC上的一个动点,请找出使得PE+PB的值最小时点P的位置(找出位置即可) ☆ 2、利用轴对称的性质,类比本节课所学尝试在直线l上找一点P,让PB与PA的差最大,并给出证明! 独立 思考 小组 合作 独立完成 小组合作交流 梳理归纳 提升学生概括能力 分层作业 因材施教
