华东师大版七年级下册数学 10.5 图形的全等 课件(共15张)
文档属性
| 名称 | 华东师大版七年级下册数学 10.5 图形的全等 课件(共15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 934.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 10:48:24 | ||
图片预览




文档简介
(共15张PPT)
图形的全等
我们已经认识了图形的翻折、平移和旋转,这三种
图形基本变换,图形在变换经过中, 发生了改变,
但变换前后的图形对应线段 ,对应角 ,它们
的 并没有改变。
位置
相等
相等
形状和大小
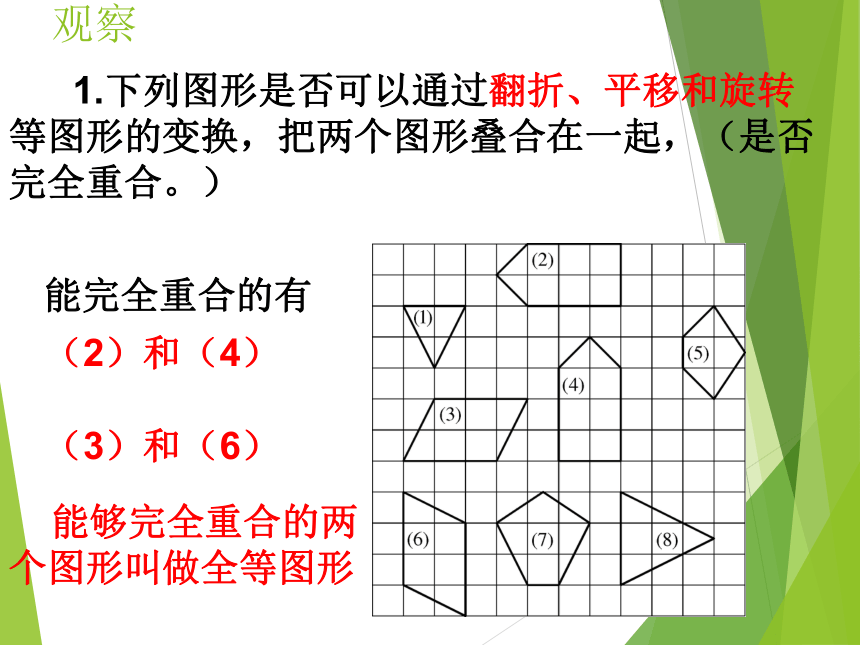
观察
1.下列图形是否可以通过翻折、平移和旋转
等图形的变换,把两个图形叠合在一起,(是否
完全重合。)
能够完全重合的两
个图形叫做全等图形
能完全重合的有
(3)和(6)
(2)和(4)
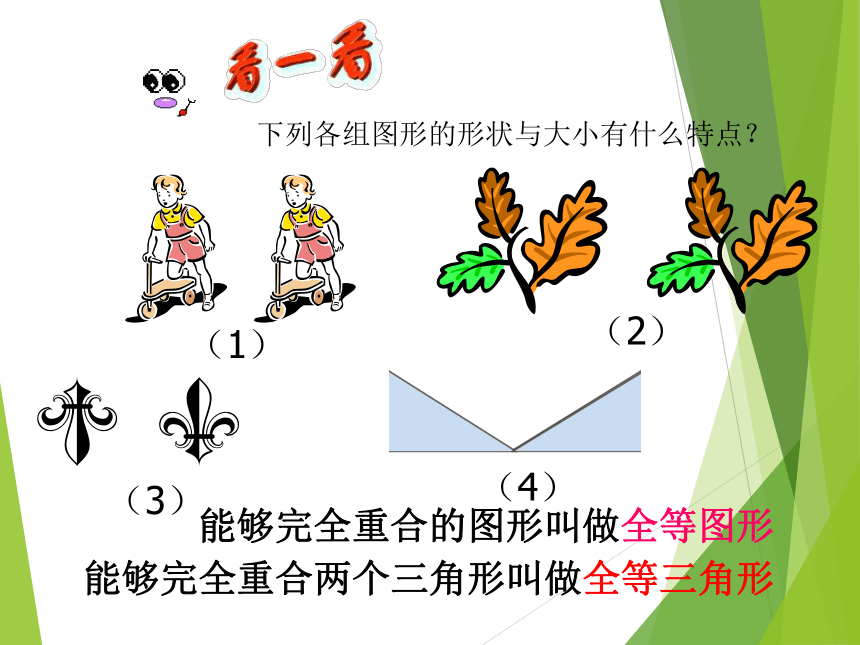
下列各组图形的形状与大小有什么特点?
能够完全重合的图形叫做全等图形
(1)
(2)
(3)
(4)
能够完全重合两个三角形叫做全等三角形
这两片叶子是全等形吗?
思考1.
一个图形经过翻折、平移和旋转等变换所得到
的新图形一定与原图形全等;反过来,两个全等的
图形经过上述变换后是否一定能够互相重合。
变换后一定能够互相重合。
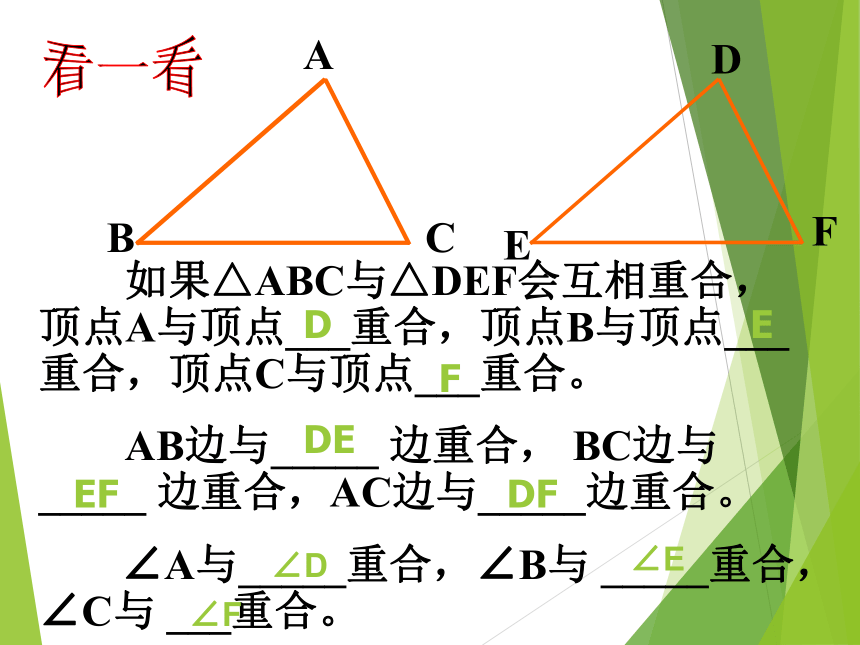
A
B
C
D
E
F
如果△ABC与△DEF会互相重合,顶点A与顶点___重合,顶点B与顶点___重合,顶点C与顶点___重合。
AB边与_____ 边重合, BC边与 _____ 边重合,AC边与_____边重合。
∠A与_____重合,∠B与 _____重合,∠C与 ___重合。
D
E
F
DE
EF
DF
∠D
∠E
∠F
两个全等三角形重合时,互相重合的顶点叫对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
“全等”用符号“≌ ”表示
记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
比如△ABC≌△DFE
A
D
B
F
C
E
读做“三角形ABC全等于三角形DEF”
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )
全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
思 考2.
1. 观察下图的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合
(1).多边形经过 变换而重
合,称为全等多边形.
(2).经过变换而重合,相互重合的顶点叫做
,相互重合的边叫做 ,相互重
合的角叫做 .
翻折、平移和旋转
对应顶点
对应边
对应角
A B
C D
B′
D′
A′ C′
A
B E
C D
A′
E′ B′
D′ C′
个全等的多边形表示方法
1.如图下中的两个五边形是全等的,记作
五边形ABCDE≌五边形A′B′C′D′E′
点A与 、点B与 、点C与 、点D与 。
点E与 分别是对应顶点.
这里,符号“≌”表示全等,读作“全等于”)。
A′
B′
C′
D′
E′
全等多边形的对应边、对应角分别相等.
2.这就是全等多边形的特征.
反过来边、角分别对应相等的两个多边形全等。
全等三角形
全等多边形的特征.
三角形是特殊的多边形,因此,全等三角形的
分别相等.同样,如果两个三角形
的 分别对应相等,那么这两个三角形全等.
对应边、对应角
边、角
1.如图 △ABC≌△DEF,且∠A=∠D,
∠B=∠E.你能指出它们之间其他的对应顶点、
对应角和对应边吗
对应顶点:
对应边:
对应角:
点A与D、
点B与E、
点C与F、
∠C=∠F
AB与DE
AC与DF
BC与EF
(1)是对应边相等、
( 2)对应角分别相等.
习题1. 图中所示的是两个全等的五边形,AB=8, AE=5, DE=11, HI=12, IJ=10, ∠C=90°, ∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的a、 b、 c、 d、 e、 α、 β各字母所表示的值.
E
A 5 11 D
8
B b
C
J
F
G I
H
e
115°
a
d
c
12
10
解:a=12、
α
b=10、
c=8、
d=5、
e=11、
α=90°、
β=115°.
2. 在下列方格图中画出两个全等的四边形和两个全等的三角形.
∴△EFG≌△E′F′G′
∴四边形ABCD≌四边形A′B′C′D′
A
B
D
C
C′
B′
D′
A′
G
G′
F′
E
E′
F
课堂小结
能够完全重合的图形叫做全等图形
能够完全重合的两个多边形叫做全等多边形
全等多边形的对应边相等,对应角相等。
边、角分别对应相等的两个多边形全等
图形的全等
我们已经认识了图形的翻折、平移和旋转,这三种
图形基本变换,图形在变换经过中, 发生了改变,
但变换前后的图形对应线段 ,对应角 ,它们
的 并没有改变。
位置
相等
相等
形状和大小
观察
1.下列图形是否可以通过翻折、平移和旋转
等图形的变换,把两个图形叠合在一起,(是否
完全重合。)
能够完全重合的两
个图形叫做全等图形
能完全重合的有
(3)和(6)
(2)和(4)
下列各组图形的形状与大小有什么特点?
能够完全重合的图形叫做全等图形
(1)
(2)
(3)
(4)
能够完全重合两个三角形叫做全等三角形
这两片叶子是全等形吗?
思考1.
一个图形经过翻折、平移和旋转等变换所得到
的新图形一定与原图形全等;反过来,两个全等的
图形经过上述变换后是否一定能够互相重合。
变换后一定能够互相重合。
A
B
C
D
E
F
如果△ABC与△DEF会互相重合,顶点A与顶点___重合,顶点B与顶点___重合,顶点C与顶点___重合。
AB边与_____ 边重合, BC边与 _____ 边重合,AC边与_____边重合。
∠A与_____重合,∠B与 _____重合,∠C与 ___重合。
D
E
F
DE
EF
DF
∠D
∠E
∠F
两个全等三角形重合时,互相重合的顶点叫对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
“全等”用符号“≌ ”表示
记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
比如△ABC≌△DFE
A
D
B
F
C
E
读做“三角形ABC全等于三角形DEF”
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )
全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
思 考2.
1. 观察下图的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合
(1).多边形经过 变换而重
合,称为全等多边形.
(2).经过变换而重合,相互重合的顶点叫做
,相互重合的边叫做 ,相互重
合的角叫做 .
翻折、平移和旋转
对应顶点
对应边
对应角
A B
C D
B′
D′
A′ C′
A
B E
C D
A′
E′ B′
D′ C′
个全等的多边形表示方法
1.如图下中的两个五边形是全等的,记作
五边形ABCDE≌五边形A′B′C′D′E′
点A与 、点B与 、点C与 、点D与 。
点E与 分别是对应顶点.
这里,符号“≌”表示全等,读作“全等于”)。
A′
B′
C′
D′
E′
全等多边形的对应边、对应角分别相等.
2.这就是全等多边形的特征.
反过来边、角分别对应相等的两个多边形全等。
全等三角形
全等多边形的特征.
三角形是特殊的多边形,因此,全等三角形的
分别相等.同样,如果两个三角形
的 分别对应相等,那么这两个三角形全等.
对应边、对应角
边、角
1.如图 △ABC≌△DEF,且∠A=∠D,
∠B=∠E.你能指出它们之间其他的对应顶点、
对应角和对应边吗
对应顶点:
对应边:
对应角:
点A与D、
点B与E、
点C与F、
∠C=∠F
AB与DE
AC与DF
BC与EF
(1)是对应边相等、
( 2)对应角分别相等.
习题1. 图中所示的是两个全等的五边形,AB=8, AE=5, DE=11, HI=12, IJ=10, ∠C=90°, ∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的a、 b、 c、 d、 e、 α、 β各字母所表示的值.
E
A 5 11 D
8
B b
C
J
F
G I
H
e
115°
a
d
c
12
10
解:a=12、
α
b=10、
c=8、
d=5、
e=11、
α=90°、
β=115°.
2. 在下列方格图中画出两个全等的四边形和两个全等的三角形.
∴△EFG≌△E′F′G′
∴四边形ABCD≌四边形A′B′C′D′
A
B
D
C
C′
B′
D′
A′
G
G′
F′
E
E′
F
课堂小结
能够完全重合的图形叫做全等图形
能够完全重合的两个多边形叫做全等多边形
全等多边形的对应边相等,对应角相等。
边、角分别对应相等的两个多边形全等
