冀教版七年级数学下册7.2.2 相交线 课件(共27张PPT)
文档属性
| 名称 | 冀教版七年级数学下册7.2.2 相交线 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
7.2.2相交线
学习目标
1
2
3
理解垂线,垂线段的概念.
掌握垂直的概念,能根据垂直求出角的度数,
理解点到直线的距离的概念,并会度量点到直线的距离.
掌握垂线的性质,并会利用所学知识进行简单的推理.
掌握垂线段最短的性质,并会利用所学知识解决简单的实际问题.
学习重难点
重点
难点
掌握垂线、点到直线的距离的概念.
掌握有关垂线的一个基本事实及直线外的一点与直线上各点的连接的所有线段中,垂线段最短.
问题导入
在奥运会的跳远比赛中,裁判员在测量运动员的跳远成绩时,拉紧的皮尺与起跳线有什么关系?这样做的依据是什么?
探究新知
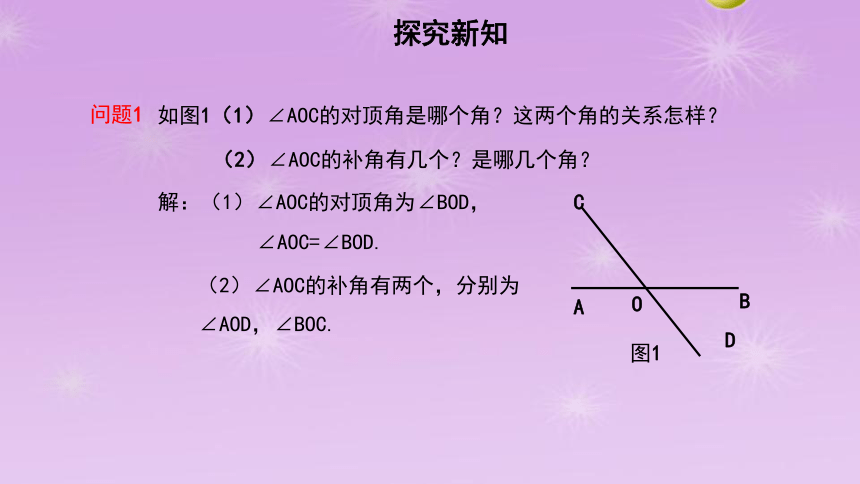
如图1(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的补角有几个?是哪几个角?
A
B
C
D
O
图1
解:(1)∠AOC的对顶角为∠BOD,
∠AOC=∠BOD.
(2)∠AOC的补角有两个,分别为
∠AOD,∠BOC.
问题1
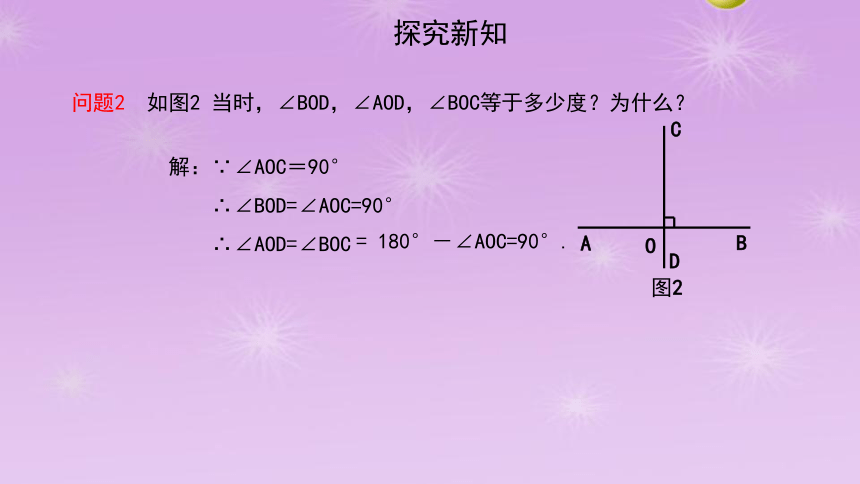
问题2 如图2 当时,∠BOD,∠AOD,∠BOC等于多少度?为什么?
A
B
C
D
O
图2
解:∵∠AOC=90°
∴∠BOD=∠AOC=90°
∴∠AOD=∠BOC
探究新知
= 180°-∠AOC=90°.
定义 当两条直线所成的四个角中有一个角是直角时,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.它们的交点叫做垂足.
归纳
文字语言:直线AB与CD相交于点O,当∠BOC=90°,称直线AB与CD互相垂直,O为垂足.
A
B
C
D
O
图2
含义2:∵AB⊥CD,∴∠BOC=90°.
含义1:∵∠BOC=90°,
垂直用符号 “⊥”来表示,读作“垂直于”
几何语言:∠BOC=90°,AB⊥CD,O为垂足.
垂直
归纳
∴AB⊥CD.
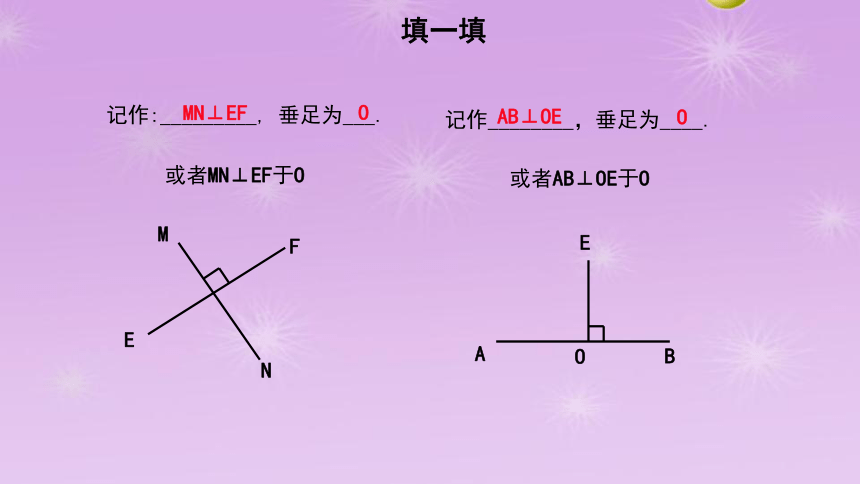
记作:_________, 垂足为___.
记作________,垂足为____.
或者MN⊥EF于O
或者AB⊥OE于O
F
E
N
M
A
B
O
E
MN⊥EF
O
AB⊥OE
O
填一填
L
A
1.贴
如图,过直线 L 上的一点A ,作L的垂线.
问题:这样画l的垂线可以画几条?
一条
2.过
3.画
动手探究
提示:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:
归纳
F
如图,已知直线AB、线段CD和点E,过点E分别画出直线AB、线段CD的垂线。
E
A
B
C
D
注:画一条线段或射线的垂线,就是画它们所在的直线的垂线。
练一练
你能借助三角尺或量角器经过直线AB外的一点P画出AB的垂线吗?.
P
Q
∴ PQ为所求
∴ PQ为所求
动手操作
A
B
A
B
画垂线的方法可归纳为“一落、二过、三画”
1.一落:把三角尺的一条直角边落在已知直线上;
2.二过:让三角尺的另一条直角边经过已知的点;
3.三画:沿着直角边经过已知点画直线.
A
B
P
方法归纳
有人不慎掉入有鳄鱼的湖中.如图,他在P点,应选择什么样的路线尽快游到岸边m呢?
思考
连接直线外一点与直线上各点的所有线段中,垂线段最短.
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线的性质2
垂线段
斜线段
∵PB⊥m于B,
∴PB归纳
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
垂线
垂线段
归纳
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
m
A
例如:如图,PA⊥m于点A ,垂线段PA的长度叫做点P到直线m的距离.
点到直线的距离的概念:
探究
已知直线L外一点P,则点P到直线L的距离是指( )
(A)点P到直线L的垂线的长度
(B)点P到直线L的垂线
(C)点P到直线L的垂线段的长度
(D)点P到直线L的垂线段
C
练一练
点到直线的距离是垂线段的长度,是一个数值,而垂线段是一个图形,对此要分清楚.
注意:
1.下面四种判定两条直线垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
A. 4 B. 3 C. 2 D. 1
A
b
a
练一练
2.如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB
C.线段PC D.线段PD
3.如图,下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
B
D
练一练
4.如图,已知直线AB,CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是 .
C
A
B
O
E
1
2
OE⊥AB
5.如图,三条直线AB,CD和EF相交于点O,∠AOE=40°,
∠BOD=50°,则图中互相垂直的两条直线是________.
EF和CD
练一练
6.如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小.
解:∵ AC⊥BC于C (已知),
∴ AC<AB(垂线的性质二) .
又∵ CD⊥AD于D(已知),
∴ CD<AC(垂线的性质二).
∵ DE⊥CE于E(已知),
∴ DE<CD(垂线的性质二).
∴ AB>AC>CD>DE.
练一练
课堂小结
垂线
定义
基本事实
点到直线的距离
直线AB与CD相交于点O,若∠BOC=90°,则AB⊥CD,O为垂足.
经过直线上或直线外的一点,有且只有一条直线与已知直线垂直.
直线外的一点与直线上各点连接的所有线段中,垂线段最短.
垂线段CO的长度叫做点C到直线AB的距离.
课后作业
过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
D
课后作业
再见
7.2.2相交线
学习目标
1
2
3
理解垂线,垂线段的概念.
掌握垂直的概念,能根据垂直求出角的度数,
理解点到直线的距离的概念,并会度量点到直线的距离.
掌握垂线的性质,并会利用所学知识进行简单的推理.
掌握垂线段最短的性质,并会利用所学知识解决简单的实际问题.
学习重难点
重点
难点
掌握垂线、点到直线的距离的概念.
掌握有关垂线的一个基本事实及直线外的一点与直线上各点的连接的所有线段中,垂线段最短.
问题导入
在奥运会的跳远比赛中,裁判员在测量运动员的跳远成绩时,拉紧的皮尺与起跳线有什么关系?这样做的依据是什么?
探究新知
如图1(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的补角有几个?是哪几个角?
A
B
C
D
O
图1
解:(1)∠AOC的对顶角为∠BOD,
∠AOC=∠BOD.
(2)∠AOC的补角有两个,分别为
∠AOD,∠BOC.
问题1
问题2 如图2 当时,∠BOD,∠AOD,∠BOC等于多少度?为什么?
A
B
C
D
O
图2
解:∵∠AOC=90°
∴∠BOD=∠AOC=90°
∴∠AOD=∠BOC
探究新知
= 180°-∠AOC=90°.
定义 当两条直线所成的四个角中有一个角是直角时,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.它们的交点叫做垂足.
归纳
文字语言:直线AB与CD相交于点O,当∠BOC=90°,称直线AB与CD互相垂直,O为垂足.
A
B
C
D
O
图2
含义2:∵AB⊥CD,∴∠BOC=90°.
含义1:∵∠BOC=90°,
垂直用符号 “⊥”来表示,读作“垂直于”
几何语言:∠BOC=90°,AB⊥CD,O为垂足.
垂直
归纳
∴AB⊥CD.
记作:_________, 垂足为___.
记作________,垂足为____.
或者MN⊥EF于O
或者AB⊥OE于O
F
E
N
M
A
B
O
E
MN⊥EF
O
AB⊥OE
O
填一填
L
A
1.贴
如图,过直线 L 上的一点A ,作L的垂线.
问题:这样画l的垂线可以画几条?
一条
2.过
3.画
动手探究
提示:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:
归纳
F
如图,已知直线AB、线段CD和点E,过点E分别画出直线AB、线段CD的垂线。
E
A
B
C
D
注:画一条线段或射线的垂线,就是画它们所在的直线的垂线。
练一练
你能借助三角尺或量角器经过直线AB外的一点P画出AB的垂线吗?.
P
Q
∴ PQ为所求
∴ PQ为所求
动手操作
A
B
A
B
画垂线的方法可归纳为“一落、二过、三画”
1.一落:把三角尺的一条直角边落在已知直线上;
2.二过:让三角尺的另一条直角边经过已知的点;
3.三画:沿着直角边经过已知点画直线.
A
B
P
方法归纳
有人不慎掉入有鳄鱼的湖中.如图,他在P点,应选择什么样的路线尽快游到岸边m呢?
思考
连接直线外一点与直线上各点的所有线段中,垂线段最短.
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线的性质2
垂线段
斜线段
∵PB⊥m于B,
∴PB
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
垂线
垂线段
归纳
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
m
A
例如:如图,PA⊥m于点A ,垂线段PA的长度叫做点P到直线m的距离.
点到直线的距离的概念:
探究
已知直线L外一点P,则点P到直线L的距离是指( )
(A)点P到直线L的垂线的长度
(B)点P到直线L的垂线
(C)点P到直线L的垂线段的长度
(D)点P到直线L的垂线段
C
练一练
点到直线的距离是垂线段的长度,是一个数值,而垂线段是一个图形,对此要分清楚.
注意:
1.下面四种判定两条直线垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
A. 4 B. 3 C. 2 D. 1
A
b
a
练一练
2.如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB
C.线段PC D.线段PD
3.如图,下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
B
D
练一练
4.如图,已知直线AB,CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是 .
C
A
B
O
E
1
2
OE⊥AB
5.如图,三条直线AB,CD和EF相交于点O,∠AOE=40°,
∠BOD=50°,则图中互相垂直的两条直线是________.
EF和CD
练一练
6.如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小.
解:∵ AC⊥BC于C (已知),
∴ AC<AB(垂线的性质二) .
又∵ CD⊥AD于D(已知),
∴ CD<AC(垂线的性质二).
∵ DE⊥CE于E(已知),
∴ DE<CD(垂线的性质二).
∴ AB>AC>CD>DE.
练一练
课堂小结
垂线
定义
基本事实
点到直线的距离
直线AB与CD相交于点O,若∠BOC=90°,则AB⊥CD,O为垂足.
经过直线上或直线外的一点,有且只有一条直线与已知直线垂直.
直线外的一点与直线上各点连接的所有线段中,垂线段最短.
垂线段CO的长度叫做点C到直线AB的距离.
课后作业
过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
D
课后作业
再见
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
