冀教版七年级数学下册7.4 平行线的判定 课件(共23张PPT)
文档属性
| 名称 | 冀教版七年级数学下册7.4 平行线的判定 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
7.4平行线的判定
理解掌握平行线的判定定理.
能熟练运用平行线的判定定理判定两条直线是否平行.
经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力.
学习目标
1
2
3
理解掌握平行线的判定定理.
能熟练运用平行线的判定定理判定两条直线是否平行.
学习重难点
重点:
难点:
复习导入
买2瓶苹果汁的钱比买3瓶橙汁的钱少2块.
A
B
C
D
E
F
1
2
3
4
问题1 如图,图中∠2的同位角是______,内错角是_______,同旁内角是_______.
问题2 若∠2=∠3,则直线AB与CD有怎样的位置关系?为什么?
∠3
∠1
∠4
AB∥CD
同位角相等,两直线平行.
情境导入
装修工人正在向墙上钉木条,如果木条b与墙壁的边缘垂直,那么木条a与墙壁的边缘所夹的角为多少度时,才能使木条a与木条b平行?
探究
5瓶苹果汁价钱+3瓶橙汁价钱=16元
2瓶苹果汁价钱-3瓶橙汁的价钱=-2元
如图,直线AB,CD与直线EF相交,若∠2=∠3,试判断直线AB,CD的位置关系.
A
B
C
D
E
F
1
2
3
4
∵∠2=∠3∴AB∥CD(同位角相等,两直线平行).
还有没有别的办法判定直线AB与CD的位置关系呢?
探究
∵∠1=∠3(对顶角相等),若∠1=∠2,那么就能推出∠2=∠3,于是就有AB∥CD.
∵∠3+∠4=180°(平角定义),如果∠2+∠4=180°,那么就能推出∠2=∠3,于是就有AB∥CD.
他们的想法正确吗?
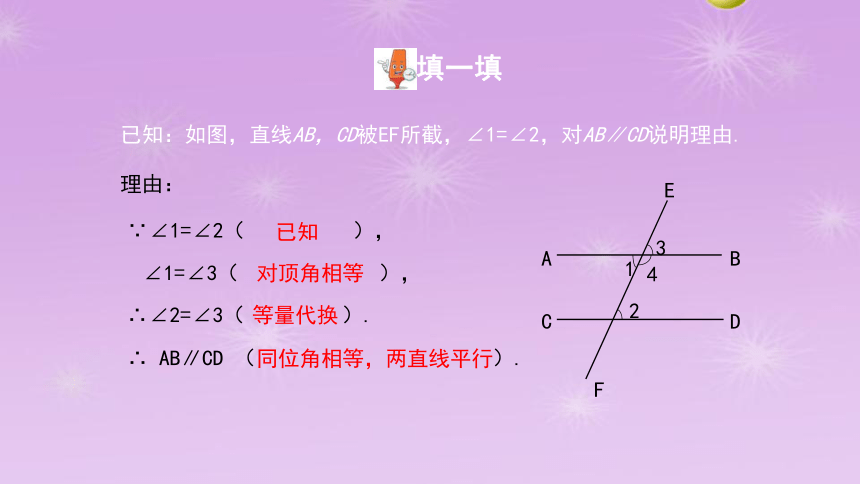
填一填
已知:如图,直线AB,CD被EF所截,∠1=∠2,对AB∥CD说明理由.
A
B
C
D
E
F
1
2
3
4
理由:
∵∠1=∠2( ),
∠1=∠3( ),
∴∠2=∠3( ).
∴ AB∥CD ( ).
已知
对顶角相等
等量代换
同位角相等,两直线平行
归纳总结
我们能得到什么结论?
两条直线被第三条直线所截,如果内错角相等, 那么这两条直线平行
已知:如图,直线AB,CD被EF所截,∠4+∠2=180°,对AB∥CD说明理由.
A
B
C
D
E
F
1
2
3
4
理由:
∵∠4+∠2=180°( ),
∠4+∠3=180°( ),
∴ ∠2=180°-∠4,∠3=180°-∠4
( ).
∴ AB∥CD ( ).
已知
平角定义
同位角相等,两直线平行
等式的性质
∴ ∠2=∠3( ).
等量代换
试一试
我们能得到什么结论?
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
归纳总结
知识要点
1
2
3
平行四边形的判定定理.
内错角相等, 两直线平行.
同旁内角互补,两直线平行.
例题解析
A
B
C
D
E
F
1
2
3
4
∴ ∠1+∠4=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
例1 已知:如图直线AB,CD被直线EF所截,∠1=60°,∠2=120°.
对AB∥CD说明理由.
理由:
∵∠1+∠2=60°+120°=180°(已知),
∠2=∠4 ,
方法总结
推理说明时,要符合一定的逻辑顺序,因果关系,即由什么条件,根据什么理论,得出什么结果.
练习
1.如图,已知∠1=30°,∠2或 ∠3满足条件___________________ ,则a//b.
2
1
3
a
b
c
∠2=150 或∠3=30°
°
解:AB//CD,AD//BC.
理由:
D
C
B
A
2.如图:已知 B= D=45°, C=135°,问图中有哪些直线平行?
练习
∴ AB//CD,AD//BC(同旁内角互补,两直线平行)
∵ B=∠D=45°,
C=135°(已知)
∴ B+ C=180°,
∠D+∠C=180°.(等式的性质)
课堂练习
1.如图,不能判定 的是 ( )
A.∠2=∠3 B.∠1=∠4
C.∠1=∠2 D.∠1=∠3
D
2. 如图,∠1=∠2,则下列结论正确的是( )
C
A. AD//BC B.AB//CD
C. AD//EF D.EF//BC
课堂练习
C
1
2
3
A
E
B
D
C
3.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B.∠1=∠A
C.∠3=∠B
D.∠3=∠A
课堂练习
(1)(2)(4)
4
8
6
2
1
5
3
7
a
b
c
4.直线a,b被直线c所截,给出下列条件:
(1)∠1=∠2;(2)∠3=∠6;(3)∠4=∠1;(4)∠6+∠7=180°.
其中能判定a∥b的条件序号是.
课堂练习
5.如图, ∠B=∠C, ∠B+∠D=180°,那么BC平行DE吗?为什么?
A
B
C
D
E
解:BC∥DE.
理由如下:
∵ ∠B=∠C ( ),
已知
∠B+∠D=180°( ),
已知
∴ ∠C+∠D=180°
(等量代换),
∴BC∥DE( .
同旁内角互补,两直线平行 )
课堂练习
6.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
Q
解: AB∥CD,理由如下:
过点F向左作FQ,使∠MFQ=∠2=50°,
则AB∥FQ,∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
∵AB∥FQ,∠1=140°,
∴∠1+∠NFQ=180°,
∴CD∥FQ,∴AB∥CD.
总结
判定两条直线平行的方法
文字叙述 符号语言 图形
同位角
内错角
同旁内角
∵∠1=∠2(已知),
∴a∥b.
a
b
c
1
2
3
4
∵∠3=∠2(已知),
∴a∥b.
∵∠4+∠2=180°(已知),∴a∥b.
相等
两直线平行
相等
两直线平行
互补
两直线平行
谢谢听讲!
7.4平行线的判定
理解掌握平行线的判定定理.
能熟练运用平行线的判定定理判定两条直线是否平行.
经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力.
学习目标
1
2
3
理解掌握平行线的判定定理.
能熟练运用平行线的判定定理判定两条直线是否平行.
学习重难点
重点:
难点:
复习导入
买2瓶苹果汁的钱比买3瓶橙汁的钱少2块.
A
B
C
D
E
F
1
2
3
4
问题1 如图,图中∠2的同位角是______,内错角是_______,同旁内角是_______.
问题2 若∠2=∠3,则直线AB与CD有怎样的位置关系?为什么?
∠3
∠1
∠4
AB∥CD
同位角相等,两直线平行.
情境导入
装修工人正在向墙上钉木条,如果木条b与墙壁的边缘垂直,那么木条a与墙壁的边缘所夹的角为多少度时,才能使木条a与木条b平行?
探究
5瓶苹果汁价钱+3瓶橙汁价钱=16元
2瓶苹果汁价钱-3瓶橙汁的价钱=-2元
如图,直线AB,CD与直线EF相交,若∠2=∠3,试判断直线AB,CD的位置关系.
A
B
C
D
E
F
1
2
3
4
∵∠2=∠3∴AB∥CD(同位角相等,两直线平行).
还有没有别的办法判定直线AB与CD的位置关系呢?
探究
∵∠1=∠3(对顶角相等),若∠1=∠2,那么就能推出∠2=∠3,于是就有AB∥CD.
∵∠3+∠4=180°(平角定义),如果∠2+∠4=180°,那么就能推出∠2=∠3,于是就有AB∥CD.
他们的想法正确吗?
填一填
已知:如图,直线AB,CD被EF所截,∠1=∠2,对AB∥CD说明理由.
A
B
C
D
E
F
1
2
3
4
理由:
∵∠1=∠2( ),
∠1=∠3( ),
∴∠2=∠3( ).
∴ AB∥CD ( ).
已知
对顶角相等
等量代换
同位角相等,两直线平行
归纳总结
我们能得到什么结论?
两条直线被第三条直线所截,如果内错角相等, 那么这两条直线平行
已知:如图,直线AB,CD被EF所截,∠4+∠2=180°,对AB∥CD说明理由.
A
B
C
D
E
F
1
2
3
4
理由:
∵∠4+∠2=180°( ),
∠4+∠3=180°( ),
∴ ∠2=180°-∠4,∠3=180°-∠4
( ).
∴ AB∥CD ( ).
已知
平角定义
同位角相等,两直线平行
等式的性质
∴ ∠2=∠3( ).
等量代换
试一试
我们能得到什么结论?
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
归纳总结
知识要点
1
2
3
平行四边形的判定定理.
内错角相等, 两直线平行.
同旁内角互补,两直线平行.
例题解析
A
B
C
D
E
F
1
2
3
4
∴ ∠1+∠4=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
例1 已知:如图直线AB,CD被直线EF所截,∠1=60°,∠2=120°.
对AB∥CD说明理由.
理由:
∵∠1+∠2=60°+120°=180°(已知),
∠2=∠4 ,
方法总结
推理说明时,要符合一定的逻辑顺序,因果关系,即由什么条件,根据什么理论,得出什么结果.
练习
1.如图,已知∠1=30°,∠2或 ∠3满足条件___________________ ,则a//b.
2
1
3
a
b
c
∠2=150 或∠3=30°
°
解:AB//CD,AD//BC.
理由:
D
C
B
A
2.如图:已知 B= D=45°, C=135°,问图中有哪些直线平行?
练习
∴ AB//CD,AD//BC(同旁内角互补,两直线平行)
∵ B=∠D=45°,
C=135°(已知)
∴ B+ C=180°,
∠D+∠C=180°.(等式的性质)
课堂练习
1.如图,不能判定 的是 ( )
A.∠2=∠3 B.∠1=∠4
C.∠1=∠2 D.∠1=∠3
D
2. 如图,∠1=∠2,则下列结论正确的是( )
C
A. AD//BC B.AB//CD
C. AD//EF D.EF//BC
课堂练习
C
1
2
3
A
E
B
D
C
3.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B.∠1=∠A
C.∠3=∠B
D.∠3=∠A
课堂练习
(1)(2)(4)
4
8
6
2
1
5
3
7
a
b
c
4.直线a,b被直线c所截,给出下列条件:
(1)∠1=∠2;(2)∠3=∠6;(3)∠4=∠1;(4)∠6+∠7=180°.
其中能判定a∥b的条件序号是.
课堂练习
5.如图, ∠B=∠C, ∠B+∠D=180°,那么BC平行DE吗?为什么?
A
B
C
D
E
解:BC∥DE.
理由如下:
∵ ∠B=∠C ( ),
已知
∠B+∠D=180°( ),
已知
∴ ∠C+∠D=180°
(等量代换),
∴BC∥DE( .
同旁内角互补,两直线平行 )
课堂练习
6.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
Q
解: AB∥CD,理由如下:
过点F向左作FQ,使∠MFQ=∠2=50°,
则AB∥FQ,∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
∵AB∥FQ,∠1=140°,
∴∠1+∠NFQ=180°,
∴CD∥FQ,∴AB∥CD.
总结
判定两条直线平行的方法
文字叙述 符号语言 图形
同位角
内错角
同旁内角
∵∠1=∠2(已知),
∴a∥b.
a
b
c
1
2
3
4
∵∠3=∠2(已知),
∴a∥b.
∵∠4+∠2=180°(已知),∴a∥b.
相等
两直线平行
相等
两直线平行
互补
两直线平行
谢谢听讲!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
