华东师大版七年级下册数学 9.1 三角形外角性质 课件(共19张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.1 三角形外角性质 课件(共19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 11:47:19 | ||
图片预览



文档简介
(共19张PPT)
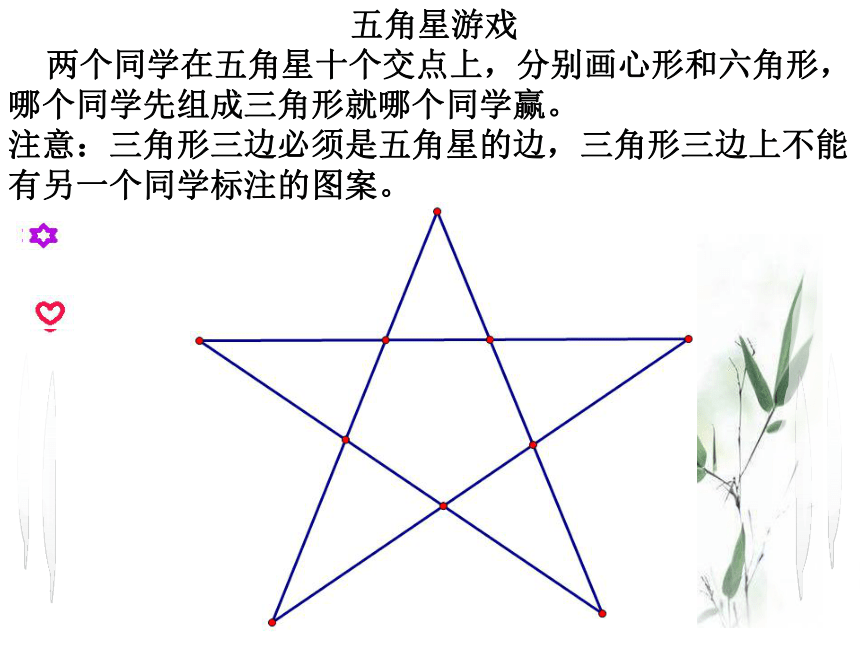
五角星游戏
两个同学在五角星十个交点上,分别画心形和六角形,哪个同学先组成三角形就哪个同学赢。
注意:三角形三边必须是五角星的边,三角形三边上不能有另一个同学标注的图案。
A
B
C
D
E
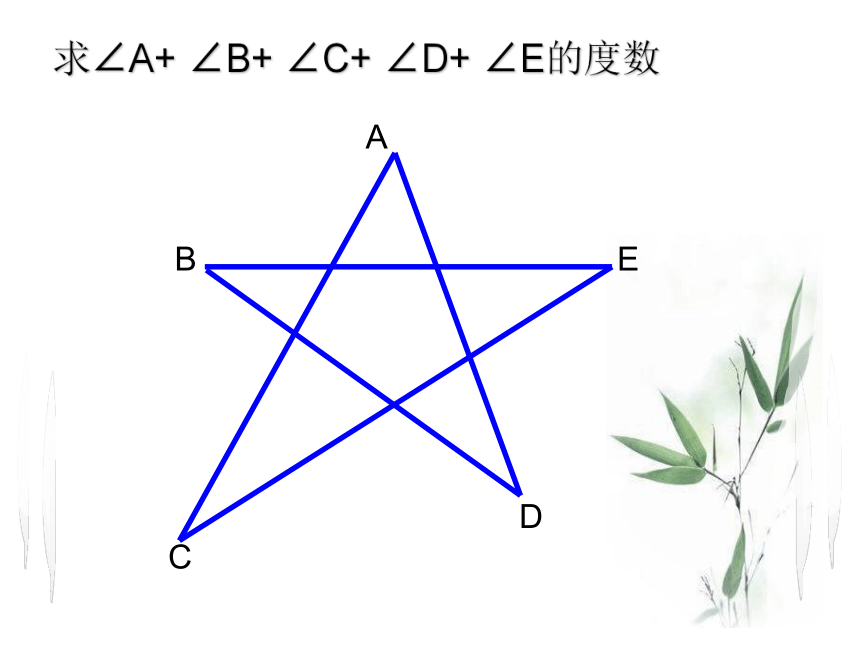
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
C
A
B
D
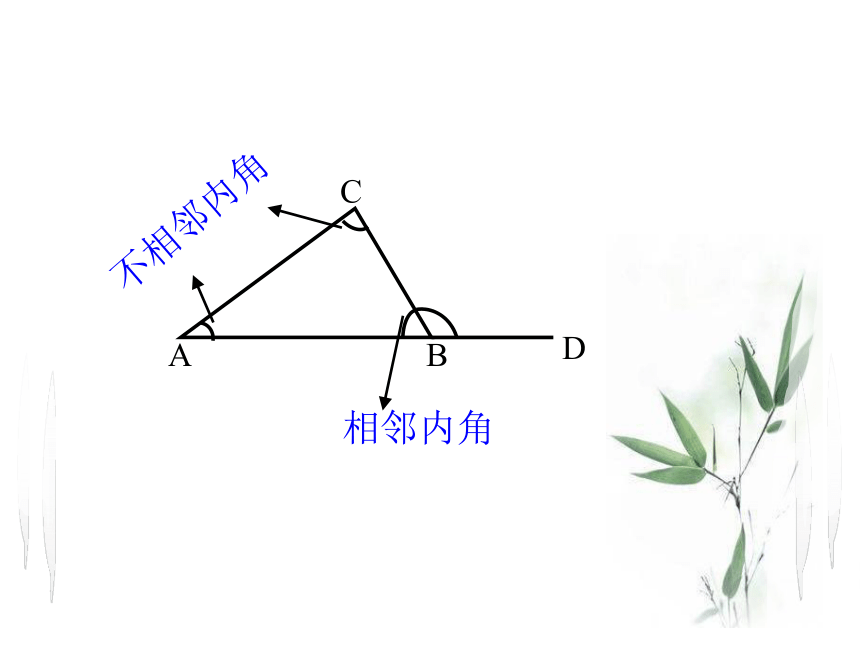
相邻内角
不相邻内角
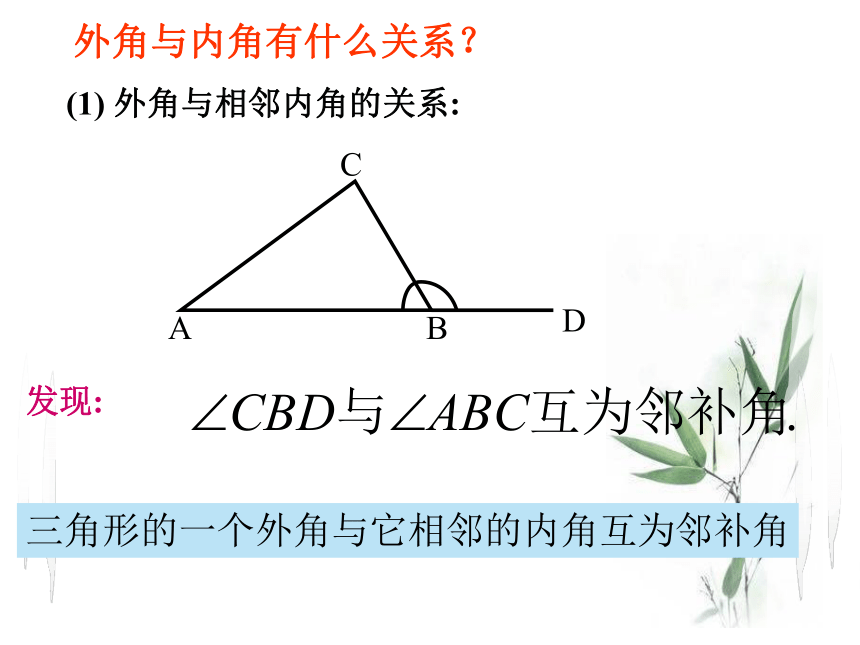
外角与内角有什么关系?
(1) 外角与相邻内角的关系:
C
A
B
D
发现:
三角形的一个外角与它相邻的内角互为邻补角
下面探索三角形的一个外角与它不相邻的两个内角间关系。
做一做
把∠A与∠C剪下来,
让∠A与∠C顶点重合,拼在一起
把组成的新的角放到∠CBD上,使角的顶点重合,
看看会出现什么样的结果?
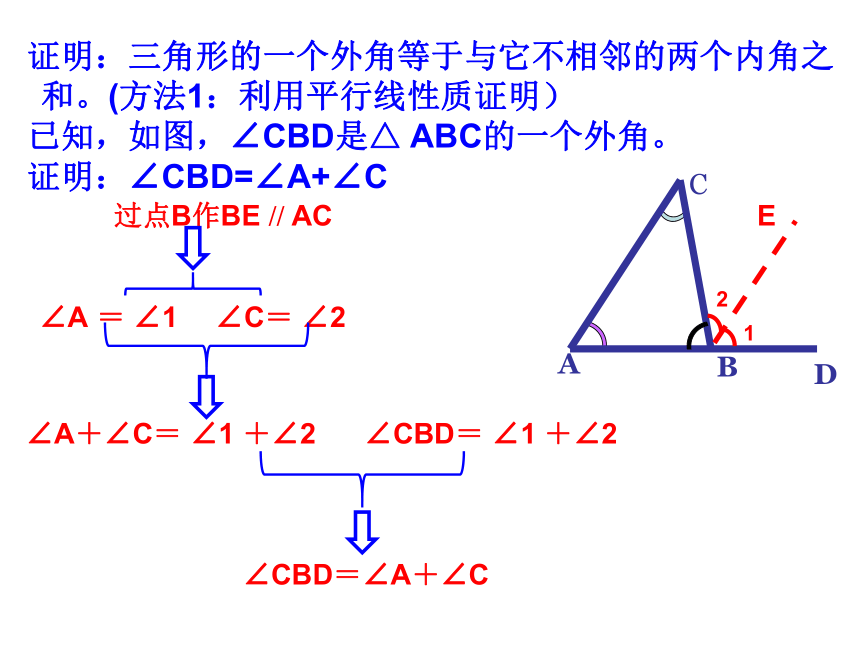
证明:三角形的一个外角等于与它不相邻的两个内角之和。(方法1:利用平行线性质证明)
已知,如图,∠CBD是△ ABC的一个外角。
证明:∠CBD=∠A+∠C
C
B
A
D
2
1
E
过点B作BE // AC
∠A = ∠1
∠C= ∠2
∠A+∠C= ∠1 +∠2
∠CBD= ∠1 +∠2
∠CBD=∠A+∠C
证明:三角形的一个外角等于与它不相邻的两个
内角之和。(方法2:利用三角形的内角和证明)
已知,如图,∠CBD是△ ABC的一个外角。
证明:∠CBD=∠A+∠C
C
A
B
D
三角形内角和是180°
∠A+∠C+∠ABC=180°
∠CBD与∠ABC互为邻补角
∠CBD+∠ABC =180°
∠CBD=∠A + ∠C
C
A
B
D
证明:三角形的一个外角等于与它不相邻的两个
内角之和。(方法2:利用三角形的内角和证明)
已知,如图,∠CBD是△ ABC的一个外角。
证明:∠CBD=∠A+∠C
∠CBD+∠ABC =180°(邻补角的定义)
∠A+∠C+∠ABC=180°(三角形内角和是180°)
∠CBD=180°-∠ABC
∠A+∠C=180°-∠ABC
∠CBD=∠A+∠C(等量代换)
三角形的一个外角等于与它不相邻的两个内角之和
三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢?
C
A
B
D
∠CBD=∠A + ∠C
∠CBD>∠A
∠CBD>∠C
三角形的一个外角大于任何一个与它不相邻的内角。
(3)三角形的一个外角大于任何一个与它不相邻的内角。
结论
(1)三角形的一个外角与它相邻的内角互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
练习1 判断题
1、三角形的一个外角等于两个内角的和。( )
2、三角形的一个外角等于与它不相邻的两个内角的和。( )
3、三角形的一个外角大于任何一个内角。( )
4、三角形的一个外角大于任何一个与它不相邻的内角。( )
35°
120°
1
45°
50°
1
∠1=
∠1=
85
95
练习2
说出下列各图中∠1的度数.
1
60°
55°
练习2 说出各图中∠1的度数
100 o
60 o
1
∠1=
115
∠1=
40
>
>
∠5
∠C
∠3
∠B
______+______
______+______
A
B
D
C
____
____
1
2
3
5
∠1=
∠3
∠2
∠2
∠B
∠2=
练习3 根据三角形外角性质填空
∠1是
的外角
∠2是
的外角
△ADC
△ABD
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
F
G
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
⌒
F
G
⌒
∵ ∠2 是△BDG的外角
∴ ∠1 =∠A+ ∠C
解:∵∠1 是△ACF的外角
∴∠A+ ∠B+ ∠C+ ∠D+ ∠E=
∴ ∠2 =∠B+ ∠D
(∠A+ ∠C)+ (∠B+ ∠D)+ ∠E=
∠1 + ∠2 + ∠E =
180°
1
2
五角星游戏
两个同学在五角星十个交点上,分别画心形和六角形,哪个同学先组成三角形就哪个同学赢。
注意:三角形三边必须是五角星的边,三角形三边上不能有另一个同学标注的图案。
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
C
A
B
D
相邻内角
不相邻内角
外角与内角有什么关系?
(1) 外角与相邻内角的关系:
C
A
B
D
发现:
三角形的一个外角与它相邻的内角互为邻补角
下面探索三角形的一个外角与它不相邻的两个内角间关系。
做一做
把∠A与∠C剪下来,
让∠A与∠C顶点重合,拼在一起
把组成的新的角放到∠CBD上,使角的顶点重合,
看看会出现什么样的结果?
证明:三角形的一个外角等于与它不相邻的两个内角之和。(方法1:利用平行线性质证明)
已知,如图,∠CBD是△ ABC的一个外角。
证明:∠CBD=∠A+∠C
C
B
A
D
2
1
E
过点B作BE // AC
∠A = ∠1
∠C= ∠2
∠A+∠C= ∠1 +∠2
∠CBD= ∠1 +∠2
∠CBD=∠A+∠C
证明:三角形的一个外角等于与它不相邻的两个
内角之和。(方法2:利用三角形的内角和证明)
已知,如图,∠CBD是△ ABC的一个外角。
证明:∠CBD=∠A+∠C
C
A
B
D
三角形内角和是180°
∠A+∠C+∠ABC=180°
∠CBD与∠ABC互为邻补角
∠CBD+∠ABC =180°
∠CBD=∠A + ∠C
C
A
B
D
证明:三角形的一个外角等于与它不相邻的两个
内角之和。(方法2:利用三角形的内角和证明)
已知,如图,∠CBD是△ ABC的一个外角。
证明:∠CBD=∠A+∠C
∠CBD+∠ABC =180°(邻补角的定义)
∠A+∠C+∠ABC=180°(三角形内角和是180°)
∠CBD=180°-∠ABC
∠A+∠C=180°-∠ABC
∠CBD=∠A+∠C(等量代换)
三角形的一个外角等于与它不相邻的两个内角之和
三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢?
C
A
B
D
∠CBD=∠A + ∠C
∠CBD>∠A
∠CBD>∠C
三角形的一个外角大于任何一个与它不相邻的内角。
(3)三角形的一个外角大于任何一个与它不相邻的内角。
结论
(1)三角形的一个外角与它相邻的内角互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
练习1 判断题
1、三角形的一个外角等于两个内角的和。( )
2、三角形的一个外角等于与它不相邻的两个内角的和。( )
3、三角形的一个外角大于任何一个内角。( )
4、三角形的一个外角大于任何一个与它不相邻的内角。( )
35°
120°
1
45°
50°
1
∠1=
∠1=
85
95
练习2
说出下列各图中∠1的度数.
1
60°
55°
练习2 说出各图中∠1的度数
100 o
60 o
1
∠1=
115
∠1=
40
>
>
∠5
∠C
∠3
∠B
______+______
______+______
A
B
D
C
____
____
1
2
3
5
∠1=
∠3
∠2
∠2
∠B
∠2=
练习3 根据三角形外角性质填空
∠1是
的外角
∠2是
的外角
△ADC
△ABD
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
F
G
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
⌒
F
G
⌒
∵ ∠2 是△BDG的外角
∴ ∠1 =∠A+ ∠C
解:∵∠1 是△ACF的外角
∴∠A+ ∠B+ ∠C+ ∠D+ ∠E=
∴ ∠2 =∠B+ ∠D
(∠A+ ∠C)+ (∠B+ ∠D)+ ∠E=
∠1 + ∠2 + ∠E =
180°
1
2
