华东师大版八年级数学下册:17.2.1 平面直角坐标系 课件(共21张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册:17.2.1 平面直角坐标系 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 12:42:43 | ||
图片预览






文档简介
(共21张PPT)
17.2 函数的图象
1 平面直角坐标系
华师大版八年级数学(下)
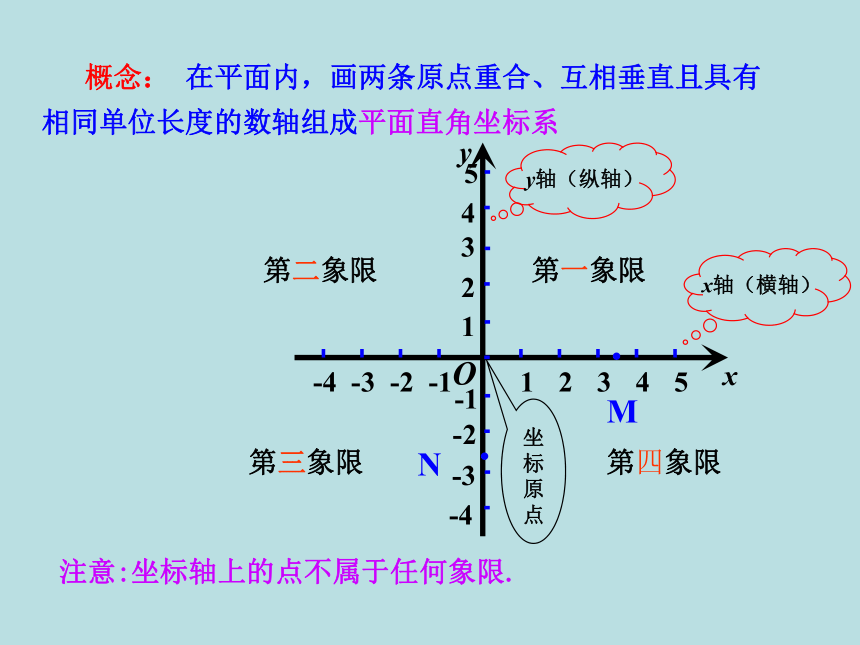
概念: 在平面内,画两条原点重合、互相垂直且具有相同单位长度的数轴组成平面直角坐标系
y轴(纵轴)
x轴(横轴)
坐标原点
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
·
M
N ·
(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度相同
说一说:平面直角坐标系中两条数轴具有哪些特征呢?
-4 -3 -2 -1 1 2 3 4
O
x
y
4
3
2
1
-1
-2
-3
-4
·
A
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x轴上的坐标为4
A点在y轴上的坐标为2
A点在平面直角坐标系中的
坐标为(4, 2)记作:A(4,2)
x轴上的坐标
写在前面
·
B
(-4, 1)
o
y
(a,b)
b
a
对于平面内任意一点A,
过点A分别作x轴,y轴的
垂线,垂足在x轴,y轴上对应的数a,b分别叫做点A
的横坐标、纵坐标,有序
实数对(a,b)叫做点A的坐标
x
在平面直角坐标系中的点和有序实数对是一一对应的.
(0,0)
A
·
B
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
·
C
·
A
·
E
·
D
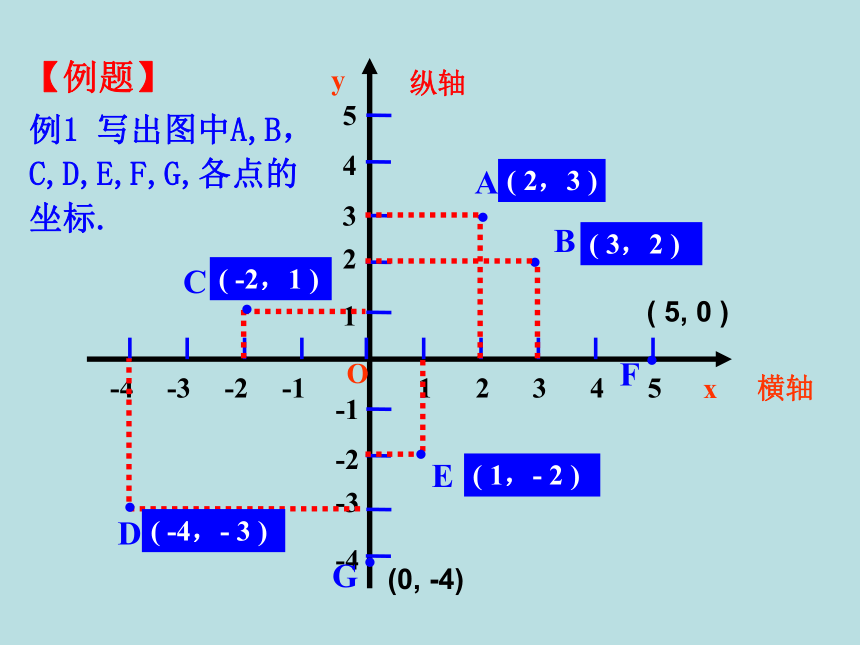
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
例1 写出图中A,B,C,D,E,F,G,各点的坐标.
纵轴
【例题】
F·
( 5, 0 )
G·
(0, -4)
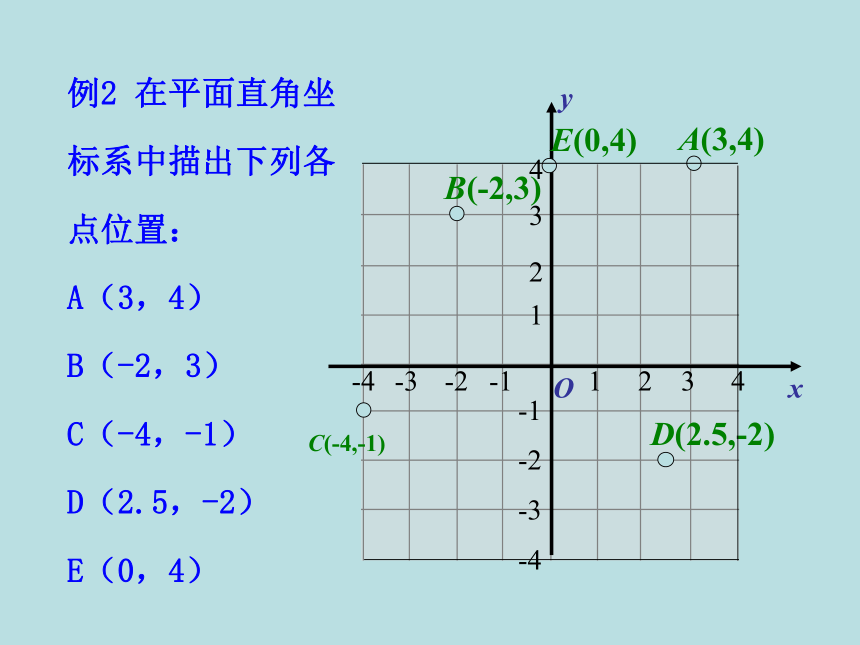
例2 在平面直角坐标系中描出下列各点位置:
A(3,4)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,4)
-3
-2
-1
1
2
3
-4
4
x
-1
-2
-3
-4
1
2
3
4
y
O
A(3,4)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,4)
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
O
-3
x
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
归纳总结:
1.在四个象限内的点的坐标各有什么特征?
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
( - , - )
(+, - )
y
4
2
5
3
6
·
C
(0,-3)
1
2
3
-3
x
-2
·
-2
-3
o
-1
1
·
·
·
-4
-1
4
·
B
(0,3)
D
E
(-2,0)
(2,0)
x轴上的点的纵坐标为0,表示为(x, 0)
y轴上的点的横坐标为0,表示为(0, y)
(0,6)
A
2.两条坐标轴上的点的坐标各有什么特征?
3、如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A.第四象限 B.第三象限
C.第二象限 D.第一象限
D
1、已知点P( -3 , 2 ),则点P在_______象限.
2、已知点Q(0,-3),则点Q的位置在_______.
第二
y轴上
【跟踪训练】
4、直角坐标系中有一点 M(a,b),其中ab=0 ,则点M的位置在( )
A.原点 B.x轴上 C.y轴上 D.坐标轴上
D
5、矩形ABCD中, A,B,C三点的坐标分别是(0,0), (5,0),(5,3), D点的坐标是( ).
A.(0,5) B.(5,0) C.(0,3) D.(3,0)
C
探索发现:
在平面直角坐标系中描出点A(3,2),分别找出它关于x轴,y轴及原点的对称点,并写出这些点的坐标.
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
O
-3
x
1.关于x轴对称的两点,横坐标相等,纵坐标互为相反数;
2.关于y轴对称的两点,横坐标互为相反数,纵坐标相等;
3.关于原点对称的两点,横坐标、纵坐标分别互为相反数.
1.点A(2,-3)关于x轴对称的点坐标为_______.
关于y轴对称的点坐标为_________.
关于原点对称的点坐标为________.
(2,3)
(-2,-3)
(-2,3)
2.点(3,5)与点(3,-5)关于______轴对称.
x
3.点A关于原点对称点的坐标为(2,3),则点A关于
y 轴对称点的坐标为 .
(2,-3)
【跟踪训练】
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 .
四
三
y
-1
(4, 0 )或(-4, 0 )
课堂检测
O
(1)点(2,3)到x轴的距离为 ,
到y轴的距离为 .
(2)点(-2,-3)到x轴的距离为 ,
到y轴的距离为 .
(3)点(a,b)到x轴的距离为 ,
到y轴的距离为 .
3
2
3
2
b
a
3.填空
4. 如图, 矩形ABCD的长宽分别是6、4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解: 如图,以点C
为坐标原点, 分别
以CD、CB所在的
直线为x 轴、y 轴
建立直角坐标系.
此时C点坐标为(0,0).
由CD长为6, CB长
为4,可得D、B、A的
坐标分别为D(6,0)、 B(0,4)、A(6, 4) .
x
y
O
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
1
1
4. 如图, 矩形ABCD的长宽分别是6、4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
x
y
O
1.能画出平面直角坐标系,理解坐标平面内点的横坐标和纵坐标的意义,并会在坐标系内由点求坐标,由坐标找点;
2.通过归纳,得出坐标系中各个象限及坐标轴上的点的特征;
3.掌握关于X轴、Y轴、坐标原点对称点的坐标特征;
4.体会坐标平面内的点与有序实数对的一一对应关系,体会其中数形结合的意义.
1.教材第35页练习第1、2、3题.
2.教材第41页习题17.2第1、2、3题.
谢谢同学们!
17.2 函数的图象
1 平面直角坐标系
华师大版八年级数学(下)
概念: 在平面内,画两条原点重合、互相垂直且具有相同单位长度的数轴组成平面直角坐标系
y轴(纵轴)
x轴(横轴)
坐标原点
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
·
M
N ·
(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度相同
说一说:平面直角坐标系中两条数轴具有哪些特征呢?
-4 -3 -2 -1 1 2 3 4
O
x
y
4
3
2
1
-1
-2
-3
-4
·
A
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x轴上的坐标为4
A点在y轴上的坐标为2
A点在平面直角坐标系中的
坐标为(4, 2)记作:A(4,2)
x轴上的坐标
写在前面
·
B
(-4, 1)
o
y
(a,b)
b
a
对于平面内任意一点A,
过点A分别作x轴,y轴的
垂线,垂足在x轴,y轴上对应的数a,b分别叫做点A
的横坐标、纵坐标,有序
实数对(a,b)叫做点A的坐标
x
在平面直角坐标系中的点和有序实数对是一一对应的.
(0,0)
A
·
B
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
例1 写出图中A,B,C,D,E,F,G,各点的坐标.
纵轴
【例题】
F·
( 5, 0 )
G·
(0, -4)
例2 在平面直角坐标系中描出下列各点位置:
A(3,4)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,4)
-3
-2
-1
1
2
3
-4
4
x
-1
-2
-3
-4
1
2
3
4
y
O
A(3,4)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,4)
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
O
-3
x
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
归纳总结:
1.在四个象限内的点的坐标各有什么特征?
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
( - , - )
(+, - )
y
4
2
5
3
6
·
C
(0,-3)
1
2
3
-3
x
-2
·
-2
-3
o
-1
1
·
·
·
-4
-1
4
·
B
(0,3)
D
E
(-2,0)
(2,0)
x轴上的点的纵坐标为0,表示为(x, 0)
y轴上的点的横坐标为0,表示为(0, y)
(0,6)
A
2.两条坐标轴上的点的坐标各有什么特征?
3、如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A.第四象限 B.第三象限
C.第二象限 D.第一象限
D
1、已知点P( -3 , 2 ),则点P在_______象限.
2、已知点Q(0,-3),则点Q的位置在_______.
第二
y轴上
【跟踪训练】
4、直角坐标系中有一点 M(a,b),其中ab=0 ,则点M的位置在( )
A.原点 B.x轴上 C.y轴上 D.坐标轴上
D
5、矩形ABCD中, A,B,C三点的坐标分别是(0,0), (5,0),(5,3), D点的坐标是( ).
A.(0,5) B.(5,0) C.(0,3) D.(3,0)
C
探索发现:
在平面直角坐标系中描出点A(3,2),分别找出它关于x轴,y轴及原点的对称点,并写出这些点的坐标.
A(3,2)
B(3,-2)
C(-3,2)
D(-3,-2)
·
·
·
·
y
1
2
3
4
5
-2
-1
-4
3
1
4
2
5
-2
-4
-1
-3
O
-3
x
1.关于x轴对称的两点,横坐标相等,纵坐标互为相反数;
2.关于y轴对称的两点,横坐标互为相反数,纵坐标相等;
3.关于原点对称的两点,横坐标、纵坐标分别互为相反数.
1.点A(2,-3)关于x轴对称的点坐标为_______.
关于y轴对称的点坐标为_________.
关于原点对称的点坐标为________.
(2,3)
(-2,-3)
(-2,3)
2.点(3,5)与点(3,-5)关于______轴对称.
x
3.点A关于原点对称点的坐标为(2,3),则点A关于
y 轴对称点的坐标为 .
(2,-3)
【跟踪训练】
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 .
四
三
y
-1
(4, 0 )或(-4, 0 )
课堂检测
O
(1)点(2,3)到x轴的距离为 ,
到y轴的距离为 .
(2)点(-2,-3)到x轴的距离为 ,
到y轴的距离为 .
(3)点(a,b)到x轴的距离为 ,
到y轴的距离为 .
3
2
3
2
b
a
3.填空
4. 如图, 矩形ABCD的长宽分别是6、4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解: 如图,以点C
为坐标原点, 分别
以CD、CB所在的
直线为x 轴、y 轴
建立直角坐标系.
此时C点坐标为(0,0).
由CD长为6, CB长
为4,可得D、B、A的
坐标分别为D(6,0)、 B(0,4)、A(6, 4) .
x
y
O
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
1
1
4. 如图, 矩形ABCD的长宽分别是6、4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
x
y
O
1.能画出平面直角坐标系,理解坐标平面内点的横坐标和纵坐标的意义,并会在坐标系内由点求坐标,由坐标找点;
2.通过归纳,得出坐标系中各个象限及坐标轴上的点的特征;
3.掌握关于X轴、Y轴、坐标原点对称点的坐标特征;
4.体会坐标平面内的点与有序实数对的一一对应关系,体会其中数形结合的意义.
1.教材第35页练习第1、2、3题.
2.教材第41页习题17.2第1、2、3题.
谢谢同学们!
