冀教版七年级数学下册11.3.1 公式法 课件 (共23张PPT)
文档属性
| 名称 | 冀教版七年级数学下册11.3.1 公式法 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 859.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:14:00 | ||
图片预览






文档简介
(共23张PPT)
11.3.1公式法
能说出平方差公式的结构特征.
能较熟练地应用平方差公式分解因式.
经历用乘法公式探索分解因式方法的过程,体会从正反两方面认识和研究事物的方法.
学习目标
1
2
3
掌握用平方差公式分解因式的方法.
能综合运用提取公因式法、平方差公式法分解因式.
学习重难点
重点:
难点:
情景导入
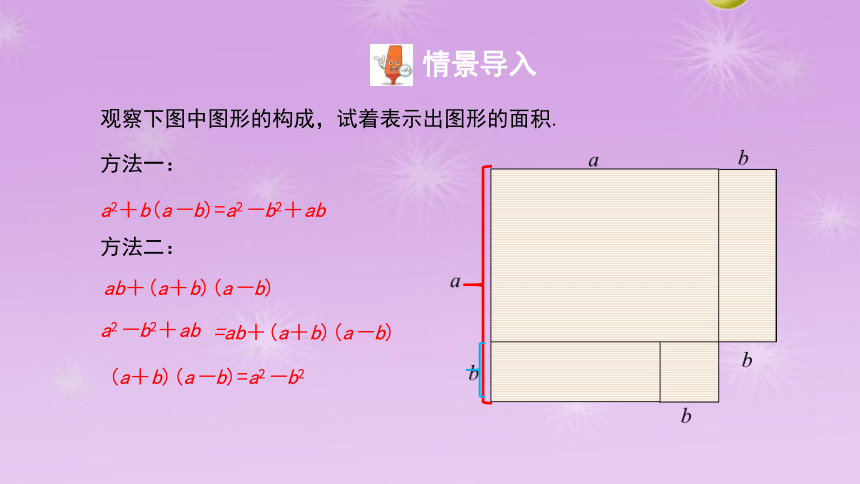
观察下图中图形的构成,试着表示出图形的面积.
a2+b(a-b)=a2-b2+ab
ab+(a+b)(a-b)
方法一:
方法二:
a2-b2+ab
=ab+(a+b)(a-b)
(a+b)(a-b)=a2-b2
事实上,把乘法公式(平方差公式) =(a+b)(a-b)= a -b ,
反过来,就得到因式分解的(平方差公式):a -b =(a+b)(a-b)
探究新知
填空:
(1)(x+5)(x-5)= ;
(2)(3x+y)(3x-y)= ;
(3)(3m+2n)(3m-2n)= .
尝试将它们的结果分别写成两个因式的乘积:
(1)x2-25= ;
(2)9x2-y2= ;
(3)9m2-4n2= .
x2-25
9x2-y2
9m2-4n2
(x+5)(x-5)
(3x+y)(3x-y)
(3m+2n)(3m-2n)
探究新知
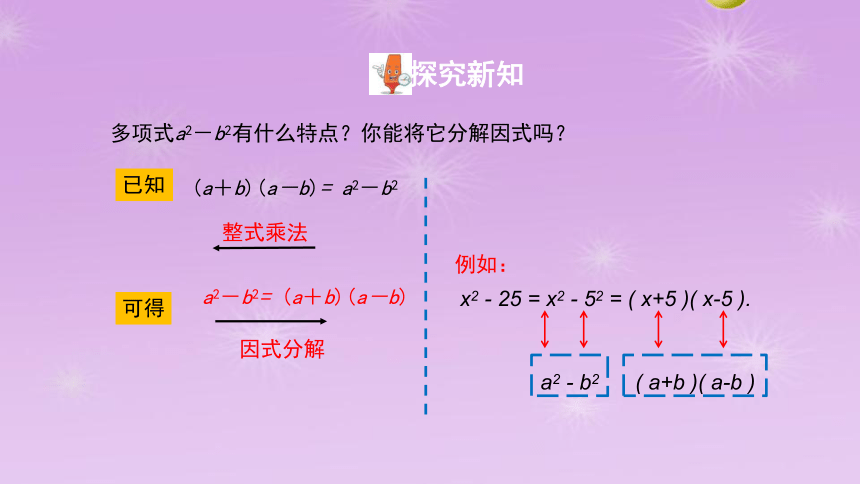
多项式a2-b2有什么特点?你能将它分解因式吗?
已知
(a+b)(a-b)= a2-b2
可得
a2-b2= (a+b)(a-b)
因式分解
整式乘法
x2 - 25 = x2 - 52 = ( x+5 )( x-5 ).
a2 - b2
( a+b )( a-b )
例如:
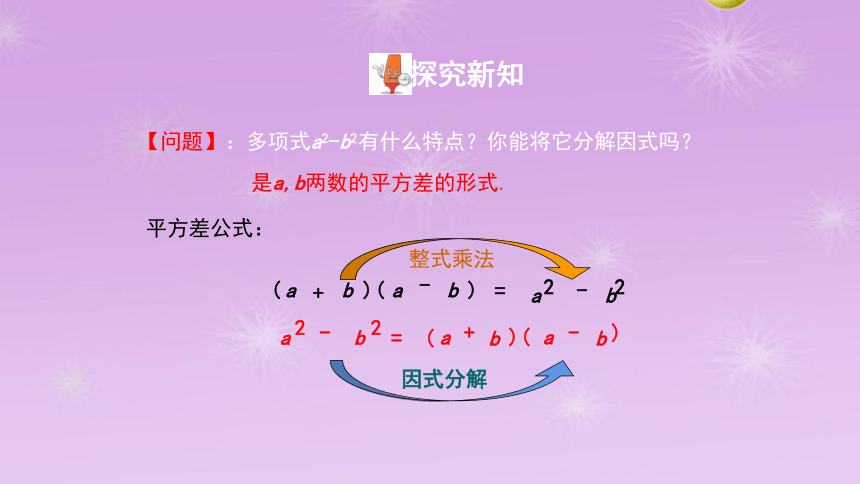
【问题】:多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式.
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
平方差公式:
探究新知
归纳
如果一个二项式,它能够化成两个整式的平方差,就可以用平方差公式分解因式,分解成两个整式的和与差的积.
典例精析
【例1】把下列各式分解因式.
解:4x2-9y2
=(2x) -(3y) 2
=(2x+3y) (2x-3y) .
(1)4x2-9y2;
(2)(3m-1)2-9.
解:(3m-1) -9
=(3m-1) -32
=(3m-1+3)(3m-1-3)
=(3m+2)(3m-4) .
即学即练
分解因式:x4-y4
解:x4-y4
= (x2+y2)(x2-y2)
= (x2+y2)(x+y)(x-y).
方法归纳:分解因式,必须进行到每一个多项式都不能再分解为止.
归纳
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
因式分解—平方差公式的逆用
判断能否用平方差公式应过几关?
三关:
(1)项数关:
(2)符号关:
(3)平方关:
2项
相反
每一项的绝对值都可化为某个整式的平方.
观察公式有何特征?
合作探究
即学即练
下列各式能用平方差公式因式分解吗?为什么?
A.m +n B.-m -n C.-m +n D. m -tn
解:A.m +n 的两平方项符号相同,不能用平方差公式进行因式分解;
B.-m -n 的两平方项符号相同,不能用平方差公式进行因式分解;
C.-m +n 符合平方差公式的特点,能用平方差公式进行因式分解;
D. m -tn 不符合平方差公式的特点,不能用平方差公式进行因式分解.
问题:
【例2】把下列各式分解因式.
(2)2ab3-2ab
=2ab(b2-1)
=2ab(b+1)(b-1).
典例精析
(1)a3-16a;
(2)2ab3-2ab.
解:(1) a3-16a
=a(a2-16)
=a(a-4)(a+4) .
当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步因式分解.
即学即练
把x3-9x分解因式,结果正确的是( )
A.x(x2-9) B.x(x-3)2
C.x(x+3)2 D.x(x+3)(x-3)
D
归纳:因式分解,必须进行到每一个多项式因式都不能再分解为止.
课堂练习
1. 将下列多项式分解因式:
① a2- 25 = ___________________
② 9a2-b2= ___________________
③ (a+b)2-9a2 = ________________
④ -a4+16 = ___________________
(a+5)(a–5)
(3a+b)(3a-b)
(4a+b)(b-2a)
(4+a2)(2+a)(2-a)
课堂练习
2. 因式分解的结果是(x+y﹣z)(x﹣y+z)的多项式是( )
A.x2﹣(y+z)2 B.(x﹣y)2﹣z 2
C.﹣(x﹣y)2+z2 D.x2﹣(y﹣z)2
A
3.因式分解x2-4y2的结果是( )
A.(x+4y)(x-4y) B.(x+2y)(x-2y)
C.(x-4y)2 D.(x-2y)2
B
4.(1)9y2=( )2; (2) =( )2;
3y
5.把下列多项式因式分解:
(1)9y2-4x2; (2)( x+y )2-( y-x )2;
(3)x4-16; (4)a3-ab2.
答案:(1)( 3y+2x )( 3y-2x );(2)4xy;(3)( x2+4 )( x+2 )( x-2 );(4)a( a+b )( a-b ).
课堂练习
6.把( x+y )2 - ( x-y )2因式分解.
解:( x+y )2 - ( x-y )2
= [( x+y )+( x-y )][( x+y ) - ( x-y )]
= 2x·2y
= 4xy.
课堂练习
6.把x3y2 - x5因式分解.
解:x3y2 - x5
=x3( y2 - x2 )
=x3( y + x )( y - x ).
7.把x4-y4因式分解.
在因式分解时,必须进行到每一个因式都不能分解为止.
8.把25x2-4y2因式分解.
解:25x2-4y2
=( 5x )2 - ( 2y )2
=( 5x+2y )( 5x-2y ).
解
:
x4-y4
=
(
x2
)
2
-
(
y2
)
2
=
(
x2
+
y2
)(
x2
-
y2
)
=
(
x2
+
y2
)
(
x
+
y
)
(
x
-
y
).
课堂练习
课堂练习
9. 已知:a2-b2=21, a-b=3,求代数式(a-3b)2的值.
解: 因为 a-b=3,
所以(a+b)(a-b)=21,
所以 a+b=7
由 a-b=3和a+b=7解得
a=5,b=2
所以(a-3b)2
=(5-3×2)2 =1.
总结
用平方差公式因式分解
依据
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
a2-b2=(a+b)(a-b)
与提公因式法综合运用
①提取公因式;
②运用平方差公式;
③检查多项式的因式分解是否完全,有没有分解到不能再分解为止.
谢谢听讲!
11.3.1公式法
能说出平方差公式的结构特征.
能较熟练地应用平方差公式分解因式.
经历用乘法公式探索分解因式方法的过程,体会从正反两方面认识和研究事物的方法.
学习目标
1
2
3
掌握用平方差公式分解因式的方法.
能综合运用提取公因式法、平方差公式法分解因式.
学习重难点
重点:
难点:
情景导入
观察下图中图形的构成,试着表示出图形的面积.
a2+b(a-b)=a2-b2+ab
ab+(a+b)(a-b)
方法一:
方法二:
a2-b2+ab
=ab+(a+b)(a-b)
(a+b)(a-b)=a2-b2
事实上,把乘法公式(平方差公式) =(a+b)(a-b)= a -b ,
反过来,就得到因式分解的(平方差公式):a -b =(a+b)(a-b)
探究新知
填空:
(1)(x+5)(x-5)= ;
(2)(3x+y)(3x-y)= ;
(3)(3m+2n)(3m-2n)= .
尝试将它们的结果分别写成两个因式的乘积:
(1)x2-25= ;
(2)9x2-y2= ;
(3)9m2-4n2= .
x2-25
9x2-y2
9m2-4n2
(x+5)(x-5)
(3x+y)(3x-y)
(3m+2n)(3m-2n)
探究新知
多项式a2-b2有什么特点?你能将它分解因式吗?
已知
(a+b)(a-b)= a2-b2
可得
a2-b2= (a+b)(a-b)
因式分解
整式乘法
x2 - 25 = x2 - 52 = ( x+5 )( x-5 ).
a2 - b2
( a+b )( a-b )
例如:
【问题】:多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式.
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
平方差公式:
探究新知
归纳
如果一个二项式,它能够化成两个整式的平方差,就可以用平方差公式分解因式,分解成两个整式的和与差的积.
典例精析
【例1】把下列各式分解因式.
解:4x2-9y2
=(2x) -(3y) 2
=(2x+3y) (2x-3y) .
(1)4x2-9y2;
(2)(3m-1)2-9.
解:(3m-1) -9
=(3m-1) -32
=(3m-1+3)(3m-1-3)
=(3m+2)(3m-4) .
即学即练
分解因式:x4-y4
解:x4-y4
= (x2+y2)(x2-y2)
= (x2+y2)(x+y)(x-y).
方法归纳:分解因式,必须进行到每一个多项式都不能再分解为止.
归纳
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
因式分解—平方差公式的逆用
判断能否用平方差公式应过几关?
三关:
(1)项数关:
(2)符号关:
(3)平方关:
2项
相反
每一项的绝对值都可化为某个整式的平方.
观察公式有何特征?
合作探究
即学即练
下列各式能用平方差公式因式分解吗?为什么?
A.m +n B.-m -n C.-m +n D. m -tn
解:A.m +n 的两平方项符号相同,不能用平方差公式进行因式分解;
B.-m -n 的两平方项符号相同,不能用平方差公式进行因式分解;
C.-m +n 符合平方差公式的特点,能用平方差公式进行因式分解;
D. m -tn 不符合平方差公式的特点,不能用平方差公式进行因式分解.
问题:
【例2】把下列各式分解因式.
(2)2ab3-2ab
=2ab(b2-1)
=2ab(b+1)(b-1).
典例精析
(1)a3-16a;
(2)2ab3-2ab.
解:(1) a3-16a
=a(a2-16)
=a(a-4)(a+4) .
当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步因式分解.
即学即练
把x3-9x分解因式,结果正确的是( )
A.x(x2-9) B.x(x-3)2
C.x(x+3)2 D.x(x+3)(x-3)
D
归纳:因式分解,必须进行到每一个多项式因式都不能再分解为止.
课堂练习
1. 将下列多项式分解因式:
① a2- 25 = ___________________
② 9a2-b2= ___________________
③ (a+b)2-9a2 = ________________
④ -a4+16 = ___________________
(a+5)(a–5)
(3a+b)(3a-b)
(4a+b)(b-2a)
(4+a2)(2+a)(2-a)
课堂练习
2. 因式分解的结果是(x+y﹣z)(x﹣y+z)的多项式是( )
A.x2﹣(y+z)2 B.(x﹣y)2﹣z 2
C.﹣(x﹣y)2+z2 D.x2﹣(y﹣z)2
A
3.因式分解x2-4y2的结果是( )
A.(x+4y)(x-4y) B.(x+2y)(x-2y)
C.(x-4y)2 D.(x-2y)2
B
4.(1)9y2=( )2; (2) =( )2;
3y
5.把下列多项式因式分解:
(1)9y2-4x2; (2)( x+y )2-( y-x )2;
(3)x4-16; (4)a3-ab2.
答案:(1)( 3y+2x )( 3y-2x );(2)4xy;(3)( x2+4 )( x+2 )( x-2 );(4)a( a+b )( a-b ).
课堂练习
6.把( x+y )2 - ( x-y )2因式分解.
解:( x+y )2 - ( x-y )2
= [( x+y )+( x-y )][( x+y ) - ( x-y )]
= 2x·2y
= 4xy.
课堂练习
6.把x3y2 - x5因式分解.
解:x3y2 - x5
=x3( y2 - x2 )
=x3( y + x )( y - x ).
7.把x4-y4因式分解.
在因式分解时,必须进行到每一个因式都不能分解为止.
8.把25x2-4y2因式分解.
解:25x2-4y2
=( 5x )2 - ( 2y )2
=( 5x+2y )( 5x-2y ).
解
:
x4-y4
=
(
x2
)
2
-
(
y2
)
2
=
(
x2
+
y2
)(
x2
-
y2
)
=
(
x2
+
y2
)
(
x
+
y
)
(
x
-
y
).
课堂练习
课堂练习
9. 已知:a2-b2=21, a-b=3,求代数式(a-3b)2的值.
解: 因为 a-b=3,
所以(a+b)(a-b)=21,
所以 a+b=7
由 a-b=3和a+b=7解得
a=5,b=2
所以(a-3b)2
=(5-3×2)2 =1.
总结
用平方差公式因式分解
依据
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
a2-b2=(a+b)(a-b)
与提公因式法综合运用
①提取公因式;
②运用平方差公式;
③检查多项式的因式分解是否完全,有没有分解到不能再分解为止.
谢谢听讲!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
