冀教版七年级数学下册6.3二元一次方程组的应用 课件 (共26张PPT)
文档属性
| 名称 | 冀教版七年级数学下册6.3二元一次方程组的应用 课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 877.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
实际问题与二元一次方程组
学习目标
1、能够分析题意,根据具体的数量关系,列出二元一次方程组并解决实际问题。
2、经历用方程组解决实际图形问题的过程,体会方程组是刻画现实世界的有效数学模型。
重点
难点
重难点
学会利用二元一次方程组解决实际问题。
能够根据具体的数量关系,列出二元一次方程组。
例1
解:设平均每只大牛和每只小牛1天各约用饲料xkg和ykg.
养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940 kg.饲养员李大叔估计平均每只大牛1天约需要饲料18~20 kg,每只小牛1天约需要7~8 kg.你能否通过计算检验他的估计?
(1)30只大牛1天所需饲料+15只小牛1天所需饲料=1天的饲料总量;
(2)42只大牛1天所需饲料+20只小牛1天所需饲料=后来1天的饲料总量.
30x+15y=675
42x+20y=940
解方程组,得:
20
5
因此,饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
答:平均每只大牛和每只小牛1天各约用饲料20kg和5kg。
例1
练习
有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨, 3辆大车与5辆小车一次可以运货多少吨?
解:设一辆大车一次可以运货x吨,一辆小车一次可以运货y吨.
解这个方程组,得
答:3辆大车和5辆小车一次可以运24.5吨。
所以3辆大车和5辆小车为 3x+5y=3×4+5×2.5=24.5
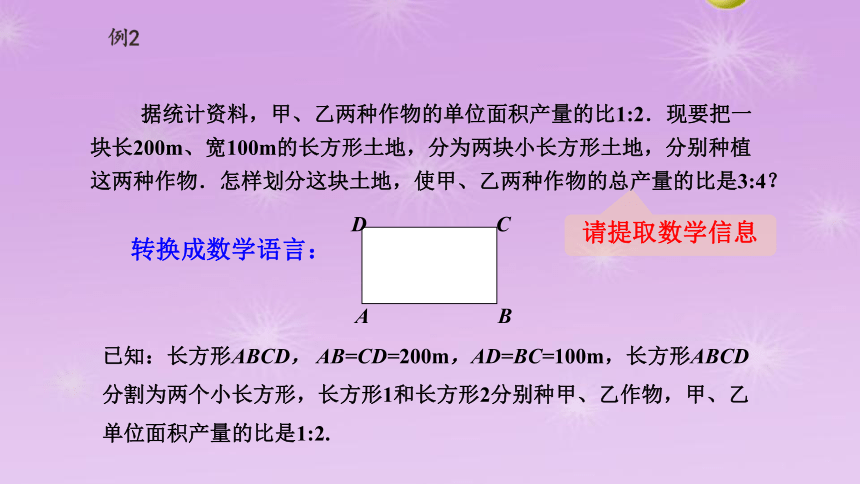
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
例2
竖着画,把长分成两段,则宽不变
2.甲、乙两种作物总产量比=3:4
SAEFD=100x
SEFCB=100y
甲:100x×1
乙:100y×2
100x:200y=3:4
如何设未知数呢?
1.设AE=x m,BE=y m
则列方程为 x+y=200
总产量=单位面积产量×面积
A
D
C
F
B
E
1 : 2
x
y
200
100
例2
横着画,把宽分成两段,则长不变
解:过点E 作EF⊥BC,交BC于点F. 设DE=x m,AE=y m
根据题意列方程组为
答:将这块土地分为长200m,宽60m和长200m,宽40m的两个小长方形分别种植甲、乙两种作物.
A
D
C
B
E
x
y
F
乙种作物
甲种作物
200y
200x
100m
200
100
例2
练习
某车间28名工人参加生产某种特制的螺丝和螺母.已知平均每人每天能生产螺丝12个或螺母18个,1个螺丝装配2个螺母.怎样安排生产螺丝和螺母的工人,才能使每天的产品配套
解:设每天安排x人生产螺丝,y人生产螺母,那么每天能生产螺丝12x个,螺母18y个。
答:应安排12人生产螺丝,16人生产螺母。
根据题意得
例3
如图,长青化工厂与A,B 两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
产品x 吨 原料y 吨 合计
公路运费(元) 1.5×20x 1.5×10y
铁路运费(元) 1.2×110x 1.2×120y
价值(元) 8 000x 1 000y
根据题意,完成表格:
1.5(20x+10y)
1.2(110x+120y)
例3
答这批产品的销售款比原料费与运输费的和多1887800元.
所以产品300吨,原料400吨;
总销售额=300×8000=2400000元;
原材料+运输费=400×1000+15000+97200=512200元;
总销售额-(原材料+运输费)=1887800元;
例3
练习
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5
5x+ 6y=35
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735(元).
答:货主应付运费735元.
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
练习
基础巩固
某单位组织34人分别到井冈山和瑞金进行革命传统教育,到井冈山的人数是到瑞金人数的2倍多1人,求到两地的人数各是多少.设到井冈山的人数为x人,到瑞金的人数为y人,请列出满足题意的方程组: .
学校举行“大家唱,大家跳”文艺会演,设置了歌唱与舞蹈两类节目,全校师生一共表演了30个节目,其中歌唱类节目比舞蹈类节目的3倍少2个,则全校师生表演的歌唱类节目有 个.
22
基础巩固
25名工人按定额完成了2200件产品,其中三级工每人每天定额200件,二级工每人每天定额60件.若这25名工人只有二级工与三级工,问二级工与三级工各有多少名?
解:设二级工有x名,三级工有y名.根据题意,有
答:二级工有20名,三级工有5名。
基础巩固
小刚骑摩托车在公路上高速匀速行驶,8:00时看到里程碑上的数是一个两位数,它的数字之和是7;9:00时看里程碑上的两位数与8:00时看到的个位数和十位数颠倒了;10:00时看到里程碑上的数比8:00时看到的两位数中间多了个零,小刚在8:00时看到里程碑上的数字是多少?
解:设小刚在8:00时看到的数字的十位数字是x,个位的数字是y,那么
答:小刚在8:00时看到的数字是16
基础巩固
第一个数的8%与第二个数的9%的和是67,第一个数的9%与第二个数的8%的差是19.求这两个数.
答:第一个数为500,第二个数为300.
解:设第一个数为x,第二个数为y,依题意,得
基础巩固
欲将某河上游A地的一部分牧场改为林场.改变后,林场和牧场共有160公顷, 林场面积是牧场面积的7倍, 试问完成后林场、牧场的面积各为多少公顷?
解:设完成后林场面积为x公顷,牧场面积为y公顷,
根据题意,有
答:完成后林场面积为140公顷,牧场面积为20公顷。
基础巩固
某车间每天能生产甲种零件600个或乙种零件300个,或丙种零件500个,甲、乙、丙三种零件各1个就可以配成一套,要在63天内的生产中,使生产的零件全部成套,问甲、乙、丙三种零件各应生产几天?
答:甲、乙、丙三种零件各应生产15天、30天和18天.
基础巩固
解:设甲零件生产x天,乙零件生产y天,则丙零件生产(63-x-y)天,根据题意,得
所以63-x-y=18.
步骤
二元一次方程组是解决两个未知数问题的有效模型.运用二元一次方程组解决实际问题的步骤:
(1)弄清题意和题目中的数量关系,用字母(如x,y)表示题目中的两个未知数;
(2)找出能够表示应用题全部含义的两个相等关系;
(3)根据这两个相等关系列出需要的代数式,从而列出方程并组成方程组;
(4)解这个方程组,求出未知数的值;
(5)根据应用题的实际意义,检查求得的结果是否合理,然后写出答案.
步骤
弄清题意,找出题目中的等量关系
设未知数,根据等量关系列出方程组
解方程组并检验
根据所得解,写出问题所求
课堂总结
列方程组解决实际问题
解决实际问题的基本步骤
知识
考点
解决配套问题、方案设计问题
解决路程问题、工程问题
解决数字问题、和差倍分问题等
实际问题与二元一次方程组
学习目标
1、能够分析题意,根据具体的数量关系,列出二元一次方程组并解决实际问题。
2、经历用方程组解决实际图形问题的过程,体会方程组是刻画现实世界的有效数学模型。
重点
难点
重难点
学会利用二元一次方程组解决实际问题。
能够根据具体的数量关系,列出二元一次方程组。
例1
解:设平均每只大牛和每只小牛1天各约用饲料xkg和ykg.
养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940 kg.饲养员李大叔估计平均每只大牛1天约需要饲料18~20 kg,每只小牛1天约需要7~8 kg.你能否通过计算检验他的估计?
(1)30只大牛1天所需饲料+15只小牛1天所需饲料=1天的饲料总量;
(2)42只大牛1天所需饲料+20只小牛1天所需饲料=后来1天的饲料总量.
30x+15y=675
42x+20y=940
解方程组,得:
20
5
因此,饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
答:平均每只大牛和每只小牛1天各约用饲料20kg和5kg。
例1
练习
有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨, 3辆大车与5辆小车一次可以运货多少吨?
解:设一辆大车一次可以运货x吨,一辆小车一次可以运货y吨.
解这个方程组,得
答:3辆大车和5辆小车一次可以运24.5吨。
所以3辆大车和5辆小车为 3x+5y=3×4+5×2.5=24.5
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
例2
竖着画,把长分成两段,则宽不变
2.甲、乙两种作物总产量比=3:4
SAEFD=100x
SEFCB=100y
甲:100x×1
乙:100y×2
100x:200y=3:4
如何设未知数呢?
1.设AE=x m,BE=y m
则列方程为 x+y=200
总产量=单位面积产量×面积
A
D
C
F
B
E
1 : 2
x
y
200
100
例2
横着画,把宽分成两段,则长不变
解:过点E 作EF⊥BC,交BC于点F. 设DE=x m,AE=y m
根据题意列方程组为
答:将这块土地分为长200m,宽60m和长200m,宽40m的两个小长方形分别种植甲、乙两种作物.
A
D
C
B
E
x
y
F
乙种作物
甲种作物
200y
200x
100m
200
100
例2
练习
某车间28名工人参加生产某种特制的螺丝和螺母.已知平均每人每天能生产螺丝12个或螺母18个,1个螺丝装配2个螺母.怎样安排生产螺丝和螺母的工人,才能使每天的产品配套
解:设每天安排x人生产螺丝,y人生产螺母,那么每天能生产螺丝12x个,螺母18y个。
答:应安排12人生产螺丝,16人生产螺母。
根据题意得
例3
如图,长青化工厂与A,B 两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
产品x 吨 原料y 吨 合计
公路运费(元) 1.5×20x 1.5×10y
铁路运费(元) 1.2×110x 1.2×120y
价值(元) 8 000x 1 000y
根据题意,完成表格:
1.5(20x+10y)
1.2(110x+120y)
例3
答这批产品的销售款比原料费与运输费的和多1887800元.
所以产品300吨,原料400吨;
总销售额=300×8000=2400000元;
原材料+运输费=400×1000+15000+97200=512200元;
总销售额-(原材料+运输费)=1887800元;
例3
练习
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5
5x+ 6y=35
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735(元).
答:货主应付运费735元.
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
练习
基础巩固
某单位组织34人分别到井冈山和瑞金进行革命传统教育,到井冈山的人数是到瑞金人数的2倍多1人,求到两地的人数各是多少.设到井冈山的人数为x人,到瑞金的人数为y人,请列出满足题意的方程组: .
学校举行“大家唱,大家跳”文艺会演,设置了歌唱与舞蹈两类节目,全校师生一共表演了30个节目,其中歌唱类节目比舞蹈类节目的3倍少2个,则全校师生表演的歌唱类节目有 个.
22
基础巩固
25名工人按定额完成了2200件产品,其中三级工每人每天定额200件,二级工每人每天定额60件.若这25名工人只有二级工与三级工,问二级工与三级工各有多少名?
解:设二级工有x名,三级工有y名.根据题意,有
答:二级工有20名,三级工有5名。
基础巩固
小刚骑摩托车在公路上高速匀速行驶,8:00时看到里程碑上的数是一个两位数,它的数字之和是7;9:00时看里程碑上的两位数与8:00时看到的个位数和十位数颠倒了;10:00时看到里程碑上的数比8:00时看到的两位数中间多了个零,小刚在8:00时看到里程碑上的数字是多少?
解:设小刚在8:00时看到的数字的十位数字是x,个位的数字是y,那么
答:小刚在8:00时看到的数字是16
基础巩固
第一个数的8%与第二个数的9%的和是67,第一个数的9%与第二个数的8%的差是19.求这两个数.
答:第一个数为500,第二个数为300.
解:设第一个数为x,第二个数为y,依题意,得
基础巩固
欲将某河上游A地的一部分牧场改为林场.改变后,林场和牧场共有160公顷, 林场面积是牧场面积的7倍, 试问完成后林场、牧场的面积各为多少公顷?
解:设完成后林场面积为x公顷,牧场面积为y公顷,
根据题意,有
答:完成后林场面积为140公顷,牧场面积为20公顷。
基础巩固
某车间每天能生产甲种零件600个或乙种零件300个,或丙种零件500个,甲、乙、丙三种零件各1个就可以配成一套,要在63天内的生产中,使生产的零件全部成套,问甲、乙、丙三种零件各应生产几天?
答:甲、乙、丙三种零件各应生产15天、30天和18天.
基础巩固
解:设甲零件生产x天,乙零件生产y天,则丙零件生产(63-x-y)天,根据题意,得
所以63-x-y=18.
步骤
二元一次方程组是解决两个未知数问题的有效模型.运用二元一次方程组解决实际问题的步骤:
(1)弄清题意和题目中的数量关系,用字母(如x,y)表示题目中的两个未知数;
(2)找出能够表示应用题全部含义的两个相等关系;
(3)根据这两个相等关系列出需要的代数式,从而列出方程并组成方程组;
(4)解这个方程组,求出未知数的值;
(5)根据应用题的实际意义,检查求得的结果是否合理,然后写出答案.
步骤
弄清题意,找出题目中的等量关系
设未知数,根据等量关系列出方程组
解方程组并检验
根据所得解,写出问题所求
课堂总结
列方程组解决实际问题
解决实际问题的基本步骤
知识
考点
解决配套问题、方案设计问题
解决路程问题、工程问题
解决数字问题、和差倍分问题等
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
