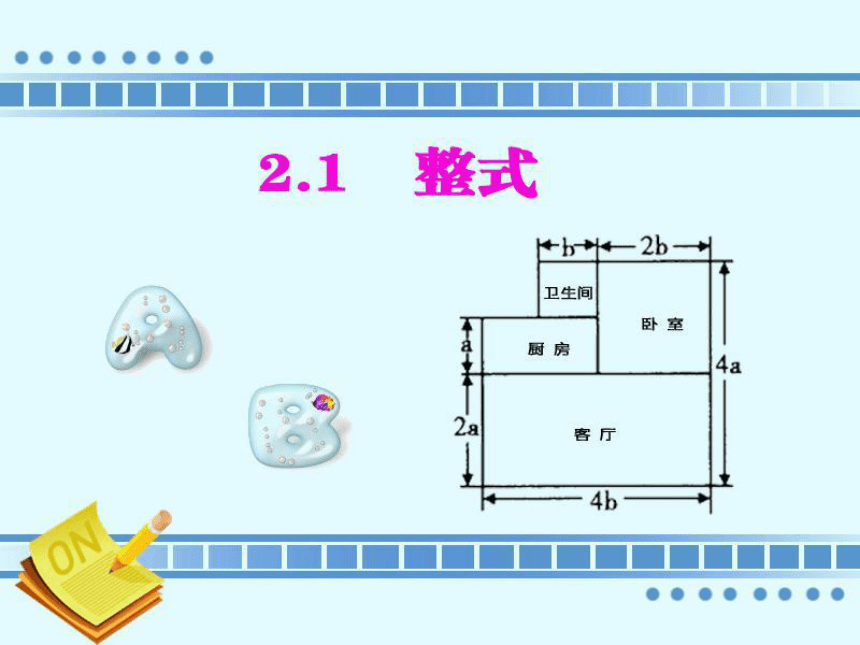
2.1整式
图片预览







文档简介
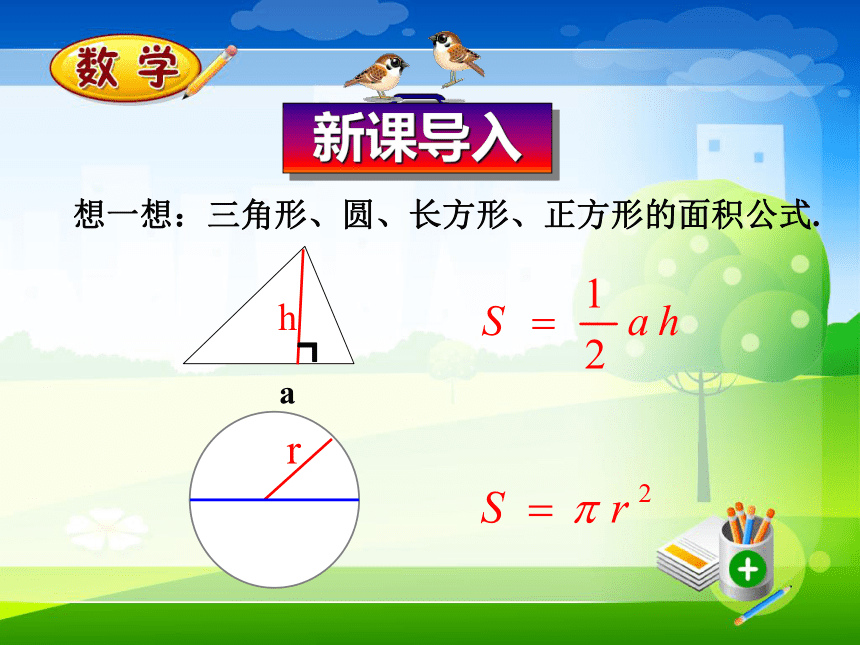
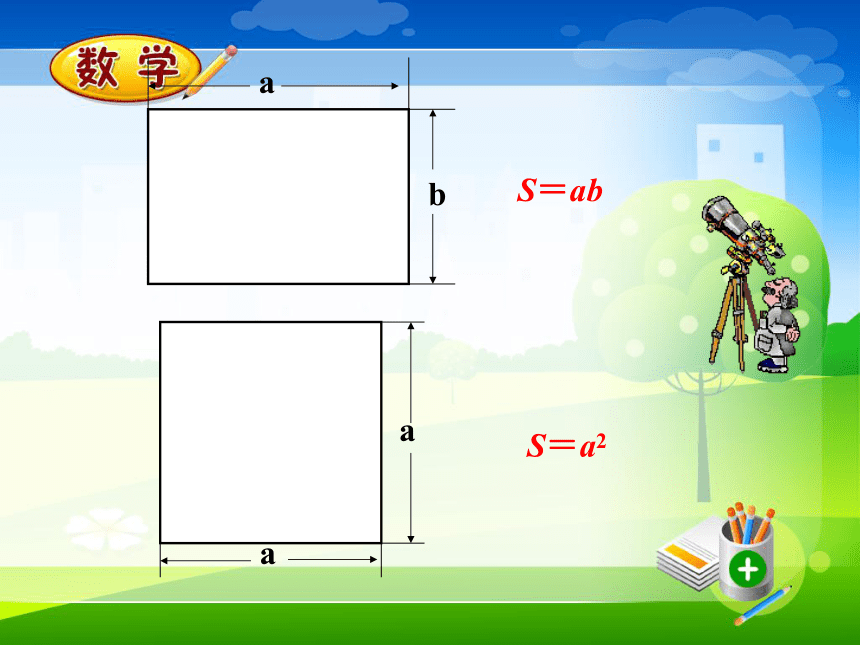
课件48张PPT。想一想:三角形、圆、长方形、正方形的面积公式.S=a2S=ab知识与能力
1.会用含有字母的式子表示数量的关系,理解字母表示数的意义;
2.理解并掌握单项式、多项式的有关概念;
3.能用单项式和多项式表示具体问题中的数量关系.过程与方法
1.在经历字母表示数量关系的过程中,发展符号感.
2.通过观察、类比、归纳得出单项式和多项式概念的数字活动,积累数学活动经验,感觉数学思考过程的条理性.情感态度与价值观
1.通过交流、研讨活动,培养主动与他人合作的意识;
2.通过用含字母的式子描述现实世界中的数量关系,认识到它是解决实际问题的重要数学工具之一.重点
1.单项式的概念;
2.多项式的有关概念.
难点
1.对单项式的系数、次数概念的理解;
2.对多项式的项数、次数概念的理解. 1.边长为m的正方形的周长是_______,面积是_______.
2.一辆汽车的速度是v千米/小时,行驶t小时所走过的路程为_______千米.
3.半径为b的圆的周长为______,面积为________.
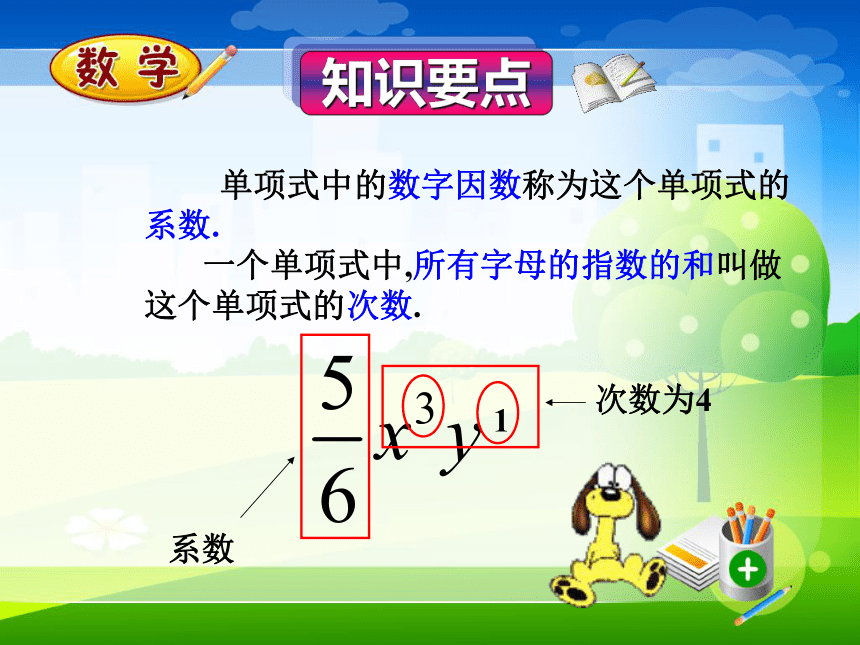
4.设a表示一个数,则它的相反数是_______.4mvt2πb-a填空,并观察式子的特点:m2πb24mvtm2-n数字母v×t-1×n2πbπb2m×m数字母数字母 注意:? 是圆周率的代号,不是字母. 数与字母或字母与字母的乘积像这样的式子叫做单项式. 单项式中的数字因数称为这个单项式的系数.
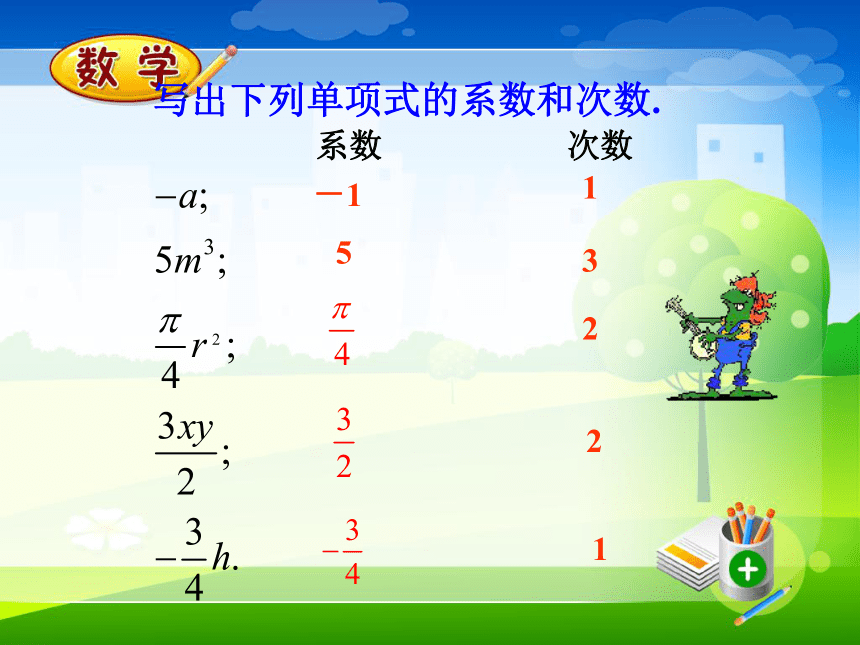
一个单项式中,所有字母的指数的和叫做这个单项式的次数.系数1次数为4 写出下列单项式的系数和次数.系数 次数-1153221 1.数字与字母相乘,乘号省略;
2.表达式中数字写在字母前;
3.数字是带分数一律写成假分数.判断下列说法或书写是否正确. 例:用单项式填空,并指出它们的系数和次数. (1)一个长方形的长是a,宽是b,则它的面积是_______;
(2)一个圆柱的底面的半径是r,高是h,则它的体积是__________;
(3)汽车每秒行驶m千米,1分钟后能行驶多少_____千米;
(4)因金融危机,某商场降价处理产品.一台冰箱原价是a元,现按原价的7.5折出售,这台冰箱现在的售价是________元.
(5)一本书的价格是a元,一块手表的价格是它的7.5倍,则钢笔的价格是______.ab60m7.5a7.5aab60m7.5a7.5a12π36017.57.511同一单项式可以表示不同的含义.-42-16524π 注意:当单项式的系数为1或 –1时,这个“1”应省略不写.关于单项式的系数 1.当单项式的系数是1或-1时,“1”通常省略不写;
2.圆周率π是常数;
3.当单项式的系数是带分数时,通常写成假分数;
4.单项式的系数应包括它前面的性质符号.单项式的次数 1.在一个单项式中,所有字母的指数的和才叫做单项式的次数;
2.单独一个数的次数记为0. (2)、(3)、(4)、(6) 、(7)是单项式.判断下列式子中哪些是单项式?单项式的注意点1.单独一个数或一个字母也叫单项式.2.单独一个非零数的次数是0. 3.单项式的系数包含符号,当系数为1或—1时,这个“1”应省略不写.比如 -2,0,a, l等都是单项式. 5的次数是0; 00是没意义的.如:-n.填空,并观察式子的特点. (1)一个长方形的长为a,宽为b,高为h,则这个长方体的表面积为_____________________.
(2)如图,环形的面积为________________.2ab+2ah+2bh (3)一个数比x的5倍小4,则这个数是
________________.
(4)如图,门的面积为
____________________.5x-42ab+2ah+2bh5x-4单项式的和 观察下面这些式子有什么特点. 几个单项式的和叫做多项式. 在多项式中,每个单项式叫做这个多项式的项.注意:指出每一项时必须包含前面的符号.2ab+2ah+2bh5x-42ab、2ah、2bh5x、-4三项式二项式二项式二项式 下列多项式是哪些单项式的和?常数项
多项式里不含字母的项.指出下列多项式中的常数项. 说出下列多项式是几项式,及其各项分别是什么?多项式的次数
多项式里次数最高项的次数,就是这个多项式的次数.2ab+2ah+2bh5x-42212指出下列多项式的次数. 次 项式三 六次 项式二三注意:几次几项式的数字要大写.1.请说出下列多项式是几次几项式?次 项式三四用多项式填空,并说出它们的项和次数. (1)已知一个二位数的个位数字是m,十位数字是n.用关于m和n的式子表示这个二位数 _____________.
(2)图中阴影部分的面
积是___________.10n+ma2-b2 (3) 每升高1千米,气温下降 -6℃.已知山脚下的气温为16 ℃,那么登高h千米后,气温为(__________ )℃.
(4)下图中阴影部分的面积为___________.16-6h10n+ma2-b216-6h10n、ma2、-b216、-6h12212.填空.五次二项式六次二项式五次四项式 例:某人从甲地到乙地,去时顺风,回来时逆风.如果已知风速时2千米/时,那么他往返的速度分别怎样表示?如果甲乙两个人在无风中时速度分别是20千米/时,25千米/时,则他们在顺风中和逆风中的速度各是多少?解:设在无风时行驶速度为v千米/时,则:
顺风行驶的速度为:( v+2)千米/时;
逆风行驶的速度为:( v-2)千米/时;若甲在无风时的速度为20千米/时,即v=20,
则: v+2=20+2=22;
v-2=20-2=18.
若甲在无风时的速度为25千米/时,即v=25,
则: v+2=25+2=27;
v-2=27-2=23.
由上可知,甲在顺风时的速度为22千米/时,逆风时的速度为18千米/时;乙在顺风时的速度为27千米/时,逆风时的速度为23千米/时.单项式和多项式统称为整式.整式单项式多项式5a,-3m23x+2,xy-6y3整式单项式多项式系数:单项式中的数字因数
次数:所有字母的指数的和项:多项式中的每个单项式
次数:多项式里次数最高项的次数 1. 单项式-m3n 的系数是_______,次数是______, m5n3是____次单项式.
2. 多项式3x2+6y-2z是单项_____,______,
________的和,它是___次___项式.
3. 多项式4m2-5m-7+m3的常数项是____,一次项是_____, 二次项的系数是_____.
4. 如果 -3xym-2 为6次单项式, 则m=____.-1483x26y-2z二三-7-5475.下列说法中,正确的是( )D 6.如果-axyb是关于x的单项式,且系数为2,次数为3,则a,b分别是多少?解:由题意可得:
-a=2,
1+b=3.
得:a=-2,
b=2.
答:a为-2,b为2.3.-15ab-1524a2b244322434x2-310.17a,20a,23a,…,(3n+2)a.
11.S=3n-3,当n=5,7,11时,S=12,
18,30.
1.会用含有字母的式子表示数量的关系,理解字母表示数的意义;
2.理解并掌握单项式、多项式的有关概念;
3.能用单项式和多项式表示具体问题中的数量关系.过程与方法
1.在经历字母表示数量关系的过程中,发展符号感.
2.通过观察、类比、归纳得出单项式和多项式概念的数字活动,积累数学活动经验,感觉数学思考过程的条理性.情感态度与价值观
1.通过交流、研讨活动,培养主动与他人合作的意识;
2.通过用含字母的式子描述现实世界中的数量关系,认识到它是解决实际问题的重要数学工具之一.重点
1.单项式的概念;
2.多项式的有关概念.
难点
1.对单项式的系数、次数概念的理解;
2.对多项式的项数、次数概念的理解. 1.边长为m的正方形的周长是_______,面积是_______.
2.一辆汽车的速度是v千米/小时,行驶t小时所走过的路程为_______千米.
3.半径为b的圆的周长为______,面积为________.
4.设a表示一个数,则它的相反数是_______.4mvt2πb-a填空,并观察式子的特点:m2πb24mvtm2-n数字母v×t-1×n2πbπb2m×m数字母数字母 注意:? 是圆周率的代号,不是字母. 数与字母或字母与字母的乘积像这样的式子叫做单项式. 单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.系数1次数为4 写出下列单项式的系数和次数.系数 次数-1153221 1.数字与字母相乘,乘号省略;
2.表达式中数字写在字母前;
3.数字是带分数一律写成假分数.判断下列说法或书写是否正确. 例:用单项式填空,并指出它们的系数和次数. (1)一个长方形的长是a,宽是b,则它的面积是_______;
(2)一个圆柱的底面的半径是r,高是h,则它的体积是__________;
(3)汽车每秒行驶m千米,1分钟后能行驶多少_____千米;
(4)因金融危机,某商场降价处理产品.一台冰箱原价是a元,现按原价的7.5折出售,这台冰箱现在的售价是________元.
(5)一本书的价格是a元,一块手表的价格是它的7.5倍,则钢笔的价格是______.ab60m7.5a7.5aab60m7.5a7.5a12π36017.57.511同一单项式可以表示不同的含义.-42-16524π 注意:当单项式的系数为1或 –1时,这个“1”应省略不写.关于单项式的系数 1.当单项式的系数是1或-1时,“1”通常省略不写;
2.圆周率π是常数;
3.当单项式的系数是带分数时,通常写成假分数;
4.单项式的系数应包括它前面的性质符号.单项式的次数 1.在一个单项式中,所有字母的指数的和才叫做单项式的次数;
2.单独一个数的次数记为0. (2)、(3)、(4)、(6) 、(7)是单项式.判断下列式子中哪些是单项式?单项式的注意点1.单独一个数或一个字母也叫单项式.2.单独一个非零数的次数是0. 3.单项式的系数包含符号,当系数为1或—1时,这个“1”应省略不写.比如 -2,0,a, l等都是单项式. 5的次数是0; 00是没意义的.如:-n.填空,并观察式子的特点. (1)一个长方形的长为a,宽为b,高为h,则这个长方体的表面积为_____________________.
(2)如图,环形的面积为________________.2ab+2ah+2bh (3)一个数比x的5倍小4,则这个数是
________________.
(4)如图,门的面积为
____________________.5x-42ab+2ah+2bh5x-4单项式的和 观察下面这些式子有什么特点. 几个单项式的和叫做多项式. 在多项式中,每个单项式叫做这个多项式的项.注意:指出每一项时必须包含前面的符号.2ab+2ah+2bh5x-42ab、2ah、2bh5x、-4三项式二项式二项式二项式 下列多项式是哪些单项式的和?常数项
多项式里不含字母的项.指出下列多项式中的常数项. 说出下列多项式是几项式,及其各项分别是什么?多项式的次数
多项式里次数最高项的次数,就是这个多项式的次数.2ab+2ah+2bh5x-42212指出下列多项式的次数. 次 项式三 六次 项式二三注意:几次几项式的数字要大写.1.请说出下列多项式是几次几项式?次 项式三四用多项式填空,并说出它们的项和次数. (1)已知一个二位数的个位数字是m,十位数字是n.用关于m和n的式子表示这个二位数 _____________.
(2)图中阴影部分的面
积是___________.10n+ma2-b2 (3) 每升高1千米,气温下降 -6℃.已知山脚下的气温为16 ℃,那么登高h千米后,气温为(__________ )℃.
(4)下图中阴影部分的面积为___________.16-6h10n+ma2-b216-6h10n、ma2、-b216、-6h12212.填空.五次二项式六次二项式五次四项式 例:某人从甲地到乙地,去时顺风,回来时逆风.如果已知风速时2千米/时,那么他往返的速度分别怎样表示?如果甲乙两个人在无风中时速度分别是20千米/时,25千米/时,则他们在顺风中和逆风中的速度各是多少?解:设在无风时行驶速度为v千米/时,则:
顺风行驶的速度为:( v+2)千米/时;
逆风行驶的速度为:( v-2)千米/时;若甲在无风时的速度为20千米/时,即v=20,
则: v+2=20+2=22;
v-2=20-2=18.
若甲在无风时的速度为25千米/时,即v=25,
则: v+2=25+2=27;
v-2=27-2=23.
由上可知,甲在顺风时的速度为22千米/时,逆风时的速度为18千米/时;乙在顺风时的速度为27千米/时,逆风时的速度为23千米/时.单项式和多项式统称为整式.整式单项式多项式5a,-3m23x+2,xy-6y3整式单项式多项式系数:单项式中的数字因数
次数:所有字母的指数的和项:多项式中的每个单项式
次数:多项式里次数最高项的次数 1. 单项式-m3n 的系数是_______,次数是______, m5n3是____次单项式.
2. 多项式3x2+6y-2z是单项_____,______,
________的和,它是___次___项式.
3. 多项式4m2-5m-7+m3的常数项是____,一次项是_____, 二次项的系数是_____.
4. 如果 -3xym-2 为6次单项式, 则m=____.-1483x26y-2z二三-7-5475.下列说法中,正确的是( )D 6.如果-axyb是关于x的单项式,且系数为2,次数为3,则a,b分别是多少?解:由题意可得:
-a=2,
1+b=3.
得:a=-2,
b=2.
答:a为-2,b为2.3.-15ab-1524a2b244322434x2-310.17a,20a,23a,…,(3n+2)a.
11.S=3n-3,当n=5,7,11时,S=12,
18,30.
