2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理课时作业 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理课时作业 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 276.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 11:15:55 | ||
图片预览


文档简介
17.2勾股定理的逆定理—2021-2022学年数学人教版八年级下册同步课时作业
1.下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12
2.已知M、N是线段AB上的两点,,,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.将直角三角形的各边长都缩小或扩大同样的倍数后,得到的三角形( )
A.可能是锐角三角形 B.不可能是直角三角形
C.仍然是直角三角形 D.可能是钝角三角形
4.一个三角形的三边长分别为8cm,15cm,17cm,则最短边上的高是( )
A.8 cm B.15 cm C.16 cm D.17 cm
5.如果正整数a,b,c满足等式,那么正整数a,b,c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
A.47 B.62 C.79 D.98
6.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?译文:有一块三角形沙田,三边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
7.甲、乙两艘客轮同时离开港口,航行的速度都是400m/min,甲客轮用15min到达A处,乙客轮用20min到达B处.若A、B两处的直线距离为10000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A.北偏西30°方向 B.南偏西30°方向 C.南偏东60°方向 D.南偏东30°方向
8.已知的边长a,b,c满足,则的形状一定是( )
A.等腰三角形或直角三角形 B.等腰直角三角形
C.等腰三角形 D.直角三角形
9.下列条件:
①,
②,
③,
④,
⑤中,
能确定是直角三角形的有( )
A.2个 B.3个 C.4个 D.5个
10.李老师要做一个直角三角形教具,做好后量得三边长分别是30cm,40cm和50cm,则这个教具____________(填“合格”或“不合格”).
11.如图,每个小正方形的边长都为1,是小正方形的顶点,则________.
12.如图是由6个边长均为1的小正方形组成的网格图,,的顶点均在格点上,则____________.
13.如图,E为AB的中点,于点E,,,,求证:.
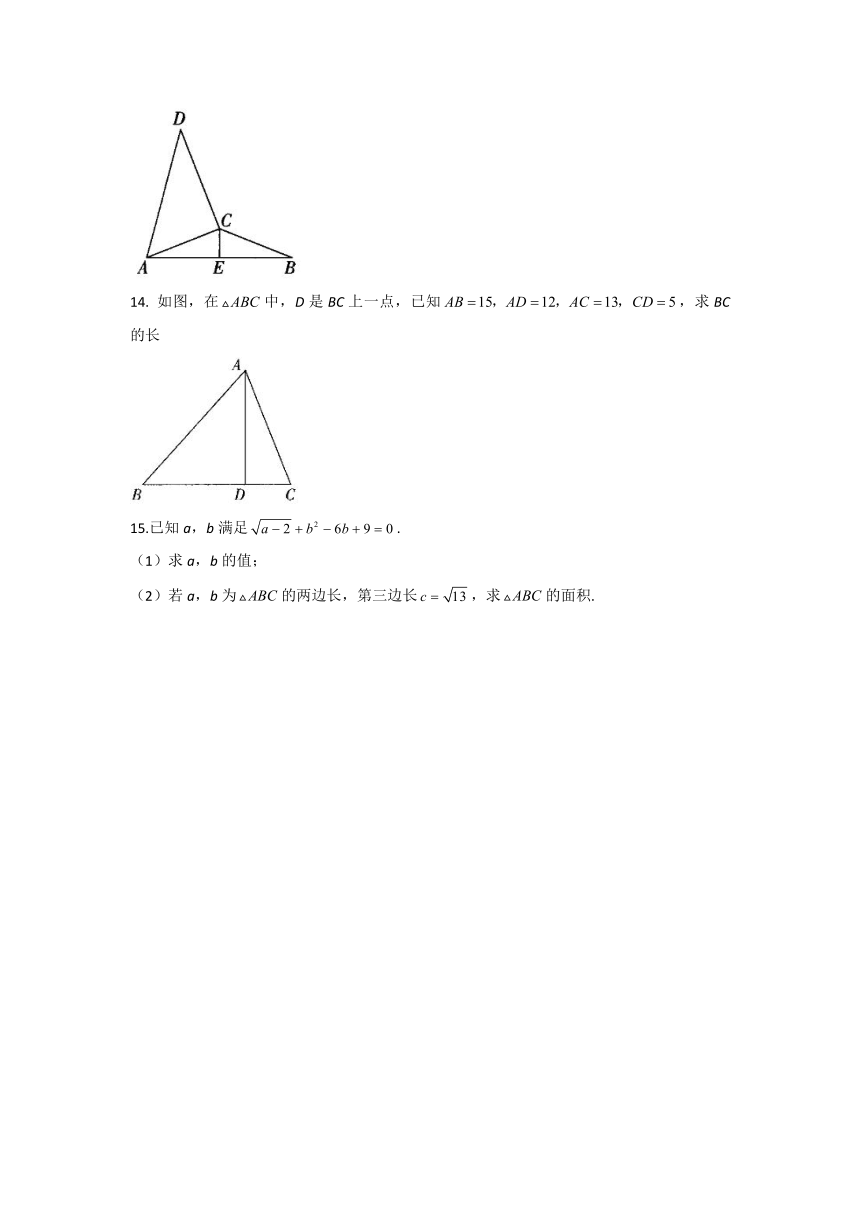
14. 如图,在中,D是BC上一点,已知,求BC的长
15.已知a,b满足.
(1)求a,b的值;
(2)若a,b为的两边长,第三边长,求的面积.
答案以及解析
1.答案:A
解析:A.,能组成直角三角形,故A选项符合题意;B.,不能组成直角三角形,故B选项不符合题意;C.,不能组成直角三角形,故C选项不符合题意;D.,不能组成直角三角形,故D选项不符合题意.故选A.
2.答案:B
解析:如图所示,,,,,是直角三角形,且,故选B.
3.答案:C
解析:设a,b,c是直角三角形的三边长,则.三边长都扩大到原来的n倍后为na,nb,nc,此时,所以以na,nb,nc为三边长的三角形仍然是直角三角形.故选C.
4.答案:B
解析:因为,所以此三角形是直角三角形,且直角边长分别为15cm,8cm,所以最短边上的高是15cm.故选B.
5.答案:C
解析:由题可得,,,…,,,,当时,,,,,故选C.
6.答案:A
解析:将里换算为米,则三角形沙田的三边长分别为2.5千米,6千米,6.5千米.因为,所以该三角形沙田为直角三角形,且直角边长分别为2.5千米和6千米,所以(平方千米).故选A.
7.答案:C
解析:由题意可得甲客轮航行的路程为(m),乙客轮航行的路程为(m),,甲、乙两艘客轮的航行路线呈垂直关系,甲客轮沿着北偏东30°的方向航行,乙客轮的航行方向可能是南偏东60°方向或北偏西60°方向.故选C.
8.答案:A
解析:,
或,或,
为等腰三角形或直角三角形.故选A.
9.答案:C
解析:①时,,是直角三角形;②,是直角三角形;③,设,,,,是直角三角形;④时,,是锐角三角形;⑤,,是直角三角形.故能确定是直角三角形的有4个.故选C.
10.答案:合格
解析:,三边长分别为30cm,40cm和50cm的三角形是直角三角形,这个教具合格.
11.答案:45
解析:连接.
根据勾股定理可以得到,∵,即,∴是等腰直角三角形,∴.
12.答案:45°
解析:如答图,由勾股定理,得,,,所以,所以是直角三角形,且.又因为,所以是等腰直角三角形,所以.利用SAS可证,所以,所以.
13.答案:证明:E为AB的中点,于点E,
,
,,
又,,
,
.
14.
解析:,
即为直角三角形,且,.
,
15. 答案:(1)整理得,,
所以,,
解得,.
(2),,
,
是直角三角形,,
的面积.
1.下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12
2.已知M、N是线段AB上的两点,,,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.将直角三角形的各边长都缩小或扩大同样的倍数后,得到的三角形( )
A.可能是锐角三角形 B.不可能是直角三角形
C.仍然是直角三角形 D.可能是钝角三角形
4.一个三角形的三边长分别为8cm,15cm,17cm,则最短边上的高是( )
A.8 cm B.15 cm C.16 cm D.17 cm
5.如果正整数a,b,c满足等式,那么正整数a,b,c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
A.47 B.62 C.79 D.98
6.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?译文:有一块三角形沙田,三边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
7.甲、乙两艘客轮同时离开港口,航行的速度都是400m/min,甲客轮用15min到达A处,乙客轮用20min到达B处.若A、B两处的直线距离为10000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A.北偏西30°方向 B.南偏西30°方向 C.南偏东60°方向 D.南偏东30°方向
8.已知的边长a,b,c满足,则的形状一定是( )
A.等腰三角形或直角三角形 B.等腰直角三角形
C.等腰三角形 D.直角三角形
9.下列条件:
①,
②,
③,
④,
⑤中,
能确定是直角三角形的有( )
A.2个 B.3个 C.4个 D.5个
10.李老师要做一个直角三角形教具,做好后量得三边长分别是30cm,40cm和50cm,则这个教具____________(填“合格”或“不合格”).
11.如图,每个小正方形的边长都为1,是小正方形的顶点,则________.
12.如图是由6个边长均为1的小正方形组成的网格图,,的顶点均在格点上,则____________.
13.如图,E为AB的中点,于点E,,,,求证:.
14. 如图,在中,D是BC上一点,已知,求BC的长
15.已知a,b满足.
(1)求a,b的值;
(2)若a,b为的两边长,第三边长,求的面积.
答案以及解析
1.答案:A
解析:A.,能组成直角三角形,故A选项符合题意;B.,不能组成直角三角形,故B选项不符合题意;C.,不能组成直角三角形,故C选项不符合题意;D.,不能组成直角三角形,故D选项不符合题意.故选A.
2.答案:B
解析:如图所示,,,,,是直角三角形,且,故选B.
3.答案:C
解析:设a,b,c是直角三角形的三边长,则.三边长都扩大到原来的n倍后为na,nb,nc,此时,所以以na,nb,nc为三边长的三角形仍然是直角三角形.故选C.
4.答案:B
解析:因为,所以此三角形是直角三角形,且直角边长分别为15cm,8cm,所以最短边上的高是15cm.故选B.
5.答案:C
解析:由题可得,,,…,,,,当时,,,,,故选C.
6.答案:A
解析:将里换算为米,则三角形沙田的三边长分别为2.5千米,6千米,6.5千米.因为,所以该三角形沙田为直角三角形,且直角边长分别为2.5千米和6千米,所以(平方千米).故选A.
7.答案:C
解析:由题意可得甲客轮航行的路程为(m),乙客轮航行的路程为(m),,甲、乙两艘客轮的航行路线呈垂直关系,甲客轮沿着北偏东30°的方向航行,乙客轮的航行方向可能是南偏东60°方向或北偏西60°方向.故选C.
8.答案:A
解析:,
或,或,
为等腰三角形或直角三角形.故选A.
9.答案:C
解析:①时,,是直角三角形;②,是直角三角形;③,设,,,,是直角三角形;④时,,是锐角三角形;⑤,,是直角三角形.故能确定是直角三角形的有4个.故选C.
10.答案:合格
解析:,三边长分别为30cm,40cm和50cm的三角形是直角三角形,这个教具合格.
11.答案:45
解析:连接.
根据勾股定理可以得到,∵,即,∴是等腰直角三角形,∴.
12.答案:45°
解析:如答图,由勾股定理,得,,,所以,所以是直角三角形,且.又因为,所以是等腰直角三角形,所以.利用SAS可证,所以,所以.
13.答案:证明:E为AB的中点,于点E,
,
,,
又,,
,
.
14.
解析:,
即为直角三角形,且,.
,
15. 答案:(1)整理得,,
所以,,
解得,.
(2),,
,
是直角三角形,,
的面积.
