华东师大版八年级下册数学16.2.1 分式的乘除(共17张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学16.2.1 分式的乘除(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 794.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:37:08 | ||
图片预览




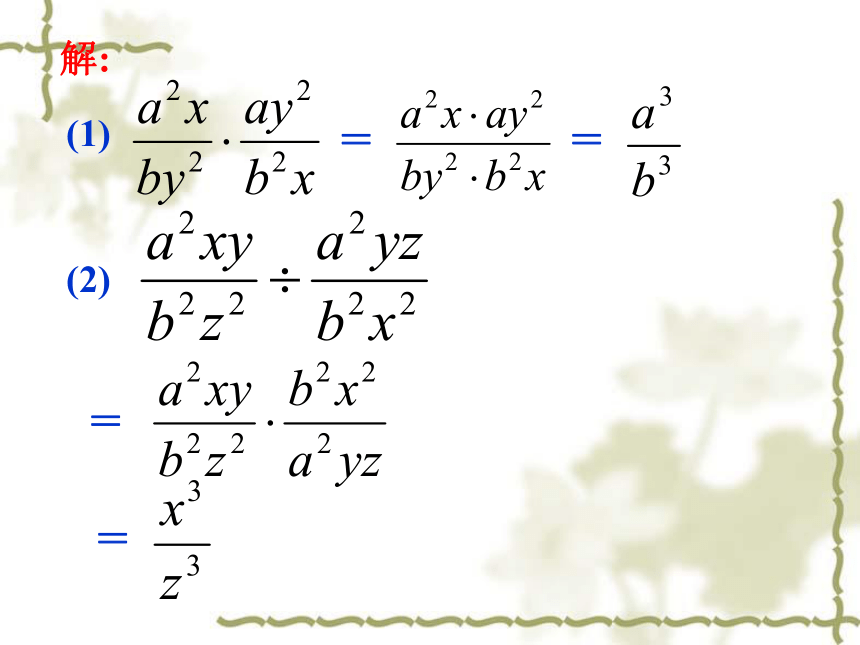
文档简介
(共17张PPT)
课首
约分的基本步骤:
(1)若分子﹑分母都是单项式,则约去分子、分母的公因式;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母的公因式.
约分的依据是分式的基本性质
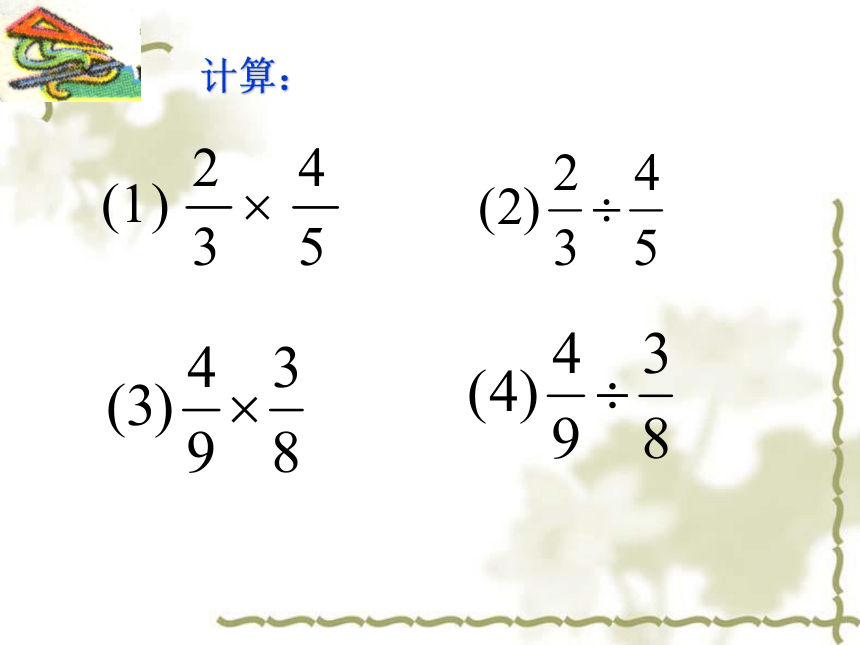
计算:
b
a
d
c
·
=
b
a
=
(2)
(1)
=
bd
ac
÷
d
c
b
a
·
c
d
bc
ad
分数乘分数,用分子的积做积的分子,分母的积做积的分母;分数除以分数,把除式的分子、分母颠倒位置后,与被除式相乘.
你会用语言叙述一下吗?
1.你还记得分数的乘除法则:
这里abcd都是整数,bcd都不为零
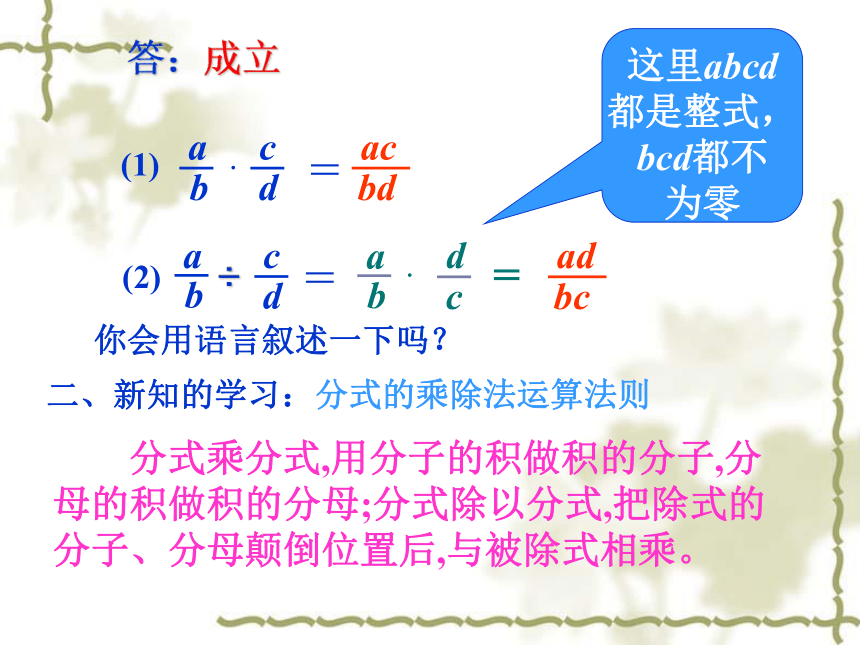
如果让这里的分数换成分式,这个结论还成立吗?
b
a
d
c
·
=
b
a
=
(2)
(1)
=
bd
ac
÷
d
c
b
a
·
c
d
bc
ad
你会用语言叙述一下吗?
分式乘分式,用分子的积做积的分子,分母的积做积的分母;分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
二、新知的学习:分式的乘除法运算法则
答:成立
这里abcd都是整式,bcd都不为零
例1.计算
(1)
(2)
解:
(1)
=
=
(2)
=
=
三、学以致用
学数学是为了用数学解决问题,看看你会用了吗?
(1)你会利用分式的乘除法运算法则计算下列各式吗?
注意:计算结果要化为最简分式或整式
补充 计算(1)
补充 计算(2)
做一做
(3)、
想一想,做一做
k个(k为正整数)
归纳:分式的乘方法则:
分式的乘方是把分式的分子、分母各自乘方,再把所得的幂相除。
公式表示为:
(k为正整数)
看看你会用上面的公式吗?
计算:
补充作业:计算
课堂小结
1、怎样进行分式的乘除法?
2、怎样进行分式的乘方?
小结:
1、分式的乘、除法的法则;
2、运用法则时注意符号的变化;
3、注意因式分解在分式乘除法中的运用;
4、分式乘除的结果要化为最简分式或整式。
课首
约分的基本步骤:
(1)若分子﹑分母都是单项式,则约去分子、分母的公因式;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母的公因式.
约分的依据是分式的基本性质
计算:
b
a
d
c
·
=
b
a
=
(2)
(1)
=
bd
ac
÷
d
c
b
a
·
c
d
bc
ad
分数乘分数,用分子的积做积的分子,分母的积做积的分母;分数除以分数,把除式的分子、分母颠倒位置后,与被除式相乘.
你会用语言叙述一下吗?
1.你还记得分数的乘除法则:
这里abcd都是整数,bcd都不为零
如果让这里的分数换成分式,这个结论还成立吗?
b
a
d
c
·
=
b
a
=
(2)
(1)
=
bd
ac
÷
d
c
b
a
·
c
d
bc
ad
你会用语言叙述一下吗?
分式乘分式,用分子的积做积的分子,分母的积做积的分母;分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
二、新知的学习:分式的乘除法运算法则
答:成立
这里abcd都是整式,bcd都不为零
例1.计算
(1)
(2)
解:
(1)
=
=
(2)
=
=
三、学以致用
学数学是为了用数学解决问题,看看你会用了吗?
(1)你会利用分式的乘除法运算法则计算下列各式吗?
注意:计算结果要化为最简分式或整式
补充 计算(1)
补充 计算(2)
做一做
(3)、
想一想,做一做
k个(k为正整数)
归纳:分式的乘方法则:
分式的乘方是把分式的分子、分母各自乘方,再把所得的幂相除。
公式表示为:
(k为正整数)
看看你会用上面的公式吗?
计算:
补充作业:计算
课堂小结
1、怎样进行分式的乘除法?
2、怎样进行分式的乘方?
小结:
1、分式的乘、除法的法则;
2、运用法则时注意符号的变化;
3、注意因式分解在分式乘除法中的运用;
4、分式乘除的结果要化为最简分式或整式。
